Расчет зубчатой передачи

4.1.2 Расчет зубчатой передачи

Проектный расчет производится с целью ориентировочного определения модуля. В качестве исходных принимаются следующие данные:

М – крутящий момент на валу ведущего зубчатого колеса, М=20,7 Н∙м;

z₁ – число зубьев ведущего зубчатого колеса, z₁=25;

z₂ – число зубьев ведомого зубчатого колеса, z₂=100;

ψ – коэффициент ширины зуба, принимается ψ=15;

σ – угол наклона зубьев, принимается σ=15.

Ориентировочно, величина модуля определяется по формуле:

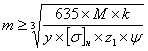. (25)

 (мм).

Принимается ближайшее стандартное значение m=2 мм.

4.1.3 Расчет эталон-вала

Эталон-вал представляет собой коленчатый вал, аналогичный обрабатываемой детали. Предназначен эталон-вал для передачи вращения со шпинделя на зажимные рычаги шатунных шеек. Для обеспечения малого прогиба вал является трехопорным, т.е. статически неопределим. Статическая нагрузка на вал представляет собой сосредоточенные массы рычагов, приложенные в центре каждой шатунной шейки. Дисбаланс вращающихся деталей создает в опорах дополнительные радиальные нагрузки. Эти силы вращаются вместе с валами, создавая в опорах периодически изменяющуюся нагрузку, вызывая колебания. Известно также, что вращение сосредоточенной массы m вокруг оси [6] сопровождается появлением динамической нагрузки. Она стремится разорвать шатунную шейку, увеличивая ее эксцентриситет, поэтому в опасном сечении (соединение коренной и шатунной шеек) возникает продольная динамическая сила:

, (26)

где m – масса рычага, кг, m=40 кг;

w – частота вращения эталон-вала, 1/с, w=13,2 1/с;

r – эксцентриситет, мм, r=40 мм.

 (Н).

Статическая нагрузка:

, (27)

где g – ускорение свободного падения, м/с, g=9,8 м/с.

 (Н).

Уравнение моментов относительно точки А:

, (28)

.

Далее влияние динамических нагрузок в уравнении моментов не учитывается в связи с тем, что они взаимно уравновешиваются, т.к.:

(14+16+18+110)=(11+13+111+113)=752 (мм),

т.е. уравнение моментов выглядит так:

, (29)

где R_A, R_B, R_C – реакции в опорах А, В, С.

Сумма сил, действующих в системе:

, (30)

.

Число неизвестных в двух полученных уравнениях (моментов и сил) превышает число независимых уравнений равновесия, т.е. балка действительно является статически неопределимой. Для решения статически неопределимой системы необходимо составить уравнения перемещений, основанные на отдельном рассмотрении деформаций двух независимых систем – L₁ и L₂:

 (31)

,

где - прогиб опоры В под действием неизвестной нагрузки R_В, не учитывая опору С и нагрузки второй половины эталон-вала (L₂), мм;

 - прогиб опоры В под действием нагрузок Q₁ и Q₂, мм;

 - прогиб опоры В под действием нагрузок , мм;

 - прогиб опоры В под действием неизвестной нагрузки R_В, не учитывая опору А и нагрузки первой половины эталон-вала (L₁), мм;

- прогиб опоры В под действием нагрузок Q₃ и Q₄, мм;

- прогиб опоры В под действием нагрузок , мм.

, (32)

. (33)

Общая формула для определения прогибов балки под действием сил Q и N:

, (34)

где J – осевой момент инерции сечения, мм.

Используя формулы (31), (32), (33), имеем:

 (мм);

 (мм);

 (мм);

 (мм);

 (мм);

 (мм).

Для второй половины эталон-вала:

 (мм);

 (мм);

 (мм);

 (мм);

 (мм);

 (мм).

Таким образом, получаем:

 (мм);

 (мм);

 (мм);

 (мм).

Сложив имеющиеся уравнения (31) и выразив нагрузку R_В, получим:

, (35)

 (Н).

Используя уравнение (29), имеем:

, (36)

 (Н).

Используя уравнение (30), получаем:

, (37)

 (Н).

Изгибающий момент в опасном сечении:

, (38)

 (Н∙мм).

Осевой момент сопротивления сечения вычисляем по формуле:

, (39)

 (мм³).

Площадь сечения равна:

, (40)

 (мм²).

Суммарное напряжение в опасном сечении складывается из изгибающего напряжения и динамического напряжения:

, (41)

 (МПа).

Условие прочности:

 (42)

Так как условие прочности 140 МПа > 79,6 МПа выполнено, делаем вывод – эталон-вал является прочным.