Навигация
Математическое моделирование формоизменения заготовки в процессах МИОМ
1.2 Математическое моделирование формоизменения заготовки в процессах МИОМ
Из-за сложности и ресурсоемкости решения задачи электродинамики для определения пондеромоторных сил в работах [21, 36, 40], предложено заменять пондеромоторные силы давлением ИМП:
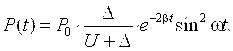 (1.1)
(1.1)
где ![]() =
= ![]() +
+![]() +
+![]() - эквивалентный зазор между индуктором и заготовкой, учитывающий проникновение магнитного поля в металл индуктора
- эквивалентный зазор между индуктором и заготовкой, учитывающий проникновение магнитного поля в металл индуктора ![]() , в металл заготовки
, в металл заготовки ![]() , а также геометрический зазор между индуктором и заготовкой
, а также геометрический зазор между индуктором и заготовкой ![]() ;
; ![]() - текущее перемещение заготовки;
- текущее перемещение заготовки; ![]() - коэффициент затухания;
- коэффициент затухания; ![]() - круговая скорость.
- круговая скорость.
Использование выражения (1.1) позволяет отказаться от совместного решения электромеханических уравнений и свести расчет процессов МИОМ к решению уравнений механики деформируемого твердого тела при заданной внешней нагрузке, параметры которой должны определяться из электрических характеристик системы «установка-индуктор-заготовка». Однако этот подход приводит к большим погрешностям в определении усилий, действующих на индуктор и заготовку и фактически нивелирует разницу между МИОМ и другими высокоскоростными методами, такими как штамповка взрывом, и не отражает основной особенности напряженно-деформированного состояния заготовки, на поверхности которой напряжения равны нулю.
Б.А. Щеглов в работе [53] рассмотрел осесимметричное пластическое течение тонколистовой заготовки из жесткопластического несжимаемого металла, обладающего изотропным упрочнением и вязкостью. Рассмотрен процесс пластического течения трубной заготовки после динамического воздействия. Приводится алгоритм расчета динамических и кинематических параметров процесса. Увеличение вязкости приводит к возрастанию динамических напряжений в заготовке и снижению скоростей деформаций и самих деформаций. Для динамического формоизменения металлов, обладающих большой вязкостью, необходимы более высокие усилия и энергетические затраты.
В работе [25] при раздаче цилиндрических и конических оболочек показано, что величина минимальной напряженности поля при отсутствии его просачивания, для перехода материала в пластическое состояние зависит только от геометрических размеров и механических свойств материала. Напряженное состояние исследовано без учета упрочнения материала и сил инерции.
Задача пластического деформирования тонкостенной конической трубы рассмотрена в работе [43]. В течении времени ![]()
![]() на заготовку действует постоянное равномерное внутреннее давление P , а затем оно снимается и дальнейшее движение происходит за счет накопленной кинетической энергии. Концы трубы свободно опираются по контуру, материал трубы – жесткопластический. Показано, что задача деформировании конической трубы может быть сведена к задаче о деформировании цилиндрической трубы, что и было установлено Е.Г. Ивановым [18].
на заготовку действует постоянное равномерное внутреннее давление P , а затем оно снимается и дальнейшее движение происходит за счет накопленной кинетической энергии. Концы трубы свободно опираются по контуру, материал трубы – жесткопластический. Показано, что задача деформировании конической трубы может быть сведена к задаче о деформировании цилиндрической трубы, что и было установлено Е.Г. Ивановым [18].
Осесимметричная безмоментная раздача конической заготовки ИМП при допущениях малости перемещения вдоль образующей, по сравнению с перемещениями по нормам к поверхности [20], сводится также к задаче о раздаче тонкостенной цилиндрической трубы.
Исследование процессов магнитно-импульсной штамповки значительно усложняется, если в процессе формоизменения образующая заготовки претерпевает изгиб и если поперечное сечение принимает форму отличную от окружности. Экспериментальному исследованию этих процессов посвящен ряд работ [9, 10, 11, 13, 32], к основным результатам которых можно отнести определение технологических возможностей процесса, а также изучение характера течения металла в процессе формоизменения.
Теоретическое исследование этих процессов с позиции механики деформируемого твердого тела было выполнено в работах [6, 16, 23, 30, 32, 35, 54, 55]. Используя экспериментальные данные о характере формоизменения, а также соотношения безмоментной теории оболочек, в работах [30, 32, 54, 55] проведено исследование напряженно-деформируемого состояния в течении процесса формоизменения, определена работа пластического деформирования, обоснован выбор геометрических размеров обрабатываемых деталей и энергия заряда для осуществления операций отбортовки концов труб и т.д.
Приближенный учет изгибающих моментов в процессах МИОМ выполнен в работе [17], при этом условия равенства работ внешних и внутренних сил задачи изгибного деформирования сведены к задачам об одноосном напряженном состоянии. Основным недостатком этой работ является приближенная оценка напряженно-деформированного состояния, возникающего в заготовке.
Использование соотношений моментной теории оболочек к анализу процесса поперечной рифтовки труб дано в работе [6]. В данной постановке задача сводится к решению системы дифференциальных уравнений в частных производных, которая решается методом конечных разностей. Такой подход к анализу динамики тонких упругопластических осесимметричных оболочек был развит в работах [5, 27]. Особенностью данных решений является то, что они применимы только для анализа осесимметричных процессов, для оболочек с плавными очертаниями и требуют создания устойчивых расчетных схем.
Перспективным является использование метода конечного элемента к анализу процессов МИОМ. Присущие ему принципы построения решения позволяют эффективно использовать вычислительную технику при поэтапных исследованиях процессов пластического формоизменения и достаточно просто учитывать геометрическую и физическую неоднородность заготовки, а также неравномерность приложения нагрузки.
В работе [23] предлагается алгоритм исследования переходных процессов деформирования упруго-пластических осесимметричных нетонких оболочек, построенный на основе модифицированного метода конечных элементов [22]. Конечно-элементная дискретизация исследуемой области сводит решение задачи к решению системы дифференциальных уравнений движения, интегрирование которых по времени проводится численно по явной разностной схеме. Такой подход позволяет определить распределение напряжений, деформаций и перемещений в произвольной точке заготовки в любой момент времени. Предложенный алгоритм иллюстрируется на примере решения задачи об отбортовке отверстия в плоской заготовке. Точность полученного решения подтверждается экспериментально. Следует отметить, что упруго-пластический подход наиболее применим к анализу процессов, в которых величина пластических деформаций соизмерима с упругими. В противном случае для уточнения решения используется модель жестко-пластического тела, как это сделано, например, в работе [35], авторы которой использовали метод конечного элемента при исследовании процессов магнитно-импульсной штамповки, протекающих в условиях плоской деформации. В этом случае в качестве искомых функций выступают компоненты узловых скоростей и величины средних напряжений.
Оригинальным является представление узловых скоростей в виде произведения двух функций, одна из которых является функцией времени, постоянной для всей пластической области [33, 49]. Это позволяет отказаться от решения системы дифференциальных уравнений, а свести задачу к системе алгебраических уравнений. Однако использование в данной работе метода множителя Лагранжа для учета условия несжимаемости приводит к трудностям при использовании стандартных приемов при решении систем уравнений, записанных в матричной форме, за счет появления нулей на главной диагонали матрицы системы.
Похожие работы
... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...

0 комментариев