Построение численной модели для задачи электродинамики

2.5 Построение численной модели для задачи электродинамики

2.5.1 Одновитковый индуктор и установка

Для численного интегрирования полученной системы интегро-дифференциальных уравнений (2.27) применялся метод конечных элементов. Были использованы треугольные конечные элементы нулевого порядка, т.е. распределение плотности тока по элементу считалось равномерным. Разбиение индуктора и заготовки на конечные элементы показано на рис. 2.2.

Интегрирование по площади поперечного сечения системы «индуктор‑заготовка» было заменено суммированием интегралов по элементам, вычисляемых по формуле:

,

где - координаты центров масс двух конечных элементов.

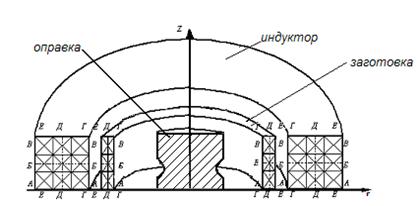
Рис. 2.2.Схема разбиения одновиткового индуктора и заготовки на конечные элементы и обозначение сечений

Для получения уравнений, наиболее близких по форме к уравнениям теории цепей был осуществлен переход от плотностей токов к токам, протекающим по элементу

,

где In – ток, протекающий через сечение элемента n; jn– плотность тока на элементе n; Sn– площадь конечного элемента;

Была получена система линейных дифференциальных по времени уравнений с постоянными коэффициентами. В данном случае конечных элементов нулевого порядка она совпадает с системой, получаемой в рамках метода магнитно-связанных контуров

  (2.33)

где .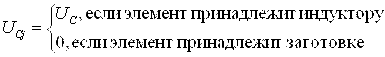

с начальными условиями

В системе уравнений (2.33) приняты следующие обозначения:

,

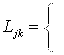
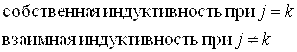— ток в k-м контуре индуктора, - сопротивление j-го контура, — число контуров (элементов) с неизвестными токами, . При  в формуле (2.33) в знаменателе оказывается бесконечность. Однако можно показать, что эта особенность устранима при интегрировании по площади элемента. Диагональные коэффициенты матрицы индуктивностей вычислялись по формуле:

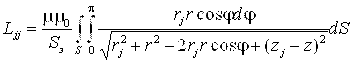 (2.34)

Интегралы по углу и по площади вычислялись по методу Гаусса с 10-ю абсциссами, что обеспечило погрешность порядка 0,5%. Правильность вычисления интегралов подтверждается преобладанием диагональных компонент в матрице индуктивностей и ее положительной определенностью, что гарантирует положительность энергии магнитного поля.

Порядок коэффициентов в левой части уравнения (1) системы уравнений (2.33) составляет 10-7 , а в левой части уравнения (2)- 105. Известно, что численные методы решения систем дифференциальных уравнений весьма чувствительны к такому разбросу величин. Часто это приводит к неустойчивости и плохой сходимости решений, поэтому для улучшения устойчивости было проведено приведение параметров к безразмерному виду по формулам:

После чего система приняла вид:

(2.35)

Интегрирование системы (2.35) велось методом Рунге- Кутта 4-го порядка. Вычисления проводились по формулам:

(2.36)

Для интегрирования системы необходимо на каждом шаге вычислять производные  вектора . Это требует решения системы линейных алгебраических уравнений

 , (2.37)

где,  .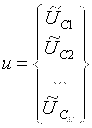

С целью исключить решение на каждом шаге интегрирования системы линейных алгебраических уравнений было осуществлено преобразование (2.37) к виду

,

где – матрица, обратная матрице индуктивностей.

Матрица  вычислялась перед началом интегрирования системы уравнений (2.37) методом исключения Гаусса.

Похожие работы

Технология обработки конструкционных материалов

Скачать

305550

1

104

... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...