Математическая модель электродинамических процессов в одновитковом индукторе

2.2 Математическая модель электродинамических процессов в одновитковом индукторе

Как отмечалось выше, задачу электродинамики для МИОМ можно считать осесимметричной. При этом одновитковый индуктор (или виток) представляется кольцом прямоугольного сечения, а многовитковый - набором таких колец. Так как токи текут исключительно по окружности (следствие осевой симметрии), вектор плотности тока характеризуется только одной компонентой. Тогда можно перейти от векторных уравнений к скалярным, проинтегрировав (2.22) по длине витка индуктора и представив объемный интеграл в виде интеграла по площади и интеграла по контуру и перейдя к цилиндрическим координатам. С учетом того, что

, (2.23)

еще раз проинтегрируем (2.22) по контуру и получим

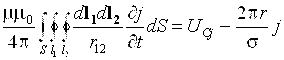 (2.24)

Выражение 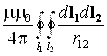 есть ни что иное, как взаимная индуктивность двух элементарных круговых контуров l1 и l2. Перепишем (2.24) с учетом этого

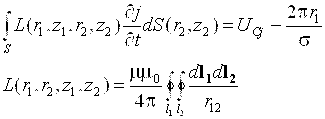, (2.25)

где - плотность тока, – напряжение на конденсаторной батарее, - удельная проводимость,  - емкость конденсаторной батареи,  – общая площадь сечения индуктора и заготовки.

Дополнительно к (2.25) требуется уравнение изменения напряжения на конденсаторе со временем. Оно получается с использованием закона сохранения заряда на пластинах конденсатора и выглядит так:

, (2.26)

где– площадь сечения витка индуктора.

Интегрирование в (2.26) осуществляется по площади сечения витка индуктора. Таким образом, полная система дифференциальных по времени и интегральных по пространству уравнений относительно плотности тока и напряжения на конденсаторе, описывающая электрические процессы в одновитковом индукторе и заготовке, выглядит следующим образом:

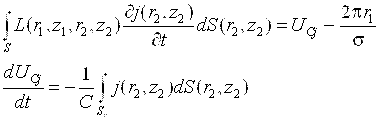(2.27)

Для решения системы (2.27) необходимо задать начальные условия–распределение плотности тока и напряжение на конденсаторной батарее в начальный момент времени:

2.3 Математическая модель электродинамических процессов в многовитковом индукторе

Для обобщения математической модели (2.27) на случай многовиткового индуктора необходимо учесть дополнительно закон сохранения заряда между витками. Интегральная форма приведена ниже

, (2.28)

где – номер витка индуктора, а – площадь витка с номером , S1 – площадь витка под номером один.

Для учета закона сохранения заряда между витками был использован метод множителей Лагранжа, т.к. другие способы приводили к нарушению закона сохранения энергии. Функционал невязки для уравнения (2.27) с учетом дополнительных слагаемых имеет вид:

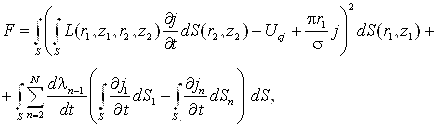 (2.29)

где -множители Лагранжа, а  и -плотности тока в первом и n-м витках.

Дифференциальная по времени форма записи множителей Лагранжа была выбрана для удобства их включения в систему дифференциальных по времени уравнений, получаемую после дискретизации.

2.4 Математическая модель электромеханических процессов в системе «индуктор-заготовка»

Решение задачи механики для индуктора не является целью данной работы, поэтому индуктор будем считать неподвижным. С точки зрения электродинамики индуктор является набором электрически связанных цилиндрических колец, а заготовка – цилиндрической оболочкой. В заготовке отсутствуют другие электрические поля, кроме индуцированных. Поэтому уравнение для распределения плотности тока в заготовке можно получить из уравнения для одновиткового индуктора (2.22), приняв равным 0 напряжение на конденсаторной батарее:

.

Пондеромоторные силы вычислялись как производные от энергии по координате при неизменных токах [31]

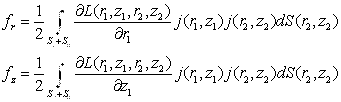(2.30)

где fr, fz – плотности пондеромоторных сил по осям r и z.

Так как структура уравнений для индуктора и заготовки одна и та же, после дискретизации возможно сформировать общую систему уравнений, описывающую изменение распределения плотности тока и напряжения на конденсаторной батарее со временем.

Заготовку будем рассматривать осесимметричную, материал которой, упруго-пластическим.

Рассмотрим малые деформации заготовки. Связь между компонентами деформаций и перемещений в случае осесимметричной деформации имеют вид [50],

.

Будем использовать теорию пластического течения для моделирования поведения заготовки. Основные ее соотношения с учетом малости деформаций приведены в формулах (2.11) – (2.12).

Вариационное уравнение Лагранжа с учетом даламберовых сил инерции и пондеромоторных сил имеет вид [8, 14, 15, 50]:

, (2.31)

где  - плотность материала; - тензоры напряжений и приращений деформаций соответственно, , - векторы ускорений, перемещений, пондеромоторных сил соответственно;  - объем заготовки.

В задаче об осесимметричной деформации, когда состояния по угловой координате  однородны после интегрирования по получим

. (2.32)

Здесь интегрирование ведется по площади  сечения заготовки.

Похожие работы

Технология обработки конструкционных материалов

Скачать

305550

1

104

... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...