Многовитковый индуктор и установка

2.5.2 Многовитковый индуктор и установка

При минимизации функционала невязки (2.29) получили систему уравнений, последующая дискретизация и учет изменения напряжения на батарее конденсаторов приводит к системе линейных дифференциальных уравнений первого порядка с постоянными коэффициентами:

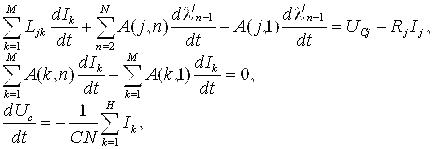(2.38)

где

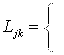
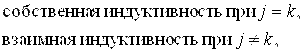
 - ток в k-м контуре индуктора; - сопротивление в j-м контуре; - напряжение в j-м контуре; - текущее напряжение на конденсаторной батарее; N - количество витков; n - номер витка,; k – номер контура; М – число контуров принадлежащих индуктору и заготовке; H - число контуров, принадлежащих индуктору.

В системе уравнений (2.38) первое уравнение отражает закон электромагнитной индукции с учетом множителей Лагранжа, второе – закон сохранение тока, а третье уравнение - закон изменения напряжения на батарее.

Для решения системы уравнения (2.38) использовался метод Рунге-Кутта 4-го порядка (2.36).

2.5.3 Система «индуктор-заготовка-установка»

Система «установка - индуктор – заготовка» описывалась двухконтурной схемой замещения (рис. 2.3).

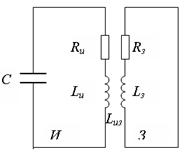
Рис. 2.3. Упрощенная электрическая схема технологической системы МИОМ

Буквами «И» и «З» обозначены соответственно контуры индуктора и заготовки. С - емкость батареи конденсаторов, Rи, Lи, Rз, Lз – сопротивления и собственные индуктивности индуктора и заготовки, Lиз- взаимная индуктивность индуктора и заготовки.

Для учета омического сопротивления установки и ее индуктивности в первое уравнение системы (2.38) введем дополнительные слагаемые, отражающие падение напряжения на токоподводе и дополнительную ЭДС индукции:

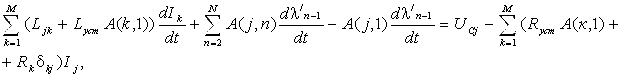(2.39)

где Rуст- сопротивление установки, Lуст- индуктивность установки.

2.5.4 Вычисления сил и температур

На основе известных токов вычислялись силы и температуры в каждой точке сечения индуктора и заготовки.

Выражение для силы взаимодействия между двумя элементами i и j после дискретизации (2.30) имет вид:

.

Тогда выражение для суммарной силы, действующей на элемент, выглядит следующим образом:

.

а выражение для компонентов плотности силы выглядит следующим образом:

, (2.40)

где -площадь i-го элемента.

Ниже приведены выражения для радиальной и осевой компонент силы, с которой элемент действует сам на себя:

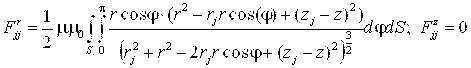
Считалось, что, так как время процесса мало, теплопередача не происходит. Тогда формулы для скорости нагрева и температуры элемента выглядят следующим образом:

; .

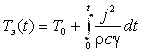2.5.5 Численное моделирование механических процессов в заготовке

Для решения задачи упруго-пластичности применяется метод упругих решений, заключающийся в сведении нелинейной задачи пластичности к сходящейся последовательности задач упругости.

Меридиональное сечение заготовки разбивалось на треугольные конечные элементы, причем сетки подзадач электродинамики и механики совпадали (рис.2.2). После дискретизации получили систему дифференциальных уравнений, описывающую движение узлов одного элемента, когда он находится в упругом состоянии

, (2.41)

где M- матрица масс, K-матрица жесткости задачи упругости; ; - радиальная координата центра масс элемента; F- локальный вектор сил, действующих на элемент, ‑вектор перемещений, B – матрица производных функций формы, D- матрица упругих постоянных.

При построении численной модели использовались основные соотношения теории пластического течения.

1) приращение деформации  на шаге по времени  складывается из приращения упругой  и пластической  деформации:

2) приращение пластической деформации может быть получено по формуле для ассоциированного закона пластического течения:

В данной задаче в качестве условия текучести принят критерий Мизеса

где ,

где  - напряжения в элементе, - предел текучести, Аp - работа пластического формоизменения.

Закон Гука в дискретной форме

(2.44)

после выражения упругих деформаций из (2.42) как разности полных и пластических деформаций можно записать следующим образом

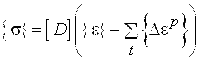. (2.45)

Подставляя данное выражение в соотношения МКЭ для упругой задачи, получим

(2.46)

Учитывая, что  и , упростим выражение (2.39)

, (2.47)

где - приведенная сила, связанная с пластическим формоизменением.

Интегрирование системы дифференциальных уравнений (2.47) проводилось методом дискретизации по времени

(2.48)

где , - значения перемещения, скорости в начале шага; a - ускорения на текущем шаге [42].

После подстановки выражения (2.48) в систему дифференциальных уравнений (2.47) движения получили:

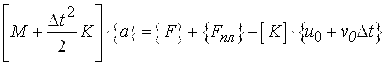.  (2.49)

Выражение (2.49) представляет собой систему линейных алгебраических уравнений относительно вектора ускорений. Подставив найденный вектор ускорений на данном шаге в (2.48), получим перемещение и скорость в конце данного шага интегрирования.

Для приращения приведенной силы была получена формула на основе теории пластического течения. Подставив (2.43) в выражение приведенной силы пластического формоизменения, получим

, (2.50)

где 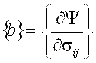- вектор частных производных от уравнения поверхности текучести.

Коэффициент  вычислялся по формуле

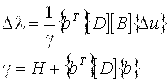, (2.51)

где - вектор приращений узловых перемещений на данном шаге, 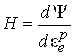 - касательный модуль пластичности.

Соотношения (2.51) можно получить следующим образом. Найдем полное приращение выражения , используя дифференциал

. (2.52)

Когда материал находится в пластическом состоянии выполняется условие текучести, а соответственно выражение (2.52) должно тождественно равняться нулю.

(2.53)

С учетом того, что - приращение работы пластической деформации, преобразуем равенство (2.53)

. (2.54)

Подставим в (2.54) выражение пластических деформаций через ассоциированный закон течения

. (2.55)

Запишем (2.55) в приращениях

(2.56)

и подставим выражение приращения пластической деформации через ассоциированный закон течения

.(2.57)

Подставляя (2.57) в (2.55) и проводя ряд преобразований, получаем (2.44).

Для численного решения задачи необходимо применять итерационную процедуру. Ниже приведен ее алгоритм

1)   вычислить вектор внешних сил, используя решение задачи электродинамики;

2)   взять вектор приведенной силы пластического формоизменения (2.50) с предыдущего шага и вычислить приращение вектора узловых перемещений по формулам (2.48) и (2.49);

3)   используя значения приращения вектора узловых перемещений, вычислить  по формуле (2.51);

4)   откорректировать вектор приведенной силы пластического формоизменения, используя новое значение ;

5)   вычислить уточненное приращение вектора узловых перемещений по формулам (2.48) и (2.49);

6)   оценить погрешность, сравнив приращение перемещений на данном шаге с полученными ранее на предыдущей итерации или (для первой итерации) на шаге 2. Если погрешность превышает заданное значение, перейти к шагу 3.

7)   Откорректировать значение предела текучести с учетом упрочнения.

8)   Если не достигнут конец временного отрезка решения задачи, сделать новый шаг по времени и перейти к шагу 1.

Похожие работы

Технология обработки конструкционных материалов

Скачать

305550

1

104

... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...