Навигация
Математическое моделирование электромеханических процессов при магнитно-импульсной обработки металлов
1.3 Математическое моделирование электромеханических процессов при магнитно-импульсной обработки металлов
В случае переменной величины рабочего зазора, например, в процессе формоизменения заготовки, импульсное магнитное поле в системе «индуктор-заготовка» неоднородно, что резко усложняет расчет его величины и распределения по поверхности заготовки при создании инженерных методик расчета.
Кроме того, изменение размеров заготовки в процессе деформирования ведет к изменению индуктивности системы «индуктор-заготовка» и, следовательно, к изменению частоты тока, а увеличение зазора между индуктором и заготовкой приводит к уменьшению давления. При этом за счет пересечения заготовкой магнитных силовых линий в ней и индукторе возникают дополнительные токи, которые могут оказывают влияние на величину давления ИМП.
Учесть эти факторы можно, если рассматривать процесс магнитно-импульсной обработки как электромеханический, т.е. процесс деформирования описывать системой электрических уравнений, полученных на основе теории цепей, совместно с уравнениями движения [44, 56]. Но так как методы теории цепей позволяют исследовать только интегральные параметры системы, то с их помощью трудно получить достоверную картину напряженно-деформированного состояния индуктора и заготовки, однако, как будет показано ниже, индуктор и заготовку можно представить как совокупность параллельно соединенных контуров с токами и исследовать их силовое взаимодействие друг с другом.
Изучению процессов раздачи и обжима тонкостенных цилиндрических заготовок посвящено большое количество работ [60,14]. Среди этих работ следует отметить работы Иванова Е.Г. [14], который, используя решения безразмерных уравнений движения с широким диапазоном варьирования входных параметров, получил приближенные аналитические выражения, позволяющие судить о степени влияния того или иного параметра на величину деформации заготовки и определять параметры МИУ по заданному формоизменению. Однако следует заметить, что универсальность полученных решений ограничена видом аппроксимирующей кривой ![]() , которая выбрана в виде
, которая выбрана в виде ![]() .
.
Основной недостаток описанных моделей состоит в априорном задании усилий в виде давления, изменяющегося со временем по гармоническому закону, тогда как в действительности индуктор и заготовка находится под действием объемных пондеромоторных сил.
Определенный интерес представляет работа [60], в которой проведен анализ процесса обжима тонкостенной трубной заготовки. Получено приближенное решение и более точное численное решение системы дифференциальных уравнений. Оба метода позволяют провести анализ влияния различных параметров установки, индуктора и заготовки на конечный результат обжима. Из приближенного решения выделены три условия для оптимального расчета процесса, одно из которых - выражение для оптимальной частоты, при которой достигается максимальная деформация. Приведены зависимости для расчета тока в группе конденсаторов и тока, индуцированного в заготовке, давления магнитного поля, частоты разрядного тока. Отмечается удовлетворительное совпадение результатов теоретического и экспериментального исследований.
В работе Батыгина Ю.В., Лавинского В.И. [7] предложен подробный анализ проблем магнитно-импульсной обработки тонкостенных металлических заготовок, толщина которых, как минимум на порядок, меньше эффективности глубины проникновения поля в соответствующую проводящую среду. Также сформированы, обоснованы новые предположения по увеличению эффективности силового воздействия на обрабатываемые объекты при существенной диффузии магнитных полей. Был сделан вывод, что максимальная эффективность магнитно-импульсного воздействия имеет место в случае, когда толщина заготовки много больше глубины проникновения поля.
В работах А.А. Орлова [38] была разработана согласованная по времени математическая модель электромеханических процессов, протекающих индукторе и заготовке при магнитно-импульсной обработки металлов в процессе разряда магнитно-импульсной установки, учитывающая влияние распределения плотности тока в индукторе и заготовке. Оригинальным в этих работах является то, что исследование электродинамических процессов и напряженно-деформированного состояния индуктора и заготовки выполнены на базе метода конечных элементов. При этом формоизменение заготовки описывалось с помощью деформационной теории пластичности с учетом объемного характера пондеромоторных сил, действующих на неё.
1.4 Интенсификация процессов магнитно-импульсной обработки
Одним из путей повышения эффективности работы индукторов является интенсификация процесса МИОМ.
В работах А.К. Талалаева [48] экспериментально показано, что на эффективность процесса магнитно-импульсной обработки существенное влияние оказывает не только количество витков спирали, но и их форма. При этом форма сечения витка должна обеспечивать равномерное распределение импульсного тока по его рабочей поверхности. Выбор оптимальной формы сечения витка производился экспериментально из нескольких вариантов (рис. 1.1).
№1 №2 №3
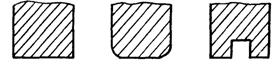
№4 №5 №6
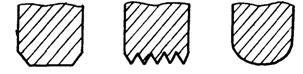
Рис.1.1. Варианты различного исполнения сечения спирали индуктора
Наиболее удачными формами профиля сечения оказались круглая и прямоугольная с закругленными кромками под радиус 1,5-2мм, при которых исключаются острые кромки – концентраторы тока и источники образования усталостных трещин.
Для более равномерного распределения токовых нагрузок на рабочей поверхности индуктора целесообразно выполнять спиральные проточки прямоугольного профиля, глубина которых больше глубины проникновения тока в металл индуктора в 1,5 – 2раза. Количество спиральных проточек зависит от высоты витка. При высоте витка 10-12мм выполняется одна проточка шириной 3-4мм в средней части витка индуктора.
В работах [28, 19] рассмотрен другой подход к данному вопросу, который заключается в нахождении оптимальной частоты разряда магнитно-импульсной установки, при которой достигается максимальное формоизменение заготовки при минимуме энергозатрат. Кроме того, было показано, что существует частота разряда магнитно-импульсной установки при которой предельная степень деформации материала максимальна. Значение этой частоты практически не зависит от механических характеристик материала и схемы напряженного состояния, а зависит от величины декремента затухания: увеличение декремента затухания ведет к увеличению оптимальной частоты и предельной степени деформации, т.е. при деформировании заготовок на высокочастотных установках достигаются большие степени деформации за один переход.
На величину предельной степени деформации при оптимальной частоте разрядного тока оказывают влияние механические свойства материала заготовки, её геометрические размеры и схемы напряженного состояния.
Однако, в этих работах не учитывался объемный характер пондеромоторных сил, действующих на заготовку.
Интенсифицировать процесс обжима также можно за счет управления импульсными магнитными полями.
Существует два самостоятельных метода управления импульсными магнитными полями в процессе магнитно-импульсной штамповки:
1. Управление формой эпюры давления, это возможно при варьировании конструкцией индукторной системы, геометрией её токоведущих секций [19], а также введением специальных экранов [1].
2. Управление формой импульса давление, что возможно при изменении в процессе нагружения параметров разрядного контура [2] или наложении нескольких импульсных полей с различными параметрами [3, 45].
В работе [46] были разработаны методы управления формой импульса давления ИМП в процессе формоизменения детали, путем программируемого дискретного изменения параметров разрядного контура, наложения нескольких полей и наложением токов, позволяющие задавать требуемую кинематику деформационного процесса. Получены расчетные зависимости описывающие форму импульса при программном изменении параметров разрядных контуров.
Численное моделирование показало возможность интенсификации процессов МИОМ при оптимальном программировании и управлении формой импульса давления. Это позволяет в 1,5-2раза повысить точность деталей в режимах упругого соударения с податливой (трансформируемой) оснасткой.
1.5 Выводы по разделу
1. МИОМ – сложный электромагнитно-механический процесс, в котором одновременно протекают и взаимодействуют электрические, магнитные и механические процессы. Поэтому при моделировании этих процессов необходимо учитывать их взаимное влияние друг на друга.
2. При описании формоизменении заготовки, как правило, использовались модели деформационной теории пластичности или теории пластического течения для модели жестко-пластического материала.
3. Отсутствуют научно-обоснованные методики проектирования формы спирали индуктора для реализации процесса обжима с наименьшими энергозатратами.
4. Известные работы по управлению процессом разряда многоблочных магнитно-импульсных установок были направлены на получение заготовок заданной геометрии и обеспечение заданной скорости подхода заготовки к сопрягаемой детали.
1.6 Постановка задачи исследования
Диссертационная работа направлена на решение важной народно-хозяйственной задачи заключающаяся в снижении энергоемкости операций магнитно-импульсной штамповки трубчатых заготовок по схеме обжима путем научно обоснованного выбора геометрии спирали индуктора и управлением процессом разряда магнитно-импульсной установки.
Для решения поставленной задачи необходимо:
1. усовершенствовать математическую модель функционирования «установка-индуктор-заготовка»;
2. исследовать энергосиловые и температурные условия функционирования индукторов различной геометрии;
3. разработать методику проектирования геометрии спирали индуктора, позволяющую наиболее эффективно реализовать процесс обжима трубчатой заготовки;
4. разработать математическую модель функционирования многоблочной магнитно-импульсной установки при неодновременном разряде блоков конденсаторных батарей и обосновать выбор временного интервала включения очередного блока конденсаторных батарей в разрядную цепь;
5. разработать ряд технологических процессов сборки трубчатых заготовок с использованием энергии импульсного магнитного поля.
2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРОМЕХАНИЧЕСКИХ ПРОЦЕССОВ В СИСТЕМЕ «УСТАНОВКА-ИНДУКТОР-ЗАГОТОВКА» ДЛЯ МИОМ
2.1 Основные соотношения электромеханики твердых тел
Принципиальная схема магнитно-импульсной установки приведена на рис.2.1. Через повышающий высоковольтный трансформатор и выпрямитель производят зарядку конденсаторной батареи, состоящей из групп параллельно включенных между собой импульсных конденсаторов. По окончании заряда конденсаторная батарея с помощью специального коммутирующего устройства-разрядника тригатрона разряжается на индуктор, внутри которого размещается заготовка.
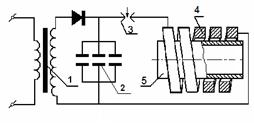
Рис. 2.1. Принципиальная схема МИУ: 1- трансформатор повышающий; 2 - накопитель энергии (батарея конденсаторов);
3 -поджигающие устройства (разрядник); 4 - индуктор;
5 – заготовка
В момент разряда конденсаторной батареи в индукторе протекают импульсные токи, распределенные по сечению весьма неравномерно, соответственно распределены силы и температуры. Их распределение влияет как на деформацию заготовки, так и на прочность и стойкость самого индуктора.
Для учета сложного характера электромеханических процессов, протекающих в системе «установка – индуктор - заготовка», необходимо получить общую систему уравнений, учитывающую взаимное влияние электродинамических и механических процессов.
Далее рассматриваемую систему тел, в которой протекают электромеханические процессы, будем называть электромеханической системой.
Модель электродинамических процессов в электромеханической системе строилась на основе следующих гипотез:
1) токами смещения можно пренебречь по сравнению с токами проводимости;
2) в системе «установка-индуктор-заготовка» отсутствуют ферромагнетики.
3) распределение токов, а, следовательно, объемных сил и температур симметрично относительно оси индуктора. Многовитковый индуктор представляется как набор электрически связанных витков;
4) деформации и перемещения индуктора по сравнению с заготовкой, считаем, малы, поэтому задача механики для индуктора не решаем;
5) заготовку будем считать осесимметричной, а ее материал – упруго-пластическим;
6) время процесса мало, и теплопередача не происходит.
Первое предположение избавляет от необходимости исследования поля в диэлектриках. Оно может быть вычислено через токи, текущие в проводниках. Считается, что все возмущения поля мгновенно распространяются в исследуемой области.
Второе предположение дает возможность исключить влияние пути изменения магнитного поля на свойства материала и таким образом линеаризовать задачу.
Приведенные выше предположения приводят к квазистатической задаче электродинамики. Уравнения Максвелла в этом случае:
| | (2.1) | |
| | (2.2) | |
| | (2.3) | |
| | (2.4) |
где ![]() - вектор магнитной индукции, Тл;
- вектор магнитной индукции, Тл; ![]() - напряженность электрического поля, В/м;
- напряженность электрического поля, В/м; ![]() - напряженность индуцированного электрического поля, В/м;
- напряженность индуцированного электрического поля, В/м; ![]() - плотность тока; m0 - магнитная постоянная; m0=4p×10-7; m - относительная магнитная проницаемость.
- плотность тока; m0 - магнитная постоянная; m0=4p×10-7; m - относительная магнитная проницаемость.
Для замыкания системы необходимо добавить закон Ома с учетом движения среды и напряженности стороннего электрического поля ![]() , создаваемого батареей конденсаторов и закон сохранения заряда:
, создаваемого батареей конденсаторов и закон сохранения заряда:
| | (2.5) | ||
| | (2.6) |
| |
где ![]() - удельная проводимость материала, 1/(Ом×м), а v- cкорость в данной точке и закон сохранения заряда,
- удельная проводимость материала, 1/(Ом×м), а v- cкорость в данной точке и закон сохранения заряда, ![]() -плотность заряда.
-плотность заряда.
Выражение для вектора плотности пондеромоторных сил имеет вид
| | (2.7) |
Для описания движения элементов электромеханической системы в систему уравнений были введены уравнения движения деформируемого твердого тела с учетом гипотезы о малых деформациях:
| | (2.8) | |
| | (2.9) |
где ![]() ,
, ![]() - компоненты симметричных тензоров напряжений и деформаций,
- компоненты симметричных тензоров напряжений и деформаций, ![]() - компоненты вектора перемещений,
- компоненты вектора перемещений, ![]() - компоненты вектора пондеромоторных сил.
- компоненты вектора пондеромоторных сил.
Эти уравнения являются общими как для упругих, так и для упруго-пластических сред.
Для упругой среды связь напряжений и деформаций можно записать в виде
| | (2.10) |
где ![]() - объемный модуль,
- объемный модуль, ![]() - упругий модуль сдвига,
- упругий модуль сдвига, ![]() .
.
А для пластической среды использовать, например, основные соотношения теории пластического течения:
1) Приращение деформации ![]() на шаге по времени складывается из приращения упругой деформации
на шаге по времени складывается из приращения упругой деформации ![]() и пластической
и пластической ![]()
![]() . (2.11)
. (2.11)
2) приращение пластической деформации может быть получено из ассоциированного закона пластического течения
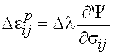 . (2.12)
. (2.12)
В данной задаче в качестве условия текучести принят критерий Мизеса
![]() .
.
Здесь ![]() - напряжения в элементе,
- напряжения в элементе, ![]() - предел текучести, Аp - работа пластического формоизменения.
- предел текучести, Аp - работа пластического формоизменения.
Для описания нагрева проводников при условии адиабатности процесса применимо выражение
| | (2.13) |
где r – плотность материала; с – удельная теплоемкость материала; t - время процесса.
Приведенные выше уравнения достаточны для расчета электромагнитного поля, плотности тока, перемещений, напряжений и деформаций в любой точке исследуемой электромеханической системы, если задать начальные и граничные условия.
Спецификой уравнений Максвелла является то, что выделяют 2 типа граничных условий: условия сшивания полей в разных областях, являющиеся следствием интегральной формы уравнений Максвелла, и граничные условия на бесконечности. Первые выполняются автоматически после перехода от дифференциальных уравнений к интегральным уравнениям относительно потенциалов, а вторые - за счет рассмотрения токов в конечной области.
Граничные условия задачи механики сводятся к заданию на части поверхности Г1 напряжений, а на части Г2 – перемещений:
| | (2.14) |
Начальные условия задают распределения плотности тока ![]() , напряженности стороннего электрического поля
, напряженности стороннего электрического поля ![]() , перемещений
, перемещений ![]() и скоростей
и скоростей ![]() в момент начала процесса:
в момент начала процесса:
|
| (2.15) |
где r – радиус-вектор, u0 - начальное перемещение; v0 - начальная скорость.
В уравнения Максвелла входят параметры электромагнитного поля. Оно существует не только в проводниках, но и в окружающей элементы электромеханической системы среде. Чтобы исключить необходимость рассмотрения поля вне проводников, в системе уравнений электродинамики параметры магнитного поля были выражены через плотность тока. С целью обеспечить тождественное выполнение равенства (2.1), введем векторную функцию ![]() , называемую векторным потенциалом магнитного поля, так что
, называемую векторным потенциалом магнитного поля, так что
| | (2.16) |
Тогда уравнение (2.2) перепишется в виде
|
| (2.17) |
Или, полагая ![]() и m=const,
и m=const,
|
| (2.18) |
где ![]() - оператор Лапласа.
- оператор Лапласа.
Уравнение (2.4) преобразуется следующим образом:
|
| (2.19) |
Решение уравнения (2.18), исчезающее на бесконечности, имеет вид:
|
| (2.20) |
где а, b – радиус-векторы двух произвольных точек, принадлежащих проводникам, V – объем, занимаемый проводниками.
Подставим ![]() и
и ![]() в выражение закона Ома
в выражение закона Ома
|
| (2.21) |
Используя выражение (2.20) и преобразовывая двойное векторное произведение, дифференцируя (2.20) по времени и пренебрегая скоростями, получим
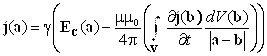
или после преобразований
 (2.22)
(2.22)
Получили интегральное по пространству и дифференциальное по времени уравнение относительно плотности тока. Все дальнейшие уравнения для математической модели электродинамических процессов будут основаны на (2.22).
Похожие работы
... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...
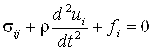
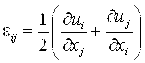 ,
, 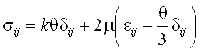 ,
, 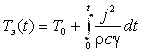 ,
,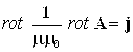 .
.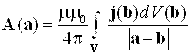 ,
,
0 комментариев