Навигация
ЗАДАЧИ И МЕТОДЫ ЛИНЕЙНОГО ПРГРАММИРОВАНИЯ
1.11. ЗАДАЧИ И МЕТОДЫ ЛИНЕЙНОГО ПРГРАММИРОВАНИЯ.
Дана система m линейно независимых уравнений с неизвестными х ,...,х называемая системой ограничений задачи линейного программирования:
![]() a11x1+...+a1nxn=в1
a11x1+...+a1nxn=в1
(1) ............................
am1x1+...+a1mxn=вn ___
где не уменьшая общности можно считать вi≥0, i=1,m.
Характерной особенностью данной задачи является, то, что число уравнений меньше числа неизвестных, т.е. m<n. Требуется найти неотрицательные значения переменных, которые удовлетворяют уравнениям (1) и обращают в минимум целевую функцию:
(2) q=c1x+...+anx
![]() Более компактно задачи ЛП могут быть записаны в матричной форме:
Более компактно задачи ЛП могут быть записаны в матричной форме:
q(x)=cx=min
(3) Ax=B (B≥0), x≥0
где А - матрица размером m*n, В m - мерный вектор, х и c n - мерные вектора. Матрицу А называют матрицей условий задачи векторов В - вектор ограничений задачи (3).
ГЕОМЕТРИЧЕСКА ИНТЕРПРИТАЦИЯ ОСНОВНОЙ ЗАДАЧИ ПРОГРОММИРОВАНИЯ.
В пространстве Еn множество R1 можно рассматривать как пересечение полупространств (при n=2 - полуплоскостей). ___
(Ax)i≥bi, ( i=1,m)
x≥0 (j=1,n)
СИМПЛЕКС МЕТОД.
1) Идея метода.
Этот метод - это последовательный перебор угловых точек, при которых значение целевой функции убывает от одной угловой точки к другой.
Рассмотрим задачи (каноническую) ЛП:
(4) min<c, x> R0 ={x; Ax=b, x≥0}
x∈R0
Задача (4)-невырожденная, т.е. невырожденна каждая угловая точка ∈R0. Итерационный шаг состоит в переходе от одной угловой точки х круговой точке х', при котором значение целевой функции убывает; <C, x'> < <C, x> x -угловая точка. Базис В образует, первые m столбцов матрицы А. Будем записывать матрицу А=[В,D], где В=[a1, a2,..., am].
D=[an+1, an+2,..., an]
xT=(xвТ, xдТ), CТ=(CвТ, CдТ)
хВ - базис компоненты, хд - в небазисные компоненты.
2) Выбор столбца для ввода в базис.
Известна угловая точка х: хв>0, хд=0, det(В)≠0, Вхв=в
 Рассмотрим векторы: хк=хк(ℷ)= xв-ℷbak-1 ______
Рассмотрим векторы: хк=хк(ℷ)= xв-ℷbak-1 ______
ℷ k=(m+1,n)
0
где ℷ является к - й компонентой вектора х.
Если хв>0, то при малых ℷ>0; хk≥0, т.к. Ахk=в, то хk∈R○ при малых ℷ>0. Кроме того:
<C1 xk>=<C1 x>-ℷ[<Cв, B-1ak>-Ck]=<C, x>-ℷ∆k
∆к - определитель для любого к=1,n, причем при к=1,m;
∆к=<Cв, B-1ak>-Ck=<Cв, Cк>Cк=Cк-Cк=0
Окончательно; <C1 xк>=<C1x>-ℷ∆x (k=1,n)
3)Выбор столбца для ввода из базиса.
В зависимости от значков величины ∆к и (В-1ak); возникает 3 случая. ___
a)Если для любого к=1,n будет ∆к=0, то точка х - оптимальная. _____
б) Если найдется номер к≥m+1 такой, что ∆к>0 и В-1ak≤0, то множество R0 неограниченно и функция <С1х> неограниченна снизу на R0.
в) Пусть найдутся такие к≥m+1 и i≤m, что ∆к>0 и (В-1akа )>0.
4)Конечность метода.
хk - новая угловая точка, причем <C1k>=<C1x>-ℷ0 ∆k < <C1 x>. Из этого следует, что итерационный шаг симплексного метода состоит в таком переходе от базиса а1, а2,..., аs, аs+1, am к базису a1, a2,..., as-1, as+1,..., am, ak при котором целевая функция убывает, а значит, симплексный метод приводит к угловой точке х*, в которой достигает минимума за конечное число итераций.
Стр: 19
[ВЮЮ1]
Стр: 19
[ВЮЮ2]
Стр: 29
[ВЮЮ3]
Стр: 1
[ВЮЮ4]
Похожие работы
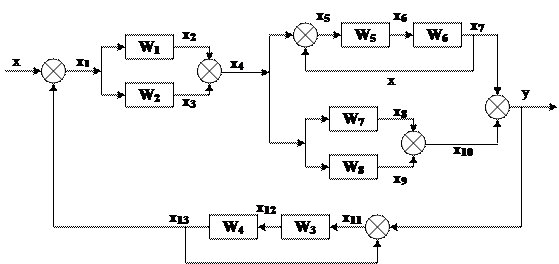
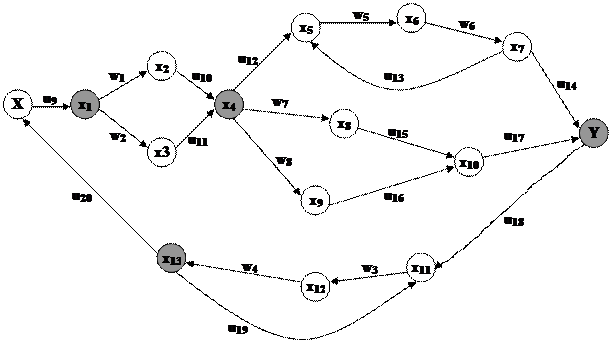
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно. Пример системного подхода ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхэда «Principia Mathematica» (этот фундаметальный трёхтомник математической логики до сих пор не издан на русском языке)[8]. Заключение Прародителем информатики является кибернетика, основанная американским математиком Норбертом Винером, опубликовавшим в 1948 году одноименную книгу. Основоположником ...
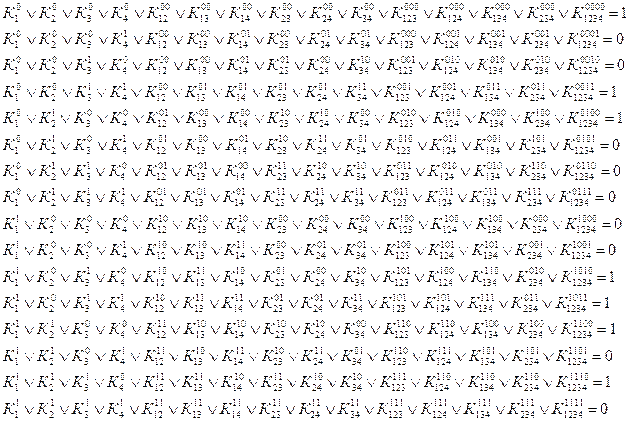
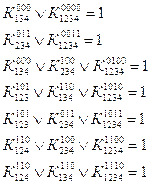
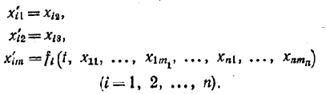

0 комментариев