Основные параметры процесса, несмотря на воздействие возмущения, должны стабилизироваться или изменяться согласно заданию
ПОНЯТИЕ ДИНАМЧЕСКОГО ОБЬЕКТА
ОБЪЕКТЫ УПРАВЛЕНИЯ С НЕПРЕРЫВНЫМ
Если всех t ⌡ A(Ʈ)dƮ и A(t) коммутативны, то
ОБЪЕКТЫ УПРАВЛЕНИЯ С ДИСКРЕТНЫМ ВРЕМЕНЕМ
СТРУКТУРНЫЕ СВОЙСТВА ОБЪЕКТОВ УПРАВЛЕНИЯ
МОДЕЛИ СЛУЧАЙНЫХ СИГНАЛОВ
Сложение случайных функций
ОПТИМИЗАЦИЯ В ТЕОРИИ СИСТЕМ
ЗАДАЧИ И МЕТОДЫ ЛИНЕЙНОГО ПРГРАММИРОВАНИЯ
Навигация
Сложение случайных функций
Математические основы теории систем
96339
знаков
12
таблиц
7
изображений
1. Сложение случайных функций.
Возьмем две случайные функции X(t), Y(t). Пусть известны моменты этих функций до второго порядка включительно:
M[X(t)],M[Y(t)], Kx(t1,t2),Ky(t1,t2) Kxy(t1,t2)
Найдем математическое ожидание случайной функции:
(15) Z(t)=X(t)+Y(t)
В силу линейности операции определения математического ожидания имеем:
(16) M[Z(t)]=M[X(t)]+M[Y(t)]
т.е. математическое ожидание суммы случайных функций равно сумме математических ожиданий этих случайных функций.
Вычитая из равенства (15) равенство (16), получим центрированную случайную функцию:
(17) Z○(t)=X○(t)+Y○(t)
Вычислим корреляционную функцию суммы случайных функций Х(t)+Y(t). По определению корреляционной функции имеем: _____ ____________
(18) Kz(t1, t2)=M[Z○(t1)Z○(t2)]=M[(X○(t1)+Y○(t2)*(X○(t1)+Y○(t2))]=
=Kx(t1, t2)+Kxy(t1, t2)+Kyx(t1, t2)+Ky(t1, t2)
Таким образом, корреляционная функция суммы двух случайных функций равна сумме всех корреляционных и взаимно корреляционных функций этих случайных функций.
2. Дифференцирование случайных функций.
Случайная функция Y(t) называется производной в среднем квадратичном от случайной функции Х(t) по аргументу t, если существует предел:
X○(t+h)-X○(t)
2
(19) lim M -Y○(t) =0
h→0 h
Случайную функцию, для которой существует производная в среднем квадратичном, будем называть дифференцируемой. Случайная функция X(t) называется непрерывной в среднем квадратическом, если существует предел:
(20) lim X(t)=X(t○)
h→0
Корреляционная функция производной dX○(t)/dt=Y○(t) равна:
d2K(t1,t2)
(21) Ky(t1,t2)=
dt1dt2
Взаимная корреляционная функция процесса Х○(t) и его производной равна:
(22) Kxy(t1,t2)=dK(t1,t2)/dt2
Из этих равенств по индукции можно показать справедливость соотношения:
dn+mKx(t1,t2)
(23) Kx(n)x(m)(t1,t2)=
dt1n dt2n
где x(n)(t) и x(m)(t)- соответственно n-я и m-я производные в среднем квадратичном случайной функции Х(t).
3. Интегрирование случайной функции.
Пусть заданы случайная функция Х(Ʈ) и неслучайная функция q(t, Ʈ), где параметр Ʈ изменяется в интервале (а, в). Разобьем интервал (а, в) точками Ʈ○=а,Ʈ○,...,Ʈn=в, на n частей и составим сумму:
n
(24) ∑ X○(Ʈi) q(t,Ʈi)(Ʈi-Ʈi-1)
i=1
значение Ʈi выбрано произвольно в промежуткеƮi-1≤Ʈ≤Ʈi. Рассмотрим предел в среднем квадратическом суммы:
при n→∞ и max[Ʈi-Ʈi-1]→0
n
(25) lim ∑ X○(Ʈi) q(t, Ʈi)(Ʈi-Ʈi-1)
n→∞ i=1
Если этот предел существует, то он называется
интегралом от случайной функции X○(t) в среднем
квадратическом с весом q(t,Ʈ) и обозначается:
b n
(26) Y= ] X○(Ʈ) q(t,Ʈ) dƮ = lim ∑ X○(Ʈi) q(t,Ʈi) ΔƮi
a n→∞ i=1
Рассмотрим случайную функцию Y(t). Согласно определения интеграла от случайной функции получим:
b
(27) Y(t)= ⌡ X(Ʈ) q(t,Ʈ)dƮ
a
Математическое ожидание случайной функции Y(t):
b
(28) M[Y(t)]= ⌡ mx(Ʈ) q(t,Ʈ) dƮ, где mx=M[X(t)]
a
Из неравенства (28) следует, что если существует интеграл, то математическое ожидание интеграла от случайной функции Х(t) равно интегралу от математического ожидания этой случайной функции.
СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ.
Существуют случайные функции, не изменяющие свой характеристики с течением времени. Такие случайные функции называются стационарными.
Случайная функция, для которой все n-мерные функции распределения вероятностей не изменяются с изменением начала отсчета времени, называются стационарными в узком смысле.
Похожие работы
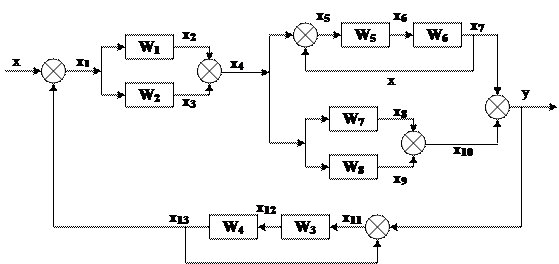
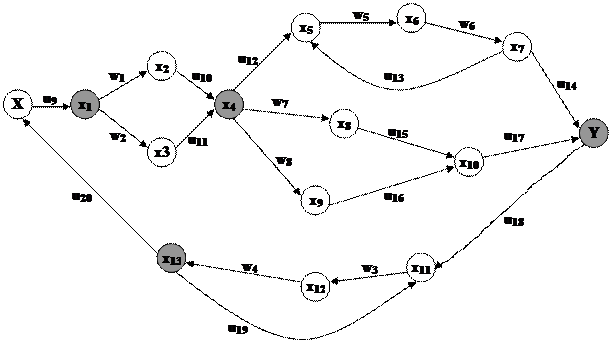
... D=1- W3W4(W1W5W6+ W7+ W1W8+ W2W6 W7+ W2W7+2W2W8+ 1)+ W5W6(W3W4(W7+ W1W5W6+ W2W7+ W2W8+1)-1) Для x1 Для x4 Для y Для х13 Задание 2. Синтез комбинационных схем. 2.1 Определение поставленной задачи Устройство, работа которого может быть представлена на языке алгебры высказываний, принято называть логическим. Пусть такое устройство имеет n ...
... противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно. Пример системного подхода ...
... в момент t, образует пространство выхода системы. Множество всех значений, которые может принять вектор состояния x в момент t, образует пространство состояний системы. 3.3. Описание непрерывных систем с помощью системы дифференциальных уравнений В любой момент времени t состояние системы является функцией начального состояния x(t0) и вектора входа m(t0, t), то есть x(t)=F[x(t0); m(t0; t)], ...
... Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхэда «Principia Mathematica» (этот фундаметальный трёхтомник математической логики до сих пор не издан на русском языке)[8]. Заключение Прародителем информатики является кибернетика, основанная американским математиком Норбертом Винером, опубликовавшим в 1948 году одноименную книгу. Основоположником ...
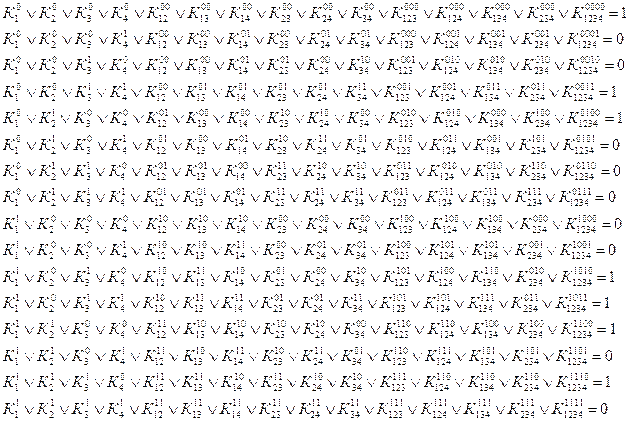
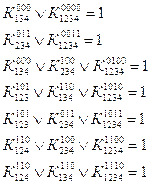
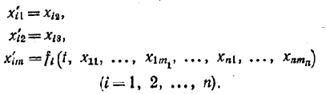
0 комментариев