Понятие информации. Задачи и постулаты прикладной теории информации
Бит = 3,32 бит
Энтропия при непрерывном сообщении
Условная энтропия
Взаимная энтропия
Эффективное кодирование
Энтропия алфавита
Кодирование информации для канала с помехами
Связь корректирующей способности кода с кодовым расстоянием
Понятие качества корректирующего кода
Математическое введение к линейным кодам
Линейный код как пространство линейного векторного пространства
Составление таблицы опознавателей
Определение проверочных равенств
Мажоритарное декодирование групповых кодов
Технические средства кодирования и декодирования для групповых кодов
Построение циклических кодов
Выбор образующего многочлена по заданному объему кода и заданной корректирующей способности
Обнаружение и исправление независимых ошибок произвольной кратности
Технические средства кодирования и декодирования для циклических кодов
Кодирующие устройства
Декодирующие устройства
Навигация
Технические средства кодирования и декодирования для групповых кодов
Теория информации
229704
знака
44
таблицы
52
изображения
4.8.5 Технические средства кодирования и декодирования для групповых кодов
Кодирующее устройство строится на основании совокупности равенств, отражающих правила построения кода. Определение значений символов в каждом из n – k проверочных разрядов в кодирующем устройстве осуществляется посредством сумматоров по модулю два.
На каждый разряд сумматора (кроме первого) используется четыре элемента И (вентиля) и два элемента ИЛИ.
Сумматор по модулю два выпускают в виде отдельного логического элемента, который на схеме изображается прямоугольником с надписью внутри - М2. Приведем несколько примеров реализации кодирующих и декодирующих устройств групповых кодов.
Пример 33. Рассмотрим техническую реализацию кода (7,4), имеющего целью исправление одиночных ошибок.
Правила построения кода определяются равенствами
a1=a3
a5a7,
a2=a3a6a7,
a4=a5a6a7.
Схема кодирующего устройства приведена на рис. 4.6.
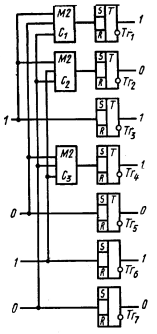
Рис. 4.6.
При поступлении импульса синхронизации со схемы управления подлежащая кодированию k-разрядная комбинация неизбыточного кода переписывается, например, с аналого-кодового преобразователя в информационные разряды n-разрядного регистра. Предположим, что в результате этой операции триггеры регистра установились в состояния, указанные в табл. 4.9.
С некоторой задержкой формируются выходные импульсы сумматоров С1, С2 С3, которые устанавливают триггеры проверочных разрядов в положение 0 или 1 в соответствии с приведенными выше равенствами. Например, в нашем случае ко входам сумматора C1 подводится информация, записанная в 3, 5 и 7-разрядах и, следовательно, триггер Тг1 первого проверочного разряда устанавливается в положение 1, аналогично триггер Тг2 устанавливается в положение 0, а триггер Тг4 — в положение 1.
Сформированная в регистре разрешенная комбинация (табл. 4.10) импульсом, поступающим с блока управления, последовательно или параллельно считывается в линию связи. Далее начинается кодирование следующей комбинации.
Рассмотрим теперь схему декодирования и коррекции ошибок (рис. 4.7), строящуюся на основе совокупности проверочных равенств. Для кода (7, 4) они имеют вид:
a1a3a5a7= 0 ,
a2a3a6a7= 0,
a4a5a6a7= 0 .
| Тr1 | Тr2 | Tr3 | Тr4 | Тr5 | Tr6 | Тr7 |
| — | — | 1 | — | 0 | 1 | 0 |
Кодовая комбинация, возможно содержащая ошибку, поступает на n-разрядный приемный регистр (на рис. 4.7 триггеры Тг1 –Тг7). По окончании переходного процесса в триггерах с блока управления на каждый из сумматоров (C1 – С3) поступает импульс опроса.
Таблица 4.10.
| Тг1 | Тг2 | Тг3 | Тг4 | Тг5 | Tг6 | Тг7 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
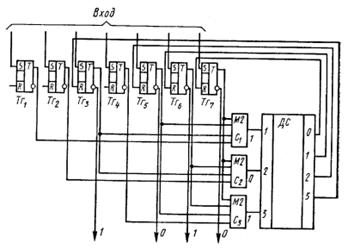
Рис. 4.7.
Выходные импульсы сумматоров устанавливают в положение 0 или 1 триггеры регистра опознавателей. Если проверочные равенства выполняются, все триггеры регистра опознавателей устанавливаются в положение 0, что соответствует отсутствию ошибок. При наличии ошибки в регистр опознавателей запишется опознаватель этого вектора ошибки. Дешифратор ошибки DC ставит в соответствие множеству опознавателей множество векторов ошибок. При опросе выходных вентилей дешифратора сигналы коррекции поступают только на те разряды, в которых вектор ошибки, соответствующий записанному на входе опознавателю, имеет единицы. Сигналы коррекции воздействуют на счетные входы триггеров. Последние изменяют свое состояние, и, таким образом, ошибка исправлена. На триггеры проверочных разрядов импульсы коррекции можно не посылать, если после коррекции информация списывается только с информационных разрядов. Для кода Хэмминга (7,4) любой опознаватель представляет собой двоичное трехразрядное число, равное номеру разряда приемного регистра, в котором записан ошибочный символ.
Предположим, что сформированная ранее в кодирующем устройстве комбинация при передаче исказилась и на приемном регистре была зафиксирована в виде, записанном в табл. 4.11.
Таблица 4.11.
| Тг1 | Тг2 | Тг3 | Тг4 | Тг5 | Тг6 | Tг7 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 |
По результатам опроса сумматоров получаем:
на выходе С1 a1a3a5a7= 1+1+1+0=1,
на выходе С2 a2a3a6a7= 0+1+1+0=0,
на выходе С3 a4a5a6a7= 1+1+1+0=1 .
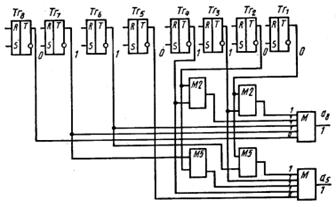
Рис. 4.8.
Следовательно, номер разряда, в котором произошло искажение, 101 или 5. Импульс коррекции поступит на счетный вход триггера Тг5, и ошибка будет исправлена.
Пример 34. Реализуем мажоритарное декодирование для группового кода (8,2), рассчитанного на исправление двойных ошибок.
В случае мажоритарного декодирования сигналы с триггеров приемного регистра поступают непосредственно или после сложения по модулю два в соответствии с уравнениями системы разделённых проверок на мажоритарные элементы М, формирующие скорректированные информационные символы.
Схема декодирования представлена на рис. 4.8. На входах мажоритарных элементов указаны сигналы, соответствующие случаю поступления из канала связи кодовой информации, искаженной в обоих информационных разрядах (5-м и 8-м). Реализуя принцип решения «по большинству», мажоритарные элементы восстанавливают на выходе правильные значения информационных символов.
Похожие работы
... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается используемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...
... , 1968. - 340 с.]. В связи с этим логично было бы далее предположить, что она не предполагает строго количественного эквивалента, подобно энергии или материи. Но парадокс классической теории информации именно в том и состоит, что в её основе лежит предположение Р.Хартли, согласно которому информация допускает количественную оценку [Hartley R.V.L. Transmission of Information // BSTJ.- 1928. - V.7 - ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... с явлениями, которых, может быть, никогда не было и никогда не будет. Память каждого объекта всегда ограничена, а большая часть поступающей информации так и остается невостребованной. При этом общее ее количество (с точки зрения переносящих ее информационных кодов), безусловно, превышает возможности полного ее запоминания. Для предотвращения переполнения памяти и соответственно потери возможности ...
0 комментариев