Навигация
Бит = 3,32 бит
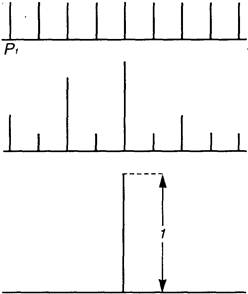
Пример1. Определить количество информации, которое содержится в телевизионном сигнале, соответствующем одному кадру развертки. Пусть в кадре 625 строк, а сигнал, соответствующий одной строке, представляет собой последовательность из 600 случайных по амплитуде импульсов, причем амплитуда импульса может принять любое из 8 значений с шагом в 1 В.
Решение. В рассматриваемом случае длина сообщения, соответствующая одной строке, равна числу случайных по амплитуде импульсов в ней: n = 600.
Количество элементов сообщения (знаков) в одной строке равно числу значений, которое может принять амплитуда импульсов в строке,: m = 8.
Количество информации в одной строке: I = n log m = 600 log 8, а количество информации в кадре: I¢ = 625 I = 625 600 log 8 = 1,125 × 106 бит
Пример2. Определить минимальное число взвешиваний, которое необходимо произвести на равноплечих весах, чтобы среди 27 внешне неотличимых монет найти одну фальшивую, более легкую.
Решение. Так как монеты внешне не отличимые, то они представляют источник с равновероятными состояниями, а общая неопределенность ансамбля, характеризующая его энтропию, поэтому составляет: H1= Iog227 бит.
Одно взвешивание способно прояснить неопределенность ансамбля насчитывающего три возможных исхода (левая чаша весов легче, правая чаша весов легче, весы находятся в равновесии).Так как все исходы равновероятны (нельзя заранее отдать предпочтение одному из них), то результат одного взвешивания представляет источник с равновероятными состояниями, а его энтропия составляет: H2= Iog23 бит.
Так как энтропия отвечает требованию аддитивности и при этом Н1=3Н2= 3 1og23, то для определения фальшивой монеты достаточно произвести три взвешивания.
Алгоритм определения фальшивой монеты следующий. При первом взвешивании на каждую чашку весов кладется по девять монет. Фальшивая монета будет либо среди тех девяти монет, которые оказались легче, либо среди тех, которые не взвешивались, если имело место равновесие. Аналогично, после второго взвешивания число монет, среди которых находится фальшивая монета, сократится до трех. Последнее, третье, взвешивание дает возможность точно указать фальшивую монету.
Рассмотренная выше оценка информации основана на предположении о равновероятности всех знаков алфавита.
В общем случае каждый из знаков появляется в сообщении с различной вероятностью.
Пусть на основании статистического анализа известно, что в сообщении длины n знак xiпоявляется ni раз, т.е. вероятность появления знака:
![]() , (i = 1, 2, 3, ... , m).
, (i = 1, 2, 3, ... , m).
Все знаки алфавита составляют полную систему случайных событий, поэтому:
![]() .
.
Число всех возможных сообщений длины n, в которых знак xiвходит ni раз, где i = 1, 2, 3 ... ,m, определяется как число перестановок с повторениями из n элементов, спецификация которых {n1, n2, ..., nm}. Поэтому количество возможных сообщений определяют по формуле:
![]() .
.
Например, план застройки улицы 10 домами, среди которых 3 дома одного типа, 5 другого и 2 третьего, можно представить
![]() .
.
Количество информации можно найти по формуле:
I = log N = log n! - (log n1!+log n2!+...+log nm!).
Для достаточно больших n это выражение можно преобразовать с помощью приближенной формулы Стирлинга:
log n! » n(ln n - 1).
Воспользовавшись формулой Стирлинга и соотношением![]() , получают:
, получают:
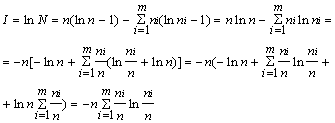
Переходя к вероятностям и произвольным основаниям логарифмов, получают формулы Шеннона для количества информации и энтропии:
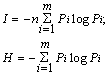
В дальнейшем в выражениях для количества информации I и энтропии H всегда используют логарифмы с основанием 2.
2.1 Свойства энтропии
При равновероятности знаков алфавита Рi = 1/m из формулы Шеннона получают:
![]() .
.
Из этого следует, что при равновероятности знаков алфовита энтропия определяется исключительно числом знаков m алфавита и по существу является характеристикой только алфавита.
Если же знаки алфавита неравновероятны, то алфавит можно рассматривать как дискретную случайную величину, заданную статистическим распределением частот ni появления знаков хi (или вероятностей Рi =ni / n) табл. 2.1:
Таблица 2.1.
| Знаки хi | x1 | x2 | . . . | xm |
| Частоты ni | n1 | n2 | . . . | nm |
Такие распределения получают обычно на основе статистического анализа конкретных типов сообщений (например, русских или английских текстов и т.п.).
Поэтому, если знаки алфавита неравновероятны и хотя формально в выражение для энтропии входят только характеристики алфавита (вероятности появления его знаков), энтропия отражает статистические свойства некоторой совокупности сообщений.
На основании выражения
![]()
![]() ,
,
величину log 1/Pi можно рассматривать как частную энтропию, характеризующую информативность знака хi, а энтропию H - как среднее значение частных энтропий.
Функция (Pi × log Pi) отражает вклад знака хi в энтропию H. При вероятности появления знака Pi=1 эта функция равна нулю, затем возрастает до своего максимума, а при дальнейшем уменьшении Pi стремится к нулю (функция имеет экстремум): рис.2.1.
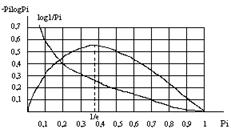
Рис. 2.1. Графики функций log 1/Pi и -Pi × log Pi
Для определения координат максимума этой функции нужно найти производную и приравнять ее к нулю.
Из условия![]() находят: Pi e = 1,где е - основание натурального логарифма.
находят: Pi e = 1,где е - основание натурального логарифма.
Таким образом, функция: (Pi log Pi) при Pi = 1/e = 0,37 имеет максимум: ![]() ., т.е координаты максимума (0,37; 0,531)
., т.е координаты максимума (0,37; 0,531)
Энтропия Н - величина вещественная, неотрицательная и ограниченная, т.е. Н ³ 0 (это свойство следует из того, что такими же качествами обладают все ее слагаемые Pi log 1/Pi).
Энтропия равна нулю, если сообщение известно заранее (в этом случае каждый элемент сообщения замещается некоторым знаком с вероятностью, равной единице, а вероятности остальных знаков равны нулю).
Энтропия максимальна, если все знаки алфавита равновероятны, т.е. Нmax = log m.
Таким образом, степень неопределенности источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. При неравновероятных состояниях свобода выбора источника ограничивается, что должно приводить к уменьшению неопределенности. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния. Действительно, в первом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99), а во втором случае неопределенность максимальна, поскольку никакого обоснованного предположения о результате выбора сделать нельзя. Ясно также, что весьма малое изменение вероятностей состояний вызывает соответственно незначительное изменение неопределенности выбора.
Пример3. Распределение знаков алфавита имеет вид р(х1) = 0,1 р(x2) = 0,1 р(x3) = 0,1 р(x4) = 0,7. Определить число знаков другого алфавита, у которого все знаки равновероятны, а энтропия такая же как и у заданного алфавита.
Особый интерес представляют бинарные сообщения, использующие алфавит из двух знаков: (0,1). При m = 2 сумма вероятностей знаков алфавита: Р1+Р2 = 1. Можно положить Р1 = Р, тогда Р2 = 1-Р.
Энтропию можно определить по формуле:
![]() ,
,
Энтропия бинарных сообщений достигает максимального значения, равного 1 биту, когда знаки алфавита сообщений равновероятны, т.е. при Р = 0,5, и ее график симметричен относительно этого значения.(рис.2.2).
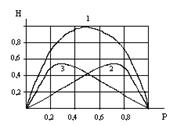
Рис. 2.2. График зависимости энтропии Н двоичных сообщений (1) и ее составляющих (2,3): - (1 - Р) log (1 - P) и - P log P от Р.
Пример 4. Сравнить неопределенность, приходящуюся на букву источника информации (алфавита русского языка), характеризуемого ансамблем, представленным в таблице 2.2, с неопределенностью, которая была бы у того же источника при равновероятном использовании букв.
Таблица 2.2.
| Буква | Вероятность | Буква | Вероятность | Буква | Вероятность | Буква | Вероятность |
| а | 0,064 | й | 0,010 | т | 0,056 | ы | 0,016 |
| б | 0,015 | к | 0,029 | у | 0,021 | э | 0,003 |
| в | 0,039 | л | 0,036 | ф | 0,02 | ю | 0,007 |
| г | 0,014 | м | 0,026 | х | 0,09 | я | 0,019 |
| д | 0,026 | н | 0,056 | ц | 0,04 | пробел | 0,143 |
| е,ё | 0,074 | о | 0,096 | ч | 0,013 | ||
| ж | 0,008 | п | 0,024 | ш | 0,006 | ||
| з | 0,015 | р | 0,041 | ш | 0,003 | ||
| и | 0,064 | с | 0,047 | ъ,ь | 0,015 |
Решение. 1. При одинаковых вероятностях появления любой из всех m = 32 букв алфавита неопределенность, приходящуюся на одну букву, характеризует энтропия
H = log m = log 32 = 5 бит.
2. Энтропию источника, характеризуемого заданным табл. 2.2 ансамблем, находят по формуле:
![]() -0,064 log 0,064 -0,015log0,015 - 0,143log0,143 » 4,43 бит.
-0,064 log 0,064 -0,015log0,015 - 0,143log0,143 » 4,43 бит.
Таким образом, неравномерность распределения вероятностей использования букв снижает энтропию источника с 5 до 4,42 бит
Пример 5. Заданы ансамбли Х и Y двух дискретных величин:
Таблица 2.3.
| Случайные величины хi | 0,5 | 0,7 | 0,9 | 0,3 |
| Вероятности их появления | 0,25 | 0,25 | 0,25 | 0,25 |
Таблица 2.4.
| Случайные величины уj | 5 | 10 | 15 | 8 |
| Вероятности их появления | 0,25 | 0,25 | 0,25 | 0,25 |
Сравнить их энтропии.
Решение. Энтропия не зависит от конкретных значений случайной величины. Так как вероятности их появления в обоих случаях одинаковы, то
Н(Х) = Н(Y) = ![]() - 4(0,25log0,25) = -4(1/4log1/4) =
- 4(0,25log0,25) = -4(1/4log1/4) =
= log 4 = 2 бит
Похожие работы
... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается используемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...
... , 1968. - 340 с.]. В связи с этим логично было бы далее предположить, что она не предполагает строго количественного эквивалента, подобно энергии или материи. Но парадокс классической теории информации именно в том и состоит, что в её основе лежит предположение Р.Хартли, согласно которому информация допускает количественную оценку [Hartley R.V.L. Transmission of Information // BSTJ.- 1928. - V.7 - ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... с явлениями, которых, может быть, никогда не было и никогда не будет. Память каждого объекта всегда ограничена, а большая часть поступающей информации так и остается невостребованной. При этом общее ее количество (с точки зрения переносящих ее информационных кодов), безусловно, превышает возможности полного ее запоминания. Для предотвращения переполнения памяти и соответственно потери возможности ...
0 комментариев