Технические средства кодирования и декодирования для циклических кодов

4.11 Технические средства кодирования и декодирования для циклических кодов

Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1, требуется только наличие связи в схеме. Если коэффициент равен 0, то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.

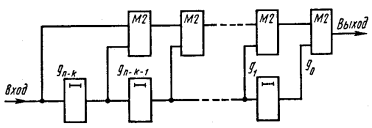
Рис. 4.9.

На рис. 4.9 представлена схема, выполняющая умножение произвольного (например, информационного) многочлена

a(x) = a₀ + a₁x + … + a_k-1x^k-1

на некоторый фиксированный (например, образующий) многочлен

g(x) = g₀ + g₁x + … + g_n-kx^n-k.

Произведение этих многочленов равно

a(x)g(x)=a₀g₀ + (a₀g₁ + a₁g₀)x + … +(a_k-2g_n-k + a_k-1g_n-k-1)x^n-2 +a_k-1g_n-kx^n-1

Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n-k нулей.

На первом такте на вход схемы поступает первый коэффициент а_k-1 многочлена а(х) и на выходе появляется первый коэффициент произведения, равный

a_k-1g_n-k

На следующем такте на выход поступит сумма

a_k-2g_n-k + a_k-1g_n-k-1 ,

т.е. второй коэффициент произведения, и т. д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент а₀g₀

Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 4.10).

На рис. 4.11 представлена схема, выполняющая деление произвольного многочлена, например

a(x)x^m = a₀ + a₁x + … + a_n-1x^n-1

на некоторый фиксированный (например, образующий) многочлен

g(x) = g₀ + g₁x + … + g_n-kx^n-k

Обратные связи регистра соответствуют виду многочлена g(x). Количество включаемых в него сумматоров равно числу отличных от нуля коэффициентов g(x), уменьшенному на единицу. Это объясняется тем, что сумматор сложения коэффициентов старших разрядов многочленов делимого и делителя в регистр не включается, так как результат сложения заранее известен (он равен 0).

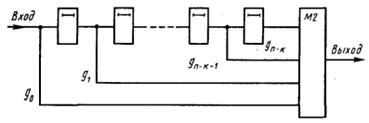
Рис. 4.10.

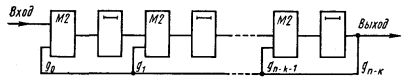
Рис. 4.11.

За первые n-k тактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при х в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени х у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.

Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.

Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n-k, то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевых m-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.

Пример 37. Рассмотрим процесс деления многочлена а(х)х^т =(x³+1)x³ на образующий многочлен g(x) = х³+ х²+1. Схема для этого случая представлена на рис. 4.12, где 1, 2, 3-ячейки регистра. Работа схемы поясняется табл. 4.16.

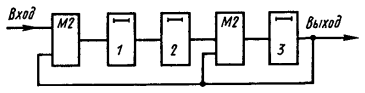
Рис. 4.12.

Вычисление остатка начинается с четвертого такта и заканчивается после седьмого такта. Последующие сдвиги приводят к образованию в регистре последовательности из семи различных ненулевых трехразрядных чисел. В дальнейшем эта последовательность чисел повторяется.

Рассмотренные выше схемы умножения и деления многочленов непосредственно в том виде, в каком они представлены на рис. 4.10, 4.11, в качестве кодирующих устройств циклических кодов на практике не применяются: первая - из-за того, что образующаяся кодовая комбинация в явном виде не содержит информационных символов, а вторая - из-за того, что между информационными и проверочными символами образуется разрыв в n - k разрядов.

Похожие работы

Энтропия. Теория информации

Скачать

63729

48

3

... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается исполь­зуемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...

Классическая теория информации и еe ограничения

Скачать

12754

0

0

... , 1968. - 340 с.]. В связи с этим логично было бы далее предположить, что она не предполагает строго количественного эквивалента, подобно энергии или материи. Но парадокс классической теории информации именно в том и состоит, что в её основе лежит предположение Р.Хартли, согласно которому информация допускает количественную оценку [Hartley R.V.L. Transmission of Information // BSTJ.- 1928. - V.7 - ...

Прикладная теория информации

Скачать

88587

0

39

... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...

Концепции общей теории информации

Скачать

96932

1

1

... с явлениями, которых, может быть, никогда не было и никогда не будет. Память каждого объекта всегда ограничена, а большая часть поступающей информации так и остается невостребованной. При этом общее ее количество (с точки зрения переносящих ее информационных кодов), безусловно, превышает возможности полного ее запоминания. Для предотвращения переполнения памяти и соответственно потери возможности ...