Понятие информации. Задачи и постулаты прикладной теории информации
Бит = 3,32 бит
Энтропия при непрерывном сообщении
Условная энтропия
Взаимная энтропия
Эффективное кодирование
Энтропия алфавита
Кодирование информации для канала с помехами
Связь корректирующей способности кода с кодовым расстоянием
Понятие качества корректирующего кода
Математическое введение к линейным кодам
Линейный код как пространство линейного векторного пространства
Составление таблицы опознавателей
Определение проверочных равенств
Мажоритарное декодирование групповых кодов
Технические средства кодирования и декодирования для групповых кодов
Построение циклических кодов
Выбор образующего многочлена по заданному объему кода и заданной корректирующей способности
Обнаружение и исправление независимых ошибок произвольной кратности
Технические средства кодирования и декодирования для циклических кодов
Кодирующие устройства
Декодирующие устройства
Навигация
Энтропия алфавита
Теория информации
229704
знака
44
таблицы
52
изображения
2. Энтропия алфавита
При кодировании по методу Шеннона - Фано некоторая избыточность в последовательностях символов, как правило, остается (qср > H).
Эту избыточность можно устранить, если перейти к кодированию достаточно большими блоками.
Пример20: Рассмотрим процедуру эффективного кодирования по методике Шеннона - Фано сообщений, образованных с помощью алфавита, состоящего всего из двух знаков x1 и x2 с вероятностями появления соответственно Р(х1) = 0,9; P(x2) = 0,1.
Так как вероятности не равны, то последовательность из таких букв будет обладать избыточностью. Однако, при побуквенном кодировании мы никакого эффекта не получим. Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна
,
т.е. оказывается 
При кодировании блоков, содержащих по две буквы, получим коды:
Таблица 3.4.
| Блоки | Вероятности | Кодовые комбинации | ||
| номер разбиения | ||||
| 1 | 2 | 3 | ||
| x1x1 | 0,81 | 1 | ||
| x1x2 | 0,09 | 0 | 1 | |
| x2x1 | 0,09 | 0 | 0 | 1 |
| x2x2 | 0,01 | 0 | 0 | 0 |
Так как знаки статистически не связаны, вероятности блоков определяют как произведение вероятностей составляющих знаков.
Среднее число символов на блок
а на букву 1,29/2 = 0,645, т.е. приблизилось к Н = 0,47 и таким образом удалось повысить эффективность кодирования.
Кодирование блоков, содержащих по три знака, дает еще больший эффект:
Таблица 3.5.
| Блоки | Вероятность Pi | кодовые комбинации | ||||
| номер разбиения | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| x1x1x1 | 0,729 | 1 | ||||
| x2x1x1 | 0,081 | 0 | 1 | 1 | ||
| x1x2x1 | 0,081 | 0 | 1 | 0 | ||
| x1x1x2 | 0,081 | 0 | 0 | 1 | ||
| x2x2x1 | 0,009 | 0 | 0 | 1 | 1 | |
| x2x1x2 | 0,009 | 0 | 0 | 0 | 1 | 0 |
| x1x2x2 | 0,009 | 0 | 0 | 0 | 0 | 1 |
| x2x2x2 | 0,001 | 0 | 0 | 0 | 0 | 0 |
Среднее число символов на блок равно 1,59, а на знак - 0,53, что всего на 12% больше энтропии.
Следует подчеркнуть, что увеличение эффективности кодирования при укрупнении блоков не связано с учетом все более далеких статистических связей, т.к. нами рассматривались алфавиты с независимыми знаками.
Повышение эффективности определяется лишь тем, что набор вероятностей получившихся при укрупнении блоков можно делить на более близкие по суммарным вероятностям подгруппы.
Рассмотренная методика Шеннона - Фано не всегда приводит к однозначному построению кода, т.к. при разбиении на подгруппы можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы:
Таблица 3.6.
| Знаки (буквы) xi | Вероятность Pi | 1-е кодовые комбинации | 2-е кодовые комбинации | ||||||||
| номер разбиения | номер разбиения | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||
| x1 | 0,22 | 1 | 1 | 1 | 1 | ||||||
| x2 | 0,20 | 1 | 0 | 1 | 1 | 0 | |||||
| x3 | 0,16 | 1 | 0 | 0 | 0 | 1 | 1 | ||||
| x4 | 0,16 | 0 | 1 | 0 | 1 | 0 | |||||
| x5 | 0,10 | 0 | 0 | 1 | 0 | 0 | 1 | ||||
| x6 | 0,10 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| x7 | 0,04 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| x8 | 0,02 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
От указанного недостатка свободен метод Хаффмона.
Эта методика гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.
Для двоичного кода метод Хаффмона сводится к следующему. Буквы алфавита сообщений выписывают в основной столбец таблицы в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятности букв, не участвующих в объединении и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяются.
Процесс продолжается до тех пор, пока не получат единственную вспомогательную букву с вероятностью, равной единице.
Используя метод Хаффмона, осуществим эффективное кодирование ансамбля из восьми знаков:
Таблица 3.7.
| Знаки | Вероятности | Вспомогательные столбцы | Новая комбинация | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| x1 | 0,22 | 0,22 | 0,22 | 0,26 | 0,32 | 0,42 | 0,58 | 1 | 01 |
| x2 | 0,20 | 0,20 | 0,20 | 0,22 | 0,26 | 0,32 | 0,42 | 00 | |
| x3 | 0,16 | 0,16 | 0,16 | 0,20 | 0,22 | 0,26 | 111 | ||
| x4 | 0,16 | 0,16 | 0,16 | 0,16 | 0,20 | 110 | |||
| x5 | 0,10 | 0,10 | 0,10 | 0,16 | 100 | ||||
| x6 | 0,10 | 0,10 | 1011 | ||||||
| x7 | 0,04 | 0,06 | 10101 | ||||||
| x8 | 0,02 | 10100 | |||||||
Для наглядности построим кодовое дерево. Из точки, соответствующей вероятности 1, направляем две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей 0.
Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до вероятности каждой буквы.
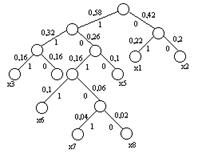
Рис. 3.1.
Двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.
Пример21: Используя метод Шеннона - Фано и метод Хаффмона осуществить эффективное кодирование алфавита русского языка, характеризующегося ансамблем, представленным в примере 4.
Похожие работы
... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается используемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...
... , 1968. - 340 с.]. В связи с этим логично было бы далее предположить, что она не предполагает строго количественного эквивалента, подобно энергии или материи. Но парадокс классической теории информации именно в том и состоит, что в её основе лежит предположение Р.Хартли, согласно которому информация допускает количественную оценку [Hartley R.V.L. Transmission of Information // BSTJ.- 1928. - V.7 - ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... с явлениями, которых, может быть, никогда не было и никогда не будет. Память каждого объекта всегда ограничена, а большая часть поступающей информации так и остается невостребованной. При этом общее ее количество (с точки зрения переносящих ее информационных кодов), безусловно, превышает возможности полного ее запоминания. Для предотвращения переполнения памяти и соответственно потери возможности ...
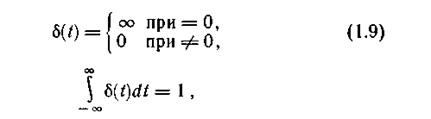
0 комментариев