Навигация
Условная энтропия
2.3 Условная энтропия
До сих пор предполагалось, что все элементы сообщения независимы, т.е. появление каждого данного элемента никак не связано с предшествующими элементами.
Рассмотрим теперь два ансамбля
Х = (х1, x2, ... ,xr)
Y = (y1, y2, ..., ys) ,
которые определяются не только собственными вероятностями р(хi) и p(yj), но и условными вероятностями pxi(yj), pyj(xi), где i = 1, 2, ... , r ; j = 1, 2, ... , s.
Систему двух случайных величин (сообщений) Х, Y можно изобразить случайной точкой на плоскости. Событие, состоящее в попадании случайной точки (X, Y) в область D, принято обозначать в виде (X, Y) Ì D.
Закон распределения системы двух случайных дискретных величин может быть задан с помощью табл. 2.5.
 Таблица 2.5.
Таблица 2.5.
| Y X | y1 | y2 | . . . | ys |
| x1 | Р11 | Р12 | . . . | Р1s |
| x2 | Р21 | Р22 | . . . | Р2s |
| : | : | : | : | : |
| xr | Рr1 | Рr2 | . . . | Рrs |
где Рij - вероятность события, заключающегося в одновременном выполнении равенства Х = xi, Y = yj. При этом
![]() .
.
Закон распределения системы случайных непрерывных величин (Х, Y) задают при помощи функции плотности вероятности р(x, y).
Вероятность попадания случайной точки (Х,Y) в область D определяется равенством
![]() .
.
Функция плотности вероятности обладает следующими свойствами:
1) р(x,y) ³ 0
2) ![]()
Если все случайные точки (X,Y) принадлежат области D, то
![]() .
.
Условным распределением составляющей Х при Y = yj (yj сохраняет одно и то же значение при всех возможных значениях Х) называют совокупность условных вероятностей Pyj(x1), Pyj(x2), ... , Pyj(xr)
Аналогично определяется условное распределение составляющей Y.
Условные вероятности составляющих X и Y вычисляют соответственно по формулам:
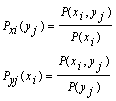
Для контроля вычислений целесообразно убедиться, что сумма вероятностей условного распределения равна единице.
Так как условная вероятность события yj при условии выполнения события xi принимается по определению
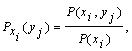
то вероятность совместного появления совокупности состояний
P(xi,yj) = P(xi) Pxi(yj).
Аналогично, условимся вероятность события xi при условии выполнения события yj:
![]() .
.
Поэтому общую энтропию зависимых ансамблей X и Y определяют по формуле Шеннона:
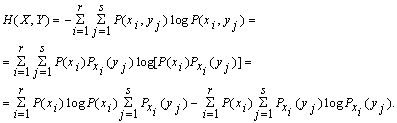
С учетом соотношения ![]() получают
получают
Н(Х,Y) = H(X) + HX(Y), где Н(Х) - энтропия ансамбля Х;
HX(Y) - условная энтропия ансамбля Y при условии, что сообщение ансамбля Х известны:
![]()
Для независимых событий Х и Y: Pxi(yj) = P(yj) и поэтому
HX(Y) = Н(Y) и, следовательно, Н(Х,Y) = H(X) + H(Y).
Если Х и Y полностью зависимы, т.е. при появлении xi неизбежно следует yj, то Р(xi,yj) равна единице при i = j и нулю при i ¹ j. Поэтому НX(Y) = 0, и , следовательно, Н(X,Y) = Н(Х), т.е. при полной зависимости двух ансамблей один из них не вносит никакой информации.
Полученное выражение для условной энтропии
![]()
можно использовать и как информативную характеристику одного ансамбля Х, элементы которого взаимно зависимы. Положив Y = X, получим
![]()
Например, алфавит состоит из двух элементов 0 и 1. Если эти элементы равновероятны, то количество информации, приходящееся на один элемент сообщения: Н0 = log m = log 2 = 1 бит. Если же, например, Р(0)=ѕ, а Р(1) = ј, то
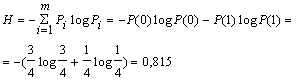
В случае же взаимной зависимости элементов, определяемой, например, условными вероятностями Р0(0) = 2/3; P0(1) = 1/3; P1(0) = 1; P1(1) = 0, то условная энтропия
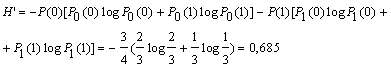
Энтропия при взаимно зависимых элементах всегда меньше, чем при независимых, т.е. H’<H.
Пример9: Задано распределение вероятностей случайной дискретной двумерной величины:
Таблица 2.6.
| Y X | 4 | 5 |
| 3 | 0,17 | 0,10 |
| 10 | 0,13 | 0,30 |
| 12 | 0,25 | 0,05 |
Найти законы распределения составляющих Х и Y.
Решение: 1) Сложив вероятности “по строкам”, получим вероятности возможных значений Х:
Р(3) = 0,17 + 0,10 = 0,27
P(10) = 0,13 +0,30 = 0,43
P(12) = 0,25 + 0,05 = 0,30.
Запишем закон распределения составляющей Х:
Таблица 2.7.
| Х | 3 | 10 | 12 |
| P(xi) | 0,27 | 0,43 | 0,30 |
Контроль: 0,27 + 0,43 + 0,30 = 1
2) Сложив вероятности “по столбцам”, аналогично найдем распределение составляющей Y:
Таблица 2.8.
| Y | 4 | 5 |
| P(yj) | 0,55 | 0,45 |
Контроль: 0,55 + 0,45 = 1
Пример10: Задана случайная дискретная двумерная величина (X,Y):
Таблица 2.9.
| Y X | y1 = 0,4 | y2 = 0,8 |
| x1 = 2 | 0,15 | 0,05 |
| x2 = 5 | 0,30 | 0,12 |
| x3 = 8 | 0,35 | 0,03 |
Найти: безусловные законы распределения составляющих; условный закон распределения составляющей Х при условии, что составляющая Y приняла значение y1 = 0,4; условный закон распределения составляющей Y при условии, что составляющая Х приняла значение х2 = 5
Решение: 1) Сложив вероятности “по строкам”, напишем закон распределения Х.
Таблица 2.10.
| X | 2 | 5 | 8 |
| P(x) | 0,20 | 0,42 | 0,38 |
2) Сложив вероятности “по столбцам”, найдем закон распределения Y.
Таблица 2.11.
| Y | 0,4 | 0,8 |
| P(y) | 0,80 | 0,20 |
3) Найдем условные вероятности возможных значений Х при условии, что составляющая Y приняла значение y1 = 0,4
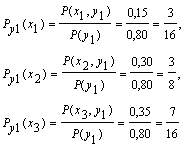
Напишем искомый условный закон распределения Х:
Таблица 2.12.
| X | 2 | 5 | 8 |
| Py1(xi) | 3/16 | 3/8 | 7/16 |
Контроль: 3/16 + 3/8 + 7/16 = 1
Аналогично найдем условный закон распределения Y:
Таблица 2.13.
| Y | 0,4 | 0,8 |
| Px2(yj) | 5/7 | 2/7 |
Контроль: 5/7 + 2/7 = 1.
Пример11: Закон распределения вероятностей системы, объединяющей зависимые источники информации X и Y, задан с помощью таблицы:
Таблица 2.14.
| Y X | y1 | y2 | y3 |
| x1 | 0,4 | 0,1 | 0 |
| x2 | 0 | 0,2 | 0,1 |
| x3 | 0 | 0 | 0,2 |
Определить энтропии Н(Х), H(Y), HX(Y), H(X,Y).
Решение: 1. Вычислим безусловные вероятности Р(xi) и Р(yj) системы:
а) сложив вероятности “по строкам” , получим вероятности возможных значений Х: P(x1) = 0,5
P(x2) = 0,3
P(x3) = 0,2
б) сложив вероятности “по столбцам”, получим вероятности возможных значений Y:
P(y1) = 0,4
P(y2) = 0,3
P(y3) = 0,3
2. Энтропия источника информации Х:
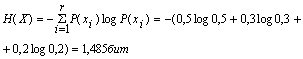
3. Энтропия источника информации Y:
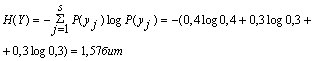
4. Условная энтропия источника информации Y при условии, что сообщения источника Х известны:
![]()
Так как условная вероятность события yj при условии выполнения события хi принимается по определению
![]()
поэтому найдем условные вероятности возможных значений Y при условии, что составляющая Х приняла значение x1:
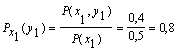
![]()
![]()
Для х2: ![]()
![]()
![]()
Для х3: 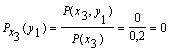
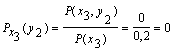
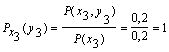
Поэтому: HX(Y) = - [0,5 (0,8 log 0,8 + 0,2 log 0,2) +
+0,3 (0,67 log 0,67 + 0,33 log 0,33) + 0,2 (1 log 1)] = 0,635
5. Аналогично, условная энтропия источника информации Х при условии, что сообщения источника Y известны:
![]()
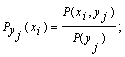
Для у1: ![]()
![]()
![]()
Для у2: ![]()
![]()
![]()
Для у3: ![]()
![]()
![]()
![]()
6. Общая энтропия зависимых источников информации Х и Y:
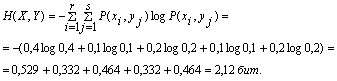
Проверим результат по формуле:
Н(Х,Y) = H(X) +HX(Y) = 1,485 + 0,635 = 2,12 бит
Н(Х,Y) = H(Y) +HY(X) = 1,57 + 0,55 = 2,12 бит
Пример12: Известны энтропии двух зависимых источников Н(Х) = 5бит; Н(Y) = 10бит. Определить, в каких пределах будет изменяться условная энтропия НХ(Y) в максимально возможных пределах.
Решение: Уяснению соотношений между рассматриваемыми энтропиями источников информации способствует их графическое отображение.
При отсутствии взаимосвязи между источниками информации:
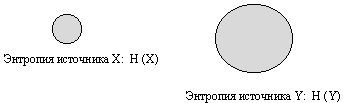
Рис. 2.5.
Если источники информации независимы, то НХ(Y) = Н(Y) = 10 бит, а НY(X) = H(X) = 5 бит, и, следовательно, Н(X,Y) = H(X) + H(Y) = 5 +10 = 15 бит. Т.е., когда источники независимы НХ(Y) = Н(Y) = 10 бит и поэтому принимают максимальное значение.
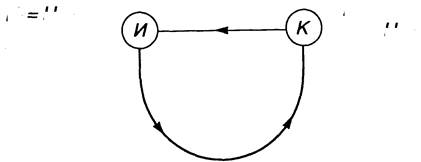
По мере увеличения взаимосвязи источников НХ(Y) и НY(X) будут уменьшаться:
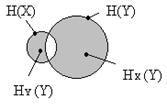
Рис. 2.6.
При полной зависимости двух источников один из них не вносит никакой информации, т.к. при появлении xi неизбежно следует уj , т.е. Р(xi, уj) равно единице при i = j и нулю при i ¹ j. Поэтому
НY(X) = 0 и, следовательно, Н(X,Y) = НХ(Y) .
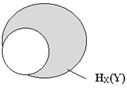
Рис. 2.7.
При этом НХ(Y) = Н(Y) - Н(Х) = 10 - 5 = 5 бит. Поэтому НХ(Y) будет изменяться от 10 бит до 5 бит при максимально возможном изменении Нy(Х) от 5 бит до 0 бит.
Пример13: Определите Н(Х) и НХ(Y), если Р(х1,y1) = 0,3; P(x1,y2) = 0,2;
P(x3,y2) = 0,25; P(x3,y3) = 0,1
Пример14: Определите Н(Х), H(Y), H(X,Y), если Р(х1,y1) = 0,2; P(x2,y1) = 0,4;
P(x2,y2) = 0,25; P(x2,y3) = 0,15
Похожие работы
... порядок чередования букв формируется согласно правилам, заданным верхними иерархическими уровнями текста, то есть не «снизу вверх», а «сверху вниз». Что же касается используемой теорией информации вероятностной функции энтропии, то она может быть использована в качестве точного математического инструмента только на нижних уровнях иерархии текста, поскольку только на этих уровнях удается найти ...
... , 1968. - 340 с.]. В связи с этим логично было бы далее предположить, что она не предполагает строго количественного эквивалента, подобно энергии или материи. Но парадокс классической теории информации именно в том и состоит, что в её основе лежит предположение Р.Хартли, согласно которому информация допускает количественную оценку [Hartley R.V.L. Transmission of Information // BSTJ.- 1928. - V.7 - ...
... связано с приложением теории в технике связи - рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации. Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В ...
... с явлениями, которых, может быть, никогда не было и никогда не будет. Память каждого объекта всегда ограничена, а большая часть поступающей информации так и остается невостребованной. При этом общее ее количество (с точки зрения переносящих ее информационных кодов), безусловно, превышает возможности полного ее запоминания. Для предотвращения переполнения памяти и соответственно потери возможности ...
0 комментариев