Навигация
Основные типы локальных регуляторов
3.2.2 Основные типы локальных регуляторов
Множество локальных регуляторов можно упорядочить по различным признакам:
Во-первых, в зависимости от характера информации, используемой в регуляторе:
1.) С регулированием по разомкнутому циклу (по возмущениям).
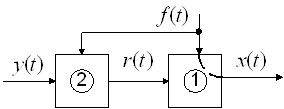
Проблема состояла в определении регулирующего воздействия.
Здесь регулятор настраивается в зависимости от основного возмущения ![]() .
.
“+”: высокое быстродействие, так как регулятор настраивается сразу по возмущению, а не так, как в случае регулирования по замкнутому циклу.
“–”: трудность программирования регулятора на возможные возмущения, следовательно, невысокая точность.
2.) С регулированием по замкнутому циклу (по отклонениям).
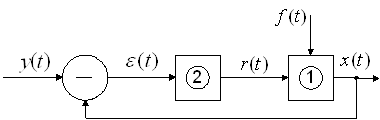
“+”: в независимости от причин появления ошибки ![]() , система работает по принципу её (ошибки) компенсации.
, система работает по принципу её (ошибки) компенсации.
“–”: быстродействие ниже, чем в случае с регулированием по разомкнутому циклу.
3.) С регулированием по комбинированию.
Объединение случаев регулирования по разомкнутому циклу и по замкнутому циклу.
Во-вторых, в зависимости от уставки ![]() :
:
1.) Системы стабилизации ![]() .
.
2.) Программные системы ![]() , причём
, причём ![]() — известно.
— известно.
3.) Следящие системы ![]() , причём
, причём ![]() — заранее неизвестная функция.
— заранее неизвестная функция.
В-третьих, в зависимости от размерности n вектора состояния ![]() :
:
1.) Одномерные n = 1.
2.) Двумерные n = 2.
3.) Многомерные n = 3.
В-четвёртых, в зависимости от количества контуров в системе:
1.) Одноконтурные (используется только главная обратная связь, нет местных связей).
2.) Двухконтурные (используются одна главная и одна местная обратные связи).
3.) Многоконтурные (используются одна главная и много местных обратных связей).
В-пятых, в зависимости от установившегося значения ошибки:
1.) Статические ![]() .
.
2.) Астатические ![]() .
.
Систему называют астатической по управляющему (или возмущающему) воздействию, если при подаче на вход постоянного управляющего (или возмущающего) воздействия ошибка в установившемся состоянии не зависит от величины этого воздействия и равна нулю.
Сравнить рисунки 24 и 26 методических указаний.
В-шестых, в зависимости от характеров сигналов, циркулирующих в системе:
1.) Непрерывные.
2.) Импульсные.
3.) Релейные.
4.) Релейно-импульсные (кодово-импульсные).
5.) На переменном токе (с гармонической модуляцией).
1.) В непрерывных системах сигналы могут быть описаны непрерывными во времени функциями.
3.2.2.1 Импульсные системы
Эти системы содержат импульсные устройства (2), осуществляющие квантование сигналов по времени (АИМ).
Типовая структура импульсных систем:

1 — непрерывная часть системы.
Импульсное устройство (ключ), замыкаясь в дискретные равноотстоящие моменты времени (t = i∙T, i = 0, 1, 2, …, где i — период повторения, а T — период дискретности), преобразует непрерывный входной сигнал ![]() в дискретный
в дискретный ![]() .
.
Реальный ключ (2) удобно условно представить в следующем виде:

3 — идеальный ключ; 4 — формирователь.
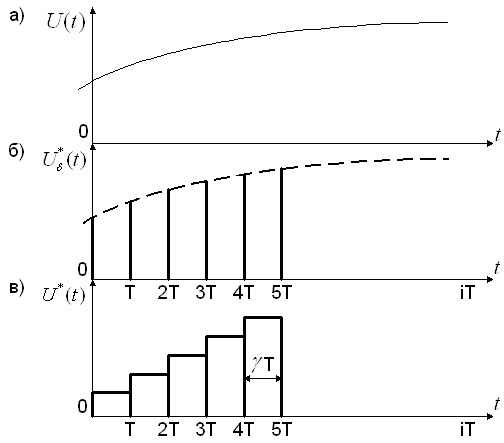
Лекция №4. 19.02.2003
Идеальный ключ (3) преобразует непрерывный сигнал ![]() (рисунок а)) в последовательность идеальных импульсов типа δ-функций (рисунок б)), далее эта последовательность поступает на формирователь (4).
(рисунок а)) в последовательность идеальных импульсов типа δ-функций (рисунок б)), далее эта последовательность поступает на формирователь (4).
Формирователь (4) преобразует эту последовательность в реальные импульсы определённой формы, длительности (γT, 0<γ≤1) и амплитуды (рисунок в)).
При запоминании на интервале дискретности T при γ = 1 формирователь (4) называют Экстраполятором Нулевого Порядка (Э0П).
Математическая модель Э0П непрерывна и может быть отнесена к непрерывной части системы. В результате типовая структура импульсной системы примет вид:
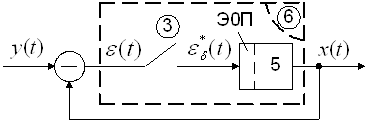
Рисунок № !
5 — приведенная непрерывная часть;
6 — импульсный фильтр
3.2.2.2 Релейные системы
Релейные системы содержат в своей структуре устройства (реле), осуществляющие квантование сигнала по уровню. В результате, на выходе реле сигнал будет непрерывным, но ступенчатым
3.2.2.3 Релейно-импульсные системы
В них происходит квантование сигналов по времени и по уровню.
К этому типу относятся цифровые системы управления, в частности АСУТП с используемым ВК.
При большом количестве разрядов АЦП и ЦАП квантованием можно пренебречь, и отнести такие системы к импульсным.
Похожие работы
... существует внутренний механизм целеполагания. Наука, которая первой начала исследование подобных систем, получила название кибернетики. Кибернетика Кибернетика (от греч. kybernetike - искусство управления) — это наука об управлении сложными системами с обратной связью. Она возникла на стыке математики, техники и нейрофизиологии, и ее интересовал целый класс систем, как живых, так и неживых, ...
... действие внутренних тенденций, и система сама построит необходимую структуру. Нужно только знать потенциальные возможности данной среды и способы их стимуляции. В основе синергетического подхода к управлению социальными системами – механизм резонансных направляющих воздействий на нелинейную систему, в ходе развития которой всегда существует область параметров и стадий, в рамках которых нелинейная ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... , учитывая, что окружение будет меняться. Смысл стратегического управления в определении и осуществлении действий предприятия в настоящее время для обеспечения достойного будущего, а не разработка действий, которые будет осуществлять организация в дальнейшем. 1.2 Особенности стратегического подхода к управлению Стратегический подход к управлению не является идеальным решением дальнейшего ...

0 комментариев