Основные типы локальных регуляторов
Системы на переменном токе
Управляемость систем
Разностные уравнения
Преобразование Лапласа непрерывных функций
Математические модели систем управления в пространстве состояний
Интегрирующее звено
Дифференцирующее звено второго порядка
Неустойчивое периодическое звено
Неминимально-фазовое дифференцирующее звено первого порядка
Звено чистого запаздывания
Решение уравнения состояния
Передаточная функция
Переходная функция
Дискретная передаточная функция импульсной системы с экстраполятором нулевого порядка
Частотные характеристики
Дискретные системы
Дискретные системы
Навигация
Управляемость систем
Управление сложными системами
55819
знаков
37
таблиц
113
изображений
3.3.4 Управляемость систем
Понятие управляемости означает, можно ли, вообще, управлять системой. Иногда это можно установить по структуре системы:
Пример № 1.
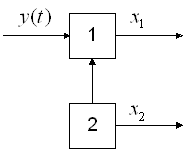
Система неуправляема, так как управление 
не управляет второй подсистемой.
3.3.5 Наблюдаемость
С качественной точки зрения под наблюдаемостью системы понимают способность состояния системы создавать выходной сигнал.
Пример № 2.
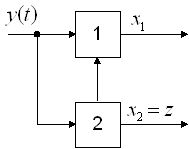
Система не наблюдаема, так как измеряется 
, а 
не измеряется.
Пример № 3.
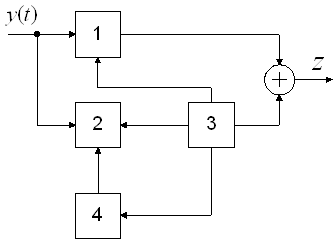
1 подсистема — управляема и наблюдаема.
2 подсистема — управляема и не наблюдаема.
3 подсистема — не управляема и наблюдаема.
4 подсистема — не управляема и не наблюдаема.
Лекция №5. 25.02.2003
Раздел 4. Математические модели систем управления
4.1. Основные виды математических моделей
Математические модели могут быть:
1.) Линейными;
2.) Нелинейными
В свою очередь каждая из них может быть:
1.) Непрерывной (система дифференциальных или интегро-дифференциальных уравнений);
2.) Дискретной (система разностных уравнений);
3.) Дискретно-непрерывной (сочетание непрерывной и дискретной систем).
В свою очередь каждая из них может быть:
1.) Стационарной;
2.) Нестационарной.
Математическая модель нестационарна, если хотя бы один из параметров системы изменяется с течением времени.
В свою очередь каждая из них может быть:
1.) С сосредоточенными параметрами;
2.) С сосредоточенными и распределёнными параметрами.
1.) Физические параметры системы (например, масса, скорость, потенциал и др.) обычно сосредоточены в точке (так можно считать), коэффициенты дифференциальных уравнений зависят от этих параметров. В результате, математическая модель будет, например, системой дифференциальных уравнений в полных производных (
).
2.) Если система содержит одну из подсистем (например, канал связи, трубопровод), параметры которой распределены в пространстве, то математическая модель такой системы будет содержать, например, систему дифференциальных уравнений в частных производных (
).
В свою очередь каждая из них может быть:
1.) Детерминированной;
2.) Стохастической или со случайными параметрами (если хотя бы один из параметров или воздействий является случайной функцией или величиной).
и др.
4.1.1 Математические модели в области вещественной переменной (временной области)
4.1.1.1 Дискретные математические модели
4.1.1.1.1 Решетчатые функции
Решетчатая функция (РФ) — функция, существующая в дискретны равноотстоящие друг от друга значения независимой переменной и равная нулю между этими значениями аргумента.
Пример такой функции:
смотри рисунок б) лекции №3.
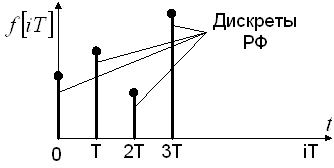
— РФ, 
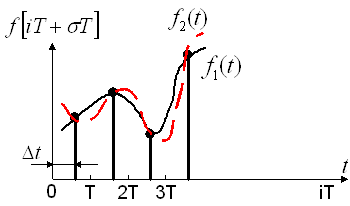
Функции f(t) соответствует функция , 
(
)
Одной и той же РФ соответствует множество огибающих непрерывных функций (смотри рисунок выше):
— огибающие функции.
Если ввести безразмерное время 
, то 
будет соответствовать РФ 
. 
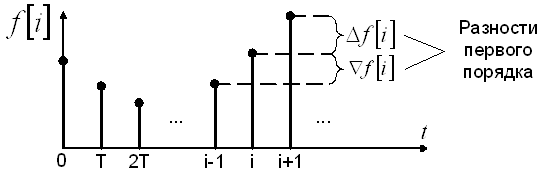
Решетчатую функцию характеризуют её разности и суммы
Разность может быть прямой (
) и обратной (
).
.
Аналогом интеграла непрерывной функции для РФ являются её суммы:
1) Полная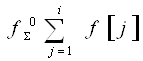 
;
2) Неполная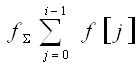
.
Похожие работы
... существует внутренний механизм целеполагания. Наука, которая первой начала исследование подобных систем, получила название кибернетики. Кибернетика Кибернетика (от греч. kybernetike - искусство управления) — это наука об управлении сложными системами с обратной связью. Она возникла на стыке математики, техники и нейрофизиологии, и ее интересовал целый класс систем, как живых, так и неживых, ...
... действие внутренних тенденций, и система сама построит необходимую структуру. Нужно только знать потенциальные возможности данной среды и способы их стимуляции. В основе синергетического подхода к управлению социальными системами – механизм резонансных направляющих воздействий на нелинейную систему, в ходе развития которой всегда существует область параметров и стадий, в рамках которых нелинейная ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... , учитывая, что окружение будет меняться. Смысл стратегического управления в определении и осуществлении действий предприятия в настоящее время для обеспечения достойного будущего, а не разработка действий, которые будет осуществлять организация в дальнейшем. 1.2 Особенности стратегического подхода к управлению Стратегический подход к управлению не является идеальным решением дальнейшего ...
0 комментариев