Навигация
Дискретная передаточная функция импульсной системы с экстраполятором нулевого порядка
5.4.2 Дискретная передаточная функция импульсной системы с экстраполятором нулевого порядка
Структура системы приведена на Рисунке № !.
Можно показать, что ДПФ такой системы в разомкнутом состоянии (когда убираем главную обратную связь) определяется по следующей формуле:
 !!!!
!!!!
W(s) — передаточная функция непрерывной части системы.
Пример № 2.
Определить ДПФ микропроцессорной (импульсной) системы (Рисунок № !), непрерывная часть которой следующая:
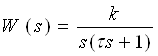
Решение:
1) 
2)  — раскладываем на простые дроби.
— раскладываем на простые дроби.
3) 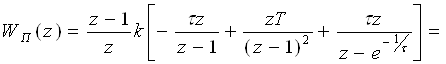

5.4.3 Дискретная передаточная функция многомерной системы
Задачу определения ДПФ для многомерного случая удобно решать Методом Пространств Состояний:
Рассмотрим алгоритм решения этой задачи для простейшего одномерного случая:
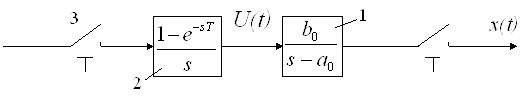
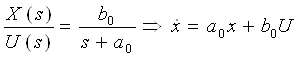 (смотри связь между ПФ и дифференциальным уравнением)
(смотри связь между ПФ и дифференциальным уравнением)
Известно, что решение этого дифференциального уравнения первого порядка: x(t0)=x0
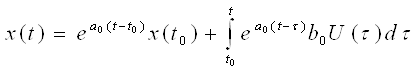
При U(t)=U[iT], iT ≤ t < (i+1)T интегрируя в пределах (iT, t):

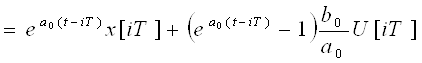 .
.
t=(i+1)T
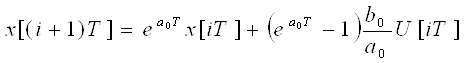 .
.
Применяя к этому выражению Z-преобразование с начальными нулевыми условиями, с учётом теоремы сдвига и свойств линейности:
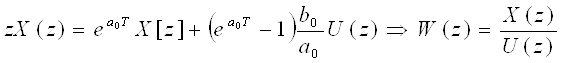
ММ многомерной системы приведена выше (смотри систему уравнений (III)). Применяя к этой системе Z-преобразование с нулевыми начальными условиями, с учётом свойств линейности получим:
 (III*)
(III*)
Эта ММ позволяет определить матричную дискретную передаточную функцию ![]() , элементы которой рассчитываются по следующим формулам:
, элементы которой рассчитываются по следующим формулам:
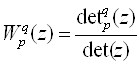 (1)
(1)
Здесь 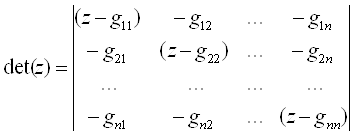 (2)
(2)
Определитель ![]() можно получить из определителя (2) путём замены q-столбца следующим столбцом:
можно получить из определителя (2) путём замены q-столбца следующим столбцом: ![]()
5.4.3.1 Пример № 3
По системе линейных разностных уравнений, полученных в примере (III′), определить дискретные передаточные функции от управления y к координатам x1 и x2.
![]()
![]()
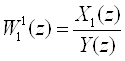
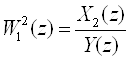
Лекция №11. 18.03.2003
Решение:
1) 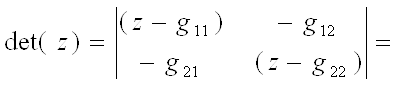
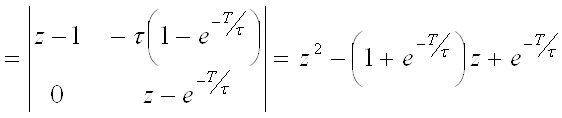 2)
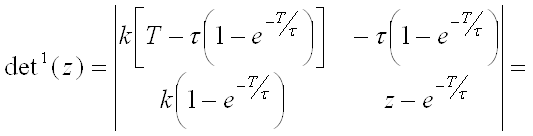
2) 
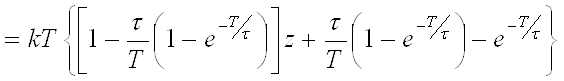
3) 
4) 
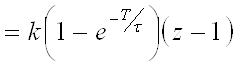
5) 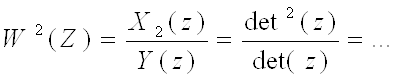
5.4.3.2 Численный расчёт дискретных передаточных функций многомерных систем
Если известно уравнение состояния ![]() то можно получить уравнение состояния многомерной импульсной системы
то можно получить уравнение состояния многомерной импульсной системы ![]() . При этом матрицы G, H΄, H определяются численно в виде рядов с использованием матриц А и В по приведённым выше формулам.
. При этом матрицы G, H΄, H определяются численно в виде рядов с использованием матриц А и В по приведённым выше формулам.
Реализация алгоритмов определения элементов ![]() требует операции раскрытия определителей (смотри Пример № 3). Эту задачу можно решить или классически (по известным методам), или численно. При высоком порядке системы более эффективны численные методы Фадеева, Крылова, Леверрье.
требует операции раскрытия определителей (смотри Пример № 3). Эту задачу можно решить или классически (по известным методам), или численно. При высоком порядке системы более эффективны численные методы Фадеева, Крылова, Леверрье.
Рассмотрим метод Фадеева:
Во-первых, определитель системы det(z) (2) является характеристическим многочленом матрицы G, следовательно:
![]()
Необходимо найти коэффициенты этого полинома: ![]() .
.
Алгоритм расчёта коэффициентов по Фадееву:
| 1 этап: 1 шаг: 2 шаг: 3 шаг:
| 2 этап: 1 шаг: 2 шаг: 3 шаг:
|
| Предпоследний этап: 1 шаг: 2 шаг: 3 шаг: | Последний этап: 1 шаг: 2 шаг: 3 шаг: |
Пример № 4.
Рассмотрим систему второго порядка: 
Поиск методом Фадеева:
1) 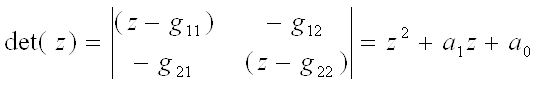 , в котором неизвестны a1 и a0.
, в котором неизвестны a1 и a0.
2) а)  б)
б) ![]()
в) 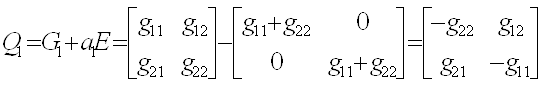
3) а) 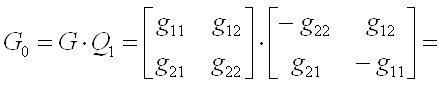
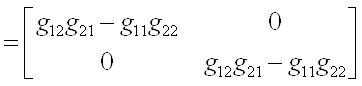 б)
б) 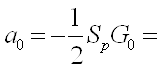
![]() в) Контроль:
в) Контроль: ![]()
Во-вторых, ![]() отличен от определителя системы (III*)
отличен от определителя системы (III*)
Для расчёта коэффициента этого определителя можно использовать найденные значения коэффициентов ai.
Пусть 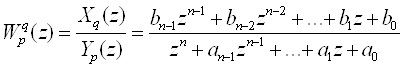 (3)
(3)
![]()
![]() (4)
(4)
Если подать на вход исходной системы (III*) какой-либо известный входной сигнал yp[iT], i = 0, 1, 2, … при нулевых остальных входных сигналах y1[iT]= y2[iT]=…= yp-1[iT]= yp+1[iT]=…=0 и при нулевых начальных условиях x1[0]=x2[0]=…=0, то путём непосредственных расчётов по системе (III*) (смотри задачу семинара №2) можно последовательно получить значения x[T], x[2T], …, x[iT].
Если подать тот же самых сигнал Yp на вход разностного уравнения (4) при нулевых начальных условиях (x[0]=x[–T]=…=0), то дискреты xq[iT] уравнения (4) совпадут с сигналами xq[iT] вектора X[iT], расcчитанного по уравнению (III*).
Тогда можно показать, что:
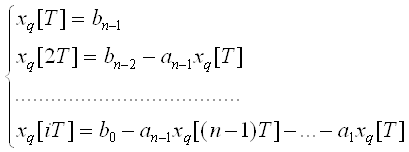
при входном сигнале 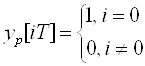 (*)
(*)
 (5)
(5)
Пример № 5.
Рассмотрим систему второго порядка, своего рода (III*) при n=2.
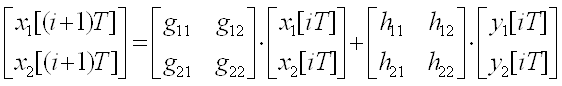
Для системы второго порядка определить дискретную передаточную функцию 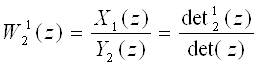 при нулевых начальных условиях.
при нулевых начальных условиях.
Решение:
1) det(z) определён в примере № 4.
2) Составляем разностное уравнение p=2, n=2, q=1:

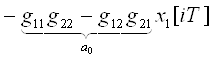 (4΄)
(4΄)
3) Рассчитываем переходный процесс по исходной системе (III*) при n=2:
i=0

(смотри условие (*)).
![]()
i=1

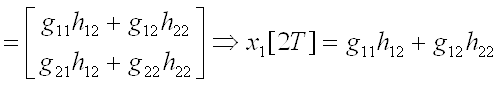
4) Определяем коэффициенты:
![]()
![]()
![]() .
.
Лекция №12. 25.03.2003
Похожие работы
... существует внутренний механизм целеполагания. Наука, которая первой начала исследование подобных систем, получила название кибернетики. Кибернетика Кибернетика (от греч. kybernetike - искусство управления) — это наука об управлении сложными системами с обратной связью. Она возникла на стыке математики, техники и нейрофизиологии, и ее интересовал целый класс систем, как живых, так и неживых, ...
... действие внутренних тенденций, и система сама построит необходимую структуру. Нужно только знать потенциальные возможности данной среды и способы их стимуляции. В основе синергетического подхода к управлению социальными системами – механизм резонансных направляющих воздействий на нелинейную систему, в ходе развития которой всегда существует область параметров и стадий, в рамках которых нелинейная ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... , учитывая, что окружение будет меняться. Смысл стратегического управления в определении и осуществлении действий предприятия в настоящее время для обеспечения достойного будущего, а не разработка действий, которые будет осуществлять организация в дальнейшем. 1.2 Особенности стратегического подхода к управлению Стратегический подход к управлению не является идеальным решением дальнейшего ...



0 комментариев