Основные типы локальных регуляторов
Системы на переменном токе
Управляемость систем
Разностные уравнения
Преобразование Лапласа непрерывных функций
Математические модели систем управления в пространстве состояний
Интегрирующее звено
Дифференцирующее звено второго порядка
Неустойчивое периодическое звено
Неминимально-фазовое дифференцирующее звено первого порядка
Звено чистого запаздывания
Решение уравнения состояния
Передаточная функция
Переходная функция
Дискретная передаточная функция импульсной системы с экстраполятором нулевого порядка
Частотные характеристики
Дискретные системы
Дискретные системы
Навигация
Преобразование Лапласа непрерывных функций
Управление сложными системами
55819
знаков
37
таблиц
113
изображений
4.1.2.2 Преобразование Лапласа непрерывных функций
Рассмотрим f1(t)=f(t)e-ct, c=const такая, что:
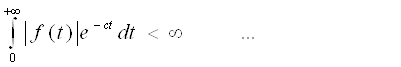(4)
При этом для существования этого интеграла от функции f(t) пришлось потребовать выполнения условия f(t)=0 
t<0.
c>c0 (c0 — абсцисса абсолютной сходимости).
Для [1(t)] с0=0
Для e-αtс0=α
Для eαtс0=-α
Для sinαt с0=0
Тогда получим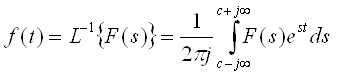 
(5)
Это интеграл Лапласа или формула обращения в преобразовании Лапласа.
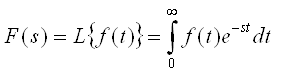(6)
f(t)
F(s)
4.1.2.3 Нули и полюсы изображения F(s)
F(s) — дробно рациональная функция. 
Корни полиномов R(s) и Q(s) определяют свойства изображения или свойства этой функции.
4.1.2.3.1 Нули изображения F(s)
Представим F(s) в следующем виде:
, а 
, значит F(s) имеет ноль кратности m в точке 
.
4.1.2.3.2 Полюса изображения F(s)
Полюса изображения F(s) — это корни полинома знаменателя Q(s).
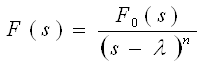, где 
,
а 
, т.е. изображение F(s) содержит полюс кратности n при 
.
На комплексной плоскости s нули обозначают “0”, а полюса “Х”.
4.1.2.4 Дискретное преобразование Лапласа
Данное преобразование применяется для решетчатых функций.
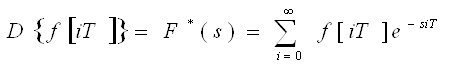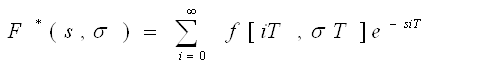(7)
(7΄)
4.1.2.5 Z-преобразование
Введём новую комплексную переменную z=est, тогда (7) можно представить в следующем виде:
≜ 
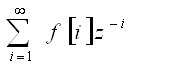(8)!!!!
s=c+j∞
Выбрав c>c0 ряд (8) будет сходиться, и решетчатой функции будет соответствовать Z-преобразование. f[i]F(z).
Z-преобразование применяют и к непрерывным функциям. При этом, если для РФ f[i] прямая и обратная задачи однозначны, то для непрерывной функции задача определения оригинала f[i] по его изображению не однозначна.
4.1.2.6 Основные свойства преобразования Лапласа и Z-преобразования
| Свойства преобразования Лапласа | Свойства Z-преобразования |
| 1. Свойство линейности:
| 1. Свойство линейности:
|
| 2. Теорема о конечном значении: Если функция s∙F(s) является аналитической в правой полуплоскости и на мнимой оси, то
| 2. Теорема о конечном значении:
|
| 3. Теорема о начальном значении: Если | 3. Теорема о начальном значении:
|
| 4. Теорема сдвига в области вещественной переменной:
t-τ — запаздывание (по оси вправо). t+τ — упреждение (по оси влево). | 4. Теорема сдвига в области вещественной переменной:
|
| 5. Свойство дифференцирования: Если начальные условия нулевые, то | |
| 6. Свойство интегрирования: при нулевых начальных условиях
| |
| 7. Теорема свёртки:
|
, то 
, где k — целое число, кратное периоду дискретности.
Лекция №7. 04.03.2003
8. Задача определения оригинала функции по её изображению:
а) Непрерывные функции
Смотри формулу (5) из пункта № 4.1.2.2.
б) Дискретные математические модели (для решетчатых функций)
Так как F(z) дробно рациональная функция, то проще эту задачу решать так: разделив числитель на знаменатель, F(z) можно разложить в ряд Лорана по убывающим степеням, т.е.
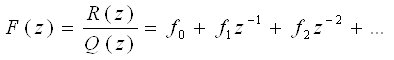
Известно, что 
≜
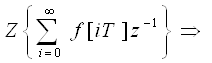
f0, f1, f2, … — дискреты искомой решетчатой функции f[iT].
4.1.2.7 Математические модели в комплексной области
4.1.2.7.1 Дискретные математические модели
Применяя к уравнению (Ⅰ) пункта № 4.1.1.1.2 Z-преобразование, с учётом свойств линейности и теоремы сдвига при нулевых начальных условиях получим:
(I*)
4.1.2.7.2 Непрерывные математические модели
Применяя к уравнению (Ⅱ) пункта № 4.1.1.2.2 преобразование Лапласа при нулевых начальных условиях, с учётом свойств линейности и дифференцирования получим:
(II*)
Похожие работы
... существует внутренний механизм целеполагания. Наука, которая первой начала исследование подобных систем, получила название кибернетики. Кибернетика Кибернетика (от греч. kybernetike - искусство управления) — это наука об управлении сложными системами с обратной связью. Она возникла на стыке математики, техники и нейрофизиологии, и ее интересовал целый класс систем, как живых, так и неживых, ...
... действие внутренних тенденций, и система сама построит необходимую структуру. Нужно только знать потенциальные возможности данной среды и способы их стимуляции. В основе синергетического подхода к управлению социальными системами – механизм резонансных направляющих воздействий на нелинейную систему, в ходе развития которой всегда существует область параметров и стадий, в рамках которых нелинейная ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... , учитывая, что окружение будет меняться. Смысл стратегического управления в определении и осуществлении действий предприятия в настоящее время для обеспечения достойного будущего, а не разработка действий, которые будет осуществлять организация в дальнейшем. 1.2 Особенности стратегического подхода к управлению Стратегический подход к управлению не является идеальным решением дальнейшего ...
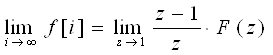
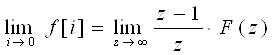
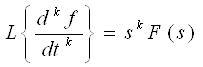
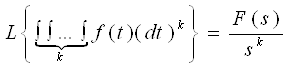
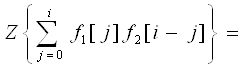
0 комментариев