Навигация
Частотные характеристики
5.5 Частотные характеристики
5.5.1 Непрерывные системы
Рассмотрим ММ стационарной непрерывной системы:
![]() (1)
(1)
Пусть ![]()
![]()
На основе формулы Эйлера (![]() ):
):
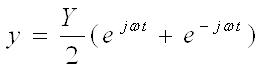 , начальные условия нулевые.
, начальные условия нулевые.
При нулевых начальных условиях решение уравнения (1) можно получить в виде двух слагаемых x(t)=x1(t)+x2(t).
При этом с учётом принципа суперпозиции: x1(t)![]() y1(t), x2(t)
y1(t), x2(t)![]() y2(t).
y2(t).
Найдём x1(t):
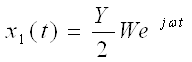 , где W — пока неизвестная и не зависящая от времени функция.
, где W — пока неизвестная и не зависящая от времени функция.
Подставляя в уравнение (1) x1, y1 и их соответствующие производные, получим:
![]()
![]()
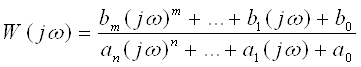 … (2)
… (2)
![]() Комплексно-частотную характеристику системы
Комплексно-частотную характеристику системы ![]() можно получить передаточной функции путём замены переменной
можно получить передаточной функции путём замены переменной ![]() (смотри уравнение (1) раздела 5.1.1.).
(смотри уравнение (1) раздела 5.1.1.).
Комментарий:
![]() , … (3)
, … (3)
|
|
|
|
Здесь: ![]()
![]()
![]()
![]()
Смотри методические указания, страница 18.
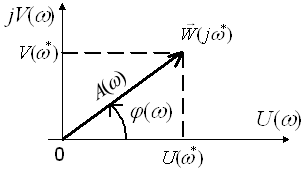
![]() , … (4)
, … (4)
где ![]() — Амплитудно-частотная характеристика (АЧХ).
— Амплитудно-частотная характеристика (АЧХ).
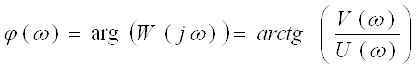 — Фазово-частотная характеристика (ФЧХ).
— Фазово-частотная характеристика (ФЧХ).
Пример смотри в методических указаниях, рисунки 11 и 12.
При изменении ![]() конец вектора
конец вектора ![]() описывает кривую, называемую АФХ — амплитудно-фазовая характеристика или Катографом Найквиста (Рисунок 21 методических указаний).
описывает кривую, называемую АФХ — амплитудно-фазовая характеристика или Катографом Найквиста (Рисунок 21 методических указаний).
Физический смысл частотной характеристики: частотная характеристика — результат анализа вынужденного движения линейной стационарной системы при гармоническом воздействии.
Таким образом, 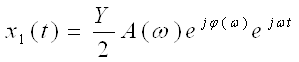 .
.
Аналогично можно определить составляющую
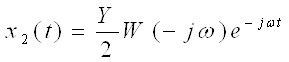 воздействия y2(t).
воздействия y2(t).
То есть 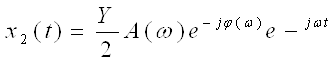 .
.
![]() … (5)
… (5)
Таким образом, если на входе рассматриваемой системы действует гармонический входной сигнал, то выходной сигнал будет также гармоническим (Формула (5)) и отличающимся от входного по амплитуде в ![]() раз, а по фазе на
раз, а по фазе на ![]() . Здесь
. Здесь ![]() — АЧХ, а
— АЧХ, а ![]() — ФЧХ.
— ФЧХ.
Замечание № 1:
Так как АФХ симметрична относительно вещественной оси ![]() для положительных и отрицательных значений
для положительных и отрицательных значений ![]() , то обычно ограничивают диапазон изменения
, то обычно ограничивают диапазон изменения ![]() :
: ![]() .
.
Замечание № 2:
Иногда вместо обычной АФХ ![]() рассматривают нормированную АФХ
рассматривают нормированную АФХ ![]() такую, что
такую, что ![]() , где
, где ![]() , а
, а ![]() — порядок астатизма системы, или обратную АФХ
— порядок астатизма системы, или обратную АФХ  , или обратно нормированную АФХ
, или обратно нормированную АФХ ![]() .
.
Замечание № 3:
Очень часто вместо АФХ ![]() используют Логарифмическую Частотную Характеристику (ЛЧХ).
используют Логарифмическую Частотную Характеристику (ЛЧХ).
а) ![]() — ЛАЧХ.
— ЛАЧХ.
б) 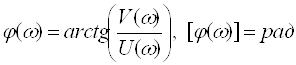 — ЛФЧХ.
— ЛФЧХ.
По оси абсцисс соответственно отмеряются либо ![]() , либо
, либо ![]() .
.
Примеры в методических указаниях — рисунки 12, 22, 25 а)
Примеры нормированных ЛЧХ ![]() — рисунки 23 и 25 б).
— рисунки 23 и 25 б).
Похожие работы
... существует внутренний механизм целеполагания. Наука, которая первой начала исследование подобных систем, получила название кибернетики. Кибернетика Кибернетика (от греч. kybernetike - искусство управления) — это наука об управлении сложными системами с обратной связью. Она возникла на стыке математики, техники и нейрофизиологии, и ее интересовал целый класс систем, как живых, так и неживых, ...
... действие внутренних тенденций, и система сама построит необходимую структуру. Нужно только знать потенциальные возможности данной среды и способы их стимуляции. В основе синергетического подхода к управлению социальными системами – механизм резонансных направляющих воздействий на нелинейную систему, в ходе развития которой всегда существует область параметров и стадий, в рамках которых нелинейная ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... , учитывая, что окружение будет меняться. Смысл стратегического управления в определении и осуществлении действий предприятия в настоящее время для обеспечения достойного будущего, а не разработка действий, которые будет осуществлять организация в дальнейшем. 1.2 Особенности стратегического подхода к управлению Стратегический подход к управлению не является идеальным решением дальнейшего ...
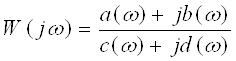

0 комментариев