Этапы развития тригонометрии как науки
Содержание и анализ материала по тригонометрии в различных школьных учебниках
Роль и место тригонометрических уравнений и неравенств в ШКМ
Однородные уравнения
Тригонометрические неравенства и методы их решения
Метод интервалов
Основные умения, необходимые при решении тригонометрических уравнений и неравенств
Группу составляют тригонометрические уравнения, способ решения которых основан на определениях и некоторых свойствах тригонометрических функций
Решение неравенства с помощью круга
Учащиеся не уделяют должного внимания определению области применимости некоторых формул и правил;
Сравнение результатов тестирования до и после эксперимента позволяет представить их в графической форме
Навигация
Этапы развития тригонометрии как науки
Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа
89437
знаков
1
таблица
28
изображений
1.1 Этапы развития тригонометрии как науки
Тригонометрия является одним из наиболее молодых отделов элементарной математики, получивших окончательное оформление лишь в XVIII в., хотя отдельные идеи её относятся к глубокой древности, к античному миру и к математическому творчеству индусов (К. Птолемей, II в., Аль Баттани, IX в., и др.). Европейские математики достигли высокой степени совершенства в вычислении таблиц натуральных синусов и тангенсов (Региомонтанус, XV в., Ретикус и Питискус, XVI в., и др.).
Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: 
(тригонон) – треугольник, 
(метрейн) – измерение.
Научная разработка тригонометрии осуществлена Л. Эйлером в его труде «Jntroductio in analysis infinitorum» (1748). Он создал тригонометрию как науку о функциях, дал ей аналитическое изложение, вывел всю совокупность формул из немногих основных формул. Обозначение сторон малыми буквами и противолежащих углов — соответствующими большими буквами позволило ему упростить все формулы, внести в них ясность и стройность. Эйлеру принадлежит мысль рассматривать тригонометрические функции как отношения соответствующих линий к радиусу круга, т. е. как числа, причём радиус круга как «полный синус» он принял за единицу. Эйлер получил ряд новых соотношений, установил связь тригонометрических функций с показательными, дал правило знаков функций для всех четвертей, получил обобщённую формулу приведения и освободил тригонометрию от многих ошибок, которые допускались почти во всех европейских учебниках математики.
Сочинение Л. Эйлера в дальнейшем послужило фундаментом для учебников тригонометрии. Одно из первых руководств, «Сокращённая математика» С. Румовского (1760), отдел «Начальные основания плоской тригонометрии», начинает изложение следующим образом: «Тригонометрия плоская есть знание через Арифметические выкладки сыскивать треугольники, которые геометрия черченьем находит». Всё изложение сводится к решению треугольников (самые простые случаи), вычисления проводятся весьма сложным путём, учение о функциях отсутствует.
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.[25]
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (1707 – 1783). Эйлер стал рассматривать значения тригонометрических функций как числа – величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи 
. Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н.И. Лобачевского.
Современная точка зрения на тригонометрические функции как на функции числового аргумента во многом обусловлена развитием физики, механики, техники. Эти функции легли в основу математического аппарата, при помощи которого изучаются различные периодические процессы: колебательные движения, распространение волн, движения механизмов, колебание переменного электрического тока. Как показал Ж. Фурье (1768 – 1830), всякое периодическое движение с любой степенью точности можно представить в виде суммы простейших синусоидальных (гармонических) колебаний. Если в начале развития тригонометрии соотношение 
лишь выражало зависимость между площадями квадратов, построенных на сторонах переменного прямоугольного треугольника с гипотенузой равной 1, то в последующем это отношение стало отражать также сложение двух колебательных движений с происходящей при этом интерференцией.
Таким образом, на первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное и столь же важное значение имеет изучение свойств тригонометрических функций. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн.
В этот период даны обобщения многим терминам тригонометрии и, в частности, выведены соотношения для 
, где n – натуральное число, и др. Функции 
и 
рассматриваются теперь как суммы степенных рядов:
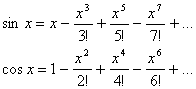
Почти также изложен и учебник В. Никитина и П. Суворова.
Вполне научное изложение тригонометрии даёт акад. М. Е. Головин в своём учебнике «Плоская и сферическая тригонометрия с алгебраическими доказательствами», 1789. В этой книге можно найти все важнейшие формулы тригонометрии почти в том виде, в каком принято излагать их в XIX в. (за исключением обратных тригонометрических функций). Автор не нашёл нужным загромождать изложение введением секанса и косеканса, так как эти функции в редких случаях применяются на практике.
В 1804 г. выходит учебник Н. Фусса. Книга предназначена для гимназий. «Плоская тригонометрия,— говорит автор,— есть наука, имеющая предметом из трёх данных и числами изображённых частей прямолинейного треугольника определять три прочие его части». Учебник состоит из 4 равных частей. Общие понятия, решение треугольников, приложение тригонометрии к практической геометрии и геодезии и, наконец, теорема сложения. Учебник Н. Фусса отмежёвывается от сферической тригонометрии.
Шаг вперёд делает академик М. В. Остроградский в 1851 г. В своём конспекте по тригонометрии для руководства в военно-учебных заведениях он выступает как сторонник определения тригонометрических функций, на первом этапе их изучения, как отношений сторон в прямоугольном треугольнике с последующим обобщением их определения и распространением его на углы любой величины. [24]
Похожие работы
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
0 комментариев