Этапы развития тригонометрии как науки
Содержание и анализ материала по тригонометрии в различных школьных учебниках
Роль и место тригонометрических уравнений и неравенств в ШКМ
Однородные уравнения
Тригонометрические неравенства и методы их решения
Метод интервалов
Основные умения, необходимые при решении тригонометрических уравнений и неравенств
Группу составляют тригонометрические уравнения, способ решения которых основан на определениях и некоторых свойствах тригонометрических функций
Решение неравенства с помощью круга
Учащиеся не уделяют должного внимания определению области применимости некоторых формул и правил;
Сравнение результатов тестирования до и после эксперимента позволяет представить их в графической форме
Навигация
Сравнение результатов тестирования до и после эксперимента позволяет представить их в графической форме
Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа
89437
знаков
1
таблица
28
изображений
2. Сравнение результатов тестирования до и после эксперимента позволяет представить их в графической форме.
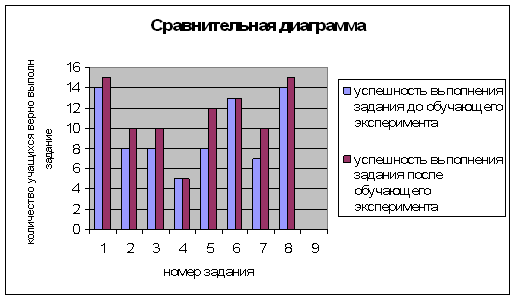
Работа с учащимися по формированию осознанного и качественного научения решать тригонометрические неравенства прошла успешно. Об этом свидетельствуют:
· Улучшение результатов проверочных работ
· Отношение самих учащихся к проведённым занятиям.
Школьники с интересом принимали участие в процессе обучения.
Таким образом, цель эксперимента достигнута. Его результаты удовлетворительны. Данная методика имеет возможность применения на занятиях по алгебре и началам анализа в общеобразовательной школе.
Заключение
Проработав соответствующую психолого-педагогическую и методическую литературу по данному вопросу, очевидно, сделать вывод о том, что умение и навыки решать тригонометрических уравнения и неравенства в школьном курсе алгебры и начал анализа являются очень важными, развитие которых требует значительных усилий со стороны учителя математики.
Таким образом, учитель сам обязан в достаточной мере владеть методиками формирования умений и навыков решать тригонометрические уравнения и неравенства. С учётом того, что тригонометрические уравнения и неравенства разделяются на несколько типов, то соответственно и методика для каждого типа различна.
Бесспорно, достичь поставленной цели с помощью только средств и методов предложенными авторами современных учебников, практически невозможно. Это связано с индивидуальными особенностями учащихся. Ведь в зависимости от уровня их базовых знаний по тригонометрии выстраивается линия возможностей изучения различных видов уравнений и неравенств на разных уровнях.
С решением уравнений, в которых переменная входит под знак одной или нескольких тригонометрических функций, так или иначе связаны многие задачи тригонометрии, стереометрии, физики и др. Процесс решения таких задач как бы синтезирует в себе практически все знания и умения, которые учащиеся приобретают при изучении элементов тригонометрии. Поэтому учитель сталкивается с довольно сложной проблемой выделения тех идей изучаемого материала, которые лежат в основе способов решения рассматриваемых задач, с целью их последующего обобщения и систематизации. Это важно и для осознанного усвоения учащимися теории, и для овладения некоторыми достаточно общими способами решения математических задач. Следует также заметить, что решение тригонометрических уравнений не только создает предпосылки для систематизации знаний учащихся, связанных с материалом тригонометрии (например, свойства тригонометрических функций, приемы преобразования тригонометрических выражений и т.д.), но и дает возможность установить действенные связи с изученным алгебраическим материалом (уравнение, равносильность уравнений, виды алгебраических уравнений, способы их решения, приемы преобразования алгебраических выражений и т.п.). В этом состоит одна из особенностей материала, связанная с изучением тригонометрических уравнений.
Другая особенность – в исключительном разнообразии таких уравнений. Именно это разнообразие влечет определенные трудности в их классификации; его следствием могут быть и затруднения в решении тригонометрических уравнений, в частности, - в выборе того приема, который целесообразно применить для получения искомого множества значений переменной.
Указанные особенности должны быть учтены учителем при разработке методики обучения школьников решению тригонометрических уравнений.
Тригонометрические уравнения и неравенства занимают достойное место в процессе обучения математики и развитии личности в целом.
Литература
1. Аджиева А. Тригонометрические уравнения // Математика. Приложение к газете «Первое сентября» № 33, 2001г.
2. Адрова И.А., Ромашко И.В. Модульный урок в X классе по теме «Решение тригонометрических уравнений» //Математика в школе. 2001. №4. С. 28-32.
3. БашмаковМ.И. Алгебра и начала анализа. 10-11. Учебное пособие для 10 – 11 кл. средней школы. М. Просвещение, 1998. – 335 с.: ил.
4. Водинчар М.И. и др. Метод концентрических окружностей для систем тригонометрических неравенств //Математика в школе. 1999. № 4. С. 73-77.
5. Гилемханов Р.Г. Освободимся от лишней работы (при решении однородных триг.уравнений) //Математика в школе. 2000. № 10. С.9
6. Зайкин М.И. Развивающий потенциал математики и его реализация в обучении (сборник научных и методических работ, предоставленных на региональную научно-практичечскую конференцию).М.: Арзамас, 2002. - 334с.
7. Зандер В.К. О блочном изучении математики / на примере изучения темы «Решение тригонометрических уравнений и неравенств» //Математика в школе.1991. № 4, С.38-42.
8. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения //Математика в школе. 1995. № 2. С.23-33
9. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ) //Математика в школе. № 3, С.18-27.
10. Золотухин Е.П. Замечания о решении уравнений вида asinx+bcosx=c //Математика в школе. 1991. № 3. С.84.
11. Калинин А.К. О решении тригонометрических неравенств. // Математика. Приложение к газете «Первое сентября» № 6, 1991г.
12. Кириченко Т.Ф. и др. Методические рекомендации для студентов-заочников по решению математических задач. Ленинград, 1987 – 53 с.
13. Клещев В.А. Обобщение метода интервалов на тригонометрической окружности //Математика в школе. 1992. № 6. С. 17-18.
14. Колмогоров А.Н. и др. Алгебра и начала анализа: Учебное пособие для 10 – 11 кл. средней школы. М. Просвещение, 1998. – 335 с.: ил.
15. Кордемский Б.А. Как увлечь математикой. М.:Просвещение, 1981. -112с.ил.
16. Е.И. Лященко и др. Методические рекомендации по формированию ведущих понятий курса математики. Ленинград, 1988. – 72 с.
17. Мирошин В. Отбор корней в тригонометрических уравнениях.// Математика. Приложение к газете «Первое сентября» № 17, 2006г.
18. Мордкович А.Г. Беседы с учителем. М.: ООО “Издательский дом “ОНИКС 21 век”:ООО “Издательство “Мир и Образование”, 2005”
19. Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.: Учебник для общеобразовательных учреждений. – М.: Мнемозина, 2000. – 336с.:ил.
20. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной школе // Математика в школе. 2002. №6.
21. Немов Р.С. Психология: Учеб. для студ. высш. пед. учеб. заведений: В 3 кн–4-е изд. М.: Гумакнит. изд. центр ВЛАДОС, 2003.-Кн.1:Общие основы психологии.-688с.
22. Немов Р.С. Психология: Учеб.для студ.высш.пед.учеб.заведений: В 3 кн. – 4е изд. М.:Гумакнит.изд.центр ВЛАДОС, 2003.-Кн.2: Общие основы психологии.-608с.
23. Орлова Т. Решение однородных тригонометрических уравнений: Конкурс “Я иду на урок” //Математика. Приложение к газете «Первое сентября» № 48, 1999г.
24. Пичурин Л.Ф. О тригонометрии и не только о ней: М. Просвещение, 1985г.
25. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.
26. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений //Математика в школе. 2004. № 1. С. 24-26.
27. Суворова М.В. Повторительно-обобщающие уроки в курсе математики (на примере изучения темы «Тригонометрические уравнения» //Математика в школе. 1995. № 4. С.12-13
28. Токарева А. Тригонометрические неравенства. // Математика. // Приложение к газете «Первое сентября» № 44, 2002 г.
29. Шабунин М. Тригонометрические уравнения. // Математика. Приложение к газете «Первое сентября» № 12,13, 1995г.
30. Филатов В.Г. О потере корней при решении тригонометрических уравнений //Математика в школе. 1991. №2. С.57-59.
31. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях //Математика в школе. 2004. №1. С.20-24.
32. Якимовская И.С. Знания и мышление школьников. М.: Просвещение, 1976.
Похожие работы
... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...
... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...
0 комментариев