Метод интервалов

1.5.2 Метод интервалов

Многолетний опыт преподавателей математики убеждает, что учащиеся, успешно решающие тригонометрические уравнения, часто испытывают серьезные затруднения при решении тригонометрических неравенств, допуская много ошибок в окончательном отборе решений, после того как выполнена основная часть работы. Ошибки появляются из-за невнимательности или в силу того, что учащиеся не поняли каких-то специфических особенностей неравенства. Не помогает и проверка. Она не всегда достаточна, для того чтобы обнаружить ошибку. К тому же при наличии в ответе одного-двух интервалов проверка утомительна, а при большем количестве интервалов техническая сложность проверки многократно возрастает.

В связи с этим разработан особый методический подход к заключительному этапу решения тригонометрического неравенства, который удобно разъяснять учащимся с помощью специально составленного алгоритмического предписания.

1.  Привести неравенство к такому виду, чтобы в одной его части (например, в правой) стоял ноль.

2.  Определить нули и точки разрыва функции, стоящей в левой части неравенства.

3.  Расставить на единичной окружности точки, являющиеся представителями всех найденных чисел.

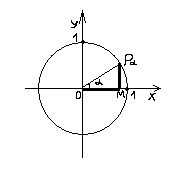
4.  Выбрать произвольное число  (значение аргумента функции, стоящей в левой части неравенства), не совпадающее ни с одним из ранее полученных чисел.

5.  Провести луч под углом  к координатному лучу Ох.

6.  На луче  получить контрольную точку . Для этого подставить число  в левую часть неравенства и определить знак получившегося выражения.

Если выражение больше нуля, то  - это произвольная точка луча , лежащая вне единичной окружности.

Иначе  - это произвольная точка луча  внутри единичной окружности.

7.  Начиная с точки  провести плавную линию так, чтобы она пересекала единичную окружность во всех отмеченных точках последовательно в порядке обхода единичной окружности против часовой стрелки. Пройдя все точки, линия должна вернуться в точку .

8.  Выбрать нужные участки конфигурации, которую образовала проведённая линия. Для этого:

Если выражение, стоящее в левой части неравенства, больше нуля, то выбрать участки фигуры, лежащие вне единичной окружности.

Иначе – выбрать те участки фигуры, которые расположены внутри единичной окружности.

9.  Отметить стрелками в положительном направлении те дуги единичной окружности, которые принадлежат выбранным участкам. Эти дуги соответствую множеству решений неравенства.

Проиллюстрируем данный метод интервалов решения тригонометрических неравенств.

Пример 1. Решите неравенство .

Приведём левую часть неравенства к виду и рассмотрим уравнение , которое равносильно совокупности уравнений: .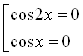

Первое из уравнений этой совокупности даёт I серию значений х: ,

Второе из уравнений совокупности приводит ко II серии .

Далее заполним тригонометрическую окружность соответствующими точками. Для I серии достаточно взять . Тогда значения  соответственно равны  (при остальных значениях n точки будут повторяться). Значения из серии  на единичной окружности можно представить точками  и , которые получены при n=0 и n=1.

Выберем теперь контрольную точку, положив . Тогда .

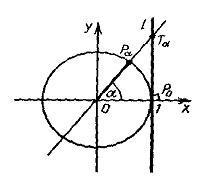
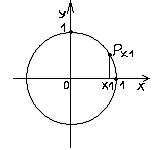
Значит, в данном случае луч  совпадает с координатным лучом Ох (угол между ними равен нулю). Выберем на луче произвольную точку , находящуюся вне единичной окружности.

Соединим точку  со всеми отмеченными точками на единичной окружности так, как показано на рисунке

Решению исходного неравенства соответствуют дуги единичной окружности в тех областях, которые отмечены на рисунке знаком « + « . При записи окончательного ответа следует иметь в виду, что в одной из областей (она показана пунктирной стрелкой) нарушается переход от меньших значений х к большим. В таком случае следует к меньшему значению  прибавить . Итак, окончательное решение можно записать в виде совокупности промежутков:

, nÎZ

Заметим, что если волнообразную линию после обхода ею всех отмеченных на единичной окружности точек не удаётся вернуть в точку , не пересекая окружность в «незаконном» месте, то это означает, что в решении допущена ошибка, а именно пропущено учётное количество корней.

Приведённый пример имеет одну особенность. Серии и  дают на единичной окружности несовпадающие точки. Если же некоторые точки разных серий совпадают, то будем называть их кратными. Точки, которые повторяются в чётном числе серий, будем называть точками чётной кратности, а те, что повторяются в нечётном числе серий, - точками нечётной кратности. Волнообразная линия, идущая от точки , после встречи с точкой нечётной кратности обязана перейти в иную область, т.е. если она находилась вне единичной окружности, то теперь будет внутри неё и наоборот. Но точка чётной кратности не даёт нашей линии возможности перейти в иную область. Поясним данный факт на конкретном примере:

Пример 2: Решите неравенство

Рассмотрим совокупность уравнений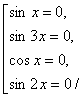Отсюда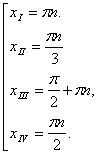

На единичной окружности значения серии представлены двумя точками 0 и . Серия  даёт точки  Из серии  получаем точки  Нанесём все эти точки на единичную окружность указав в скобках рядом с каждой из них её кратность.

Пусть теперь число  будет равным . Делаем прикидку по знаку:

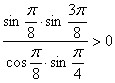. Значит, точку  следует выбрать на луче, образующем угол  с лучом Ох, вне единичной окружности. (Заметим, что вспомогательный луч  совсем не обязательно изображать на рисунке. Точка  выбирается приблизительно). Теперь от точки  ведём волнообразную непрерывную линию последовательно ко всем отмеченным точкам. Причём в точках  наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь неё. Подойдя к точке линия возвращается во внутреннюю область, так как кратность этой точки чётная. Аналогично в точке (с чётной кратностью) линию приходится повернуть во внешнюю область. Итак, мы начертили некую картинку.

Она помогает нам выделить на единичной окружности искомые области. Они обозначены знаком « +».

Окончательный ответ запишем в виде совокупности неравенств:

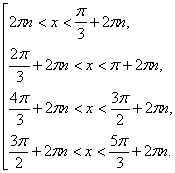
[13,c.17-18]

Глава 2. Формирование умений и навыков решения тригонометрических уравнений и неравенств

Похожие работы

Методика преподавания темы "Тригонометрические функции" в курсе алгебры и начал анализа

Скачать

73526

4

6

... комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями ...

Методика решения иррациональных уравнений и неравенств в школьном курсе математики

Скачать

98604

5

19

... проведении исследования были решены следующие задачи: 1)  Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...

Решение уравнений и неравенств с использованием свойств функций на элективном курсе по математике в старших классах общеобразовательной школы

Скачать

90068

3

1

... курс «Решение уравнений и неравенств с использованием свойств функций» Глава II. Разработка элективного курса «Решение уравнений и неравенств с использованием свойств функций» §1. Методические основы разработки элективного курса   Пояснительная записка. Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и ...

Формирование понятия комплексного числа в курсе математики средней школы

Скачать

108758

0

1

... учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала ...