Об одном подходе к решению нелинейных вариационных задач

3.6. Об одном подходе к решению нелинейных вариационных задач

В отличии от метода Ритца, искомую функцию в двуточечной вариа­ционной задаче зададим в виде:

r-^^f^-^^

При этом граничные условия и{а ) = А, ^• (б/=- /З выполняются, а ^ является искомым параметром. Решим этим методом пример из пункта 3.3.

Имеем:

Г-°\^ ^ - ^х ^^е - ^^j]Т^)^Г^-^^^^ -j^-w

л/

Минимальное значение функционала J соответствует минимальному значению функции У/о^ . Найдем /^»г- •f(<jL) :

pi fi}-rAU\' + ( -L_}' - ^=^L - J:__ .п ^ <^-Ь^-/^' [^^М ~ ^о/-/;^ (л^)^ ~~⁰^

(^ ^^)(^)^(&^)^^\^^^^/^-^ п

Так как -^^У^^/^^и A f^V^ -^W^<9 то корень уравнения нахо-дится в промежутке [1;1Д]. Представим (*) в виде </=с/-^ ^ -f^f^^^M из условия fttd)c(^W)^ ^ ^X^/,'f получим С. =-0,01.

Поэтому сходящийся алгоритм будет:

с4 ^ = о4 - оо< (((( ^ i-^)^ ~ ^)^ - ^4 - /) ^

Берем Лу =1,05 и по формуле {**) последовательно вычислим о/< =1,04256,....., ^=1,03004, о4=1,02991, с/^= 1,02990. Поэтому примем ц/^ 1,0299 ^1,03; тогда решение будет:

^а.^е^^^

51

Решение по предложенному методу и методу Ритца почти совпадают:

	0	0,2	0,4	0,6	0,8	1
	0	0,2111	0,4166	06166	0,8111	1
	0	0,1906	0,3902	0,5968	0,7981	1

Итак, предложенный подход к решению задач может быть применен, т.е. ему посильны и нелинейные задачи.

В частности, рассматривая нелинейную вариационную задачу на

отыскание ги-^ п- функционала

^/-

У /У^А7 - / f/^ ^y)ol^

с краевыми условиями ^/о^= с? ; у /"•/) -= У ;

будем отыскивать решение на кривой ^ -^ ^ ^ . Тогда функцио­

нал примет вид:

У-J/: (J, ^-') \ я^^^/Г^-г:^ х. ^JA =

.f^^L, ^ W-^с^^.,W ( ^-^ -й^-7/д if.i.ci-')

и задача об определении его л^л. сводится к отысканию пъС ^1{oi)

га). ^=^,. ^ -^ - ^; т - ^,

-Г(^)^; f"(^)^o:

Поэтому при</= ¹¹^- //<4/примет наименьшее значение на кривой и-, r^^-wm g ^^ у , азначение ^ ^/^1^1,183.

52

3.7. К методу Ритца для двумерных задач

Для функционала •^- ^J '( ^v-' ^ ^^Р^)^ <^ уравнение Эйлера- Лагранжа примут вид:

JiL-iL^l-.-S-/2L ^ ^ъг-ъг ъ^\ър) осЛм / ^5где ?~ ^эх '

^ ^-? ⁼ ^ •

Пусть ищется экстремум функционала

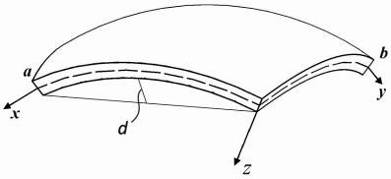
f[:iC^n-J[h^^- г<^-?^4 .средифунк-ций, обращающих в нуль на границе квадрата, ограниченного прямыми dc^^-f •> с/ = ± d • При этом мы приходим по существу к задаче Дирихле для уравнения Пуассона ^ у. у- i^y ="У С^^}^

г^;Г^г^/;/^ ^/;-/^г^-/;~/;=<9 (см.рис.12)

Эта классическая задача не решается | точно с помощью элементарных функций. Приближенное решение ищем при ^(у/^)~=^ —^<———— ———*7⁷"^.

по методу Ритца в виде i-i ^f^~^)('f~^²'} Подстановка в исходный функционал дает •

f^f[W(^ ^^Г. ^ ^.г.с(^х^}}Л^. ^j-^ ^с^-Г^)

Тогда Г1^)-^-^С- ^---0- С--^ :

ПФ^-^о, ^ у ^ ^й=-^, u—ig(^)W

решение задачи при первом приближении.

Сравнение с точной формулой (имеющий вид бесконечного ряда) показывает, что погрешность этого приближенного решения в среднем равна 1,5%, а погрешность в значении функционала около 0,2%. Таким об­разом, идея метода Ритца распространяется для двумерных (и, вообще, для многомерных) задач.

53

ЗАКЛЮЧЕНИЕ

Дипломная работа посвящена методам решения экстремальных за­дач, при этом приведены основные идеи различных методов, которые поч­ти совсем не рассматриваются в школьном и педвузовском курсе матема­тики. Таким образом, заполнен существенный пробел в математическом образовании и подготовлен материал для изучения основ современной прикладной математики в классах с углубленным изучением математики.

Основные выводы по дипломной работе:

1. В краткой реферативной форме изложены элементарные методы решения экстремальных задач, основанные на известных неравенствах ти­па Коши.

2. Приведены основные идеи методики решения задач математиче­ского программирования: три разновидности задач линейного программи­рования, принципиально различные примеры решения задач нелинейного программирования.

3. Изложены методы решения двухточечной краевой задачи; дан вы­вод сходящегося алгоритма и на его основе решены на ЭВМ ряд линейных задач с переменными коэффициентами.

4. Излагается вариационная задача с выводом уравнений Эйлера-Лагранжа и на их основе приводятся примеры аналитического решения. На основе идей метода конечных разностей получен алгоритм для линейной вариационной задачи и на его основе решены ряд вариационных азадач на ЭВМ; результаты приведены в приложениях.

5. Методом Ритца решены ряд нелинейных задач, одна двумерная за­дача. На основе решения модельных задач подтверждается достоверность полученных результатов.

6. Приведена новая модификация метода Ритца, для которой нели­нейность вариационной задачи не вызывает особых затруднений.

ЛИТЕРАТУРА

1. Алгебра и начала анализа 10-11 кл., М., 1992.

2. Белман Р., Калаба Р. Квазилинеоризация и нелинейные краевые задачи. "Мир", М., 1968.

3. Блох В.И. Теория упругости. Харьков, изд-во ХГУ, 1964.

4. Буслаева И.П. Решение задач без использования производной. Матема­тика в школе № 5 -1995.

5. Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы. М., 1985, "Просвещение".

6. Данко П.Е., Попов А.Г., Кожевникова Г.Я. Высшая математика в упражнениях и задачах. М., "Высшая школа", 1986.

7. Демидович Б.П., Марои И.А., Шувалова Э.З. Численные методы анали­за. М., "Наука", 1967.

8. Дородницын А.Р. Применение малого параметра к численному реше­нию дифференциальных уравнений. В книге "Современные проблемы систематической физики и вычислительной математики". "Наука", М., ^ 1982.

9. Камке Э. Справочник по обыкновенным дифференциальным уравне-« ниям .- "Наука", М., 1972.

10. Краснов М.Л., Макаренко Г.И., Киселев А.И. Вариационное исчис­ление. "Наука", М., 1967.

11. Курант Р. Курс дифференциального и интегрального исчисления. "Наука", М., 1967.

12. Матвеев И.М. Дифференциальные уравнения. "Наука", 1970.

13. Мышкис А.Д. Лекции по высшей математике ."Наука", М., 1969.

14. Сайфуллин Э.Г., Саченков А.В., Тимербаев P.M. Основные уравнения теории упругости в напряжениях и перемещениях. Сборник исследова­ний по теории пластин и оболочек, в. 18, часть 1. Казань, Изд. КТУ, 1985.

15. Соминский И.С. Элементарная алгебра. Дополнительный курс. Физ-матгиз, М., 1969.

16. Циаф Л.Я. Вариационное исчисление и интегральные уравнения.

"Наука", 1970г.

t„ 17. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчис­ление. "Наука", 1969.

• ^. "

HWUA-cA^ /^1СЛ^И-1с^«^-''1Д.

program diplomi; 4.

uses graph,crt;

label 1;

const n=200;

type mas=array[0 ..n]of real;

var a,b,c,d,f,y,p,xx,l,r,g: mas;

j,z,x,h: real;e: char;

i,j1,il: integer;

ff:text;

procedure vap(var xx,y : mas) ; клил-ели.^- бор-с.(,ои/^с^<^о^

var x,h: real; i: integer; ' ^с^-оли,

a,b,с,d,f,p:mas;

begin

h: = 2/n; x: =1;

for i: =0 to n do

begin

f[i]:= exp(-x*x) ;

p[i]: = cos(x*x);

xx[i]: =x;

x: =x+h end;

УСО].- =0;y[n]: =4;

for i: =1 to n do a[i]:=2+h*h*f[i];

b[l]:=y[0]-h*h*p[l];

b[n-l]: =y[n]-h*h*p[n-l];

for i: =2 to n-2 do b[i]: =-h*h*p[i];

c[l]: =a[l]; d[l]: =b[l];

for i:=2 to n-1 do

begin

c[i3: =a[i]-l/c[i-l];

d[i]: =b[i]+d[i-l]/c[i-l];

yCn^l]: =d[n-l]/c[n-l];

for i:=2 to n-1 do

y[n-i]: =(d[n-I]+y[n-i+l])/c[n-i];

end ;

procedure kr( var xx,y :mas); ьтшлмлла ^Uscuiocd \gjqcuwl var x,h: real;!: integer; ' ^vv a,b,c,d,l,r,p,g,f: mas;

begin

h: =l/n; x: =0;

for i: =0 to n do begin

p[i]: =2*x;

g[i]: =x*x;

f[i]: =sin(x*x);

xx[i]: =x;

x: =x+h;

У[0]: =0;y[N]: =3;b[l]: =y[0]-2*h*h*f[l]/lCl];

cCl]: =a[l];d[l]: =b[l];

for i: =1 to n-1 do begin 1[i]: =2-h*p[i];

a[i]: =(4-2*h*h*g[i])/l[i];

r[i]: =(2+h*p[i])/l[i];

end;

for i: =2 to n-1 do begin c[i]: =a[i]-<r[i-l]/c[i-l]);

b[i]: =-2*h*h*f[i]/l[i];

d[i]: =b[i]+(d[i-l]/c[i-l]);

end;

for i: =1 to n-1 do

у [n-i]: =<d[n-i]+r[n-i]*y[n-i+l])/c[n-i];

end;

begin il: =detect;initgraph(il,j1,'' );

assign(ff,' b: reseda, dip' ); <2. rewrite(ff);

1: cirscr; settextstyle(0,0,2);

outtextxy(300,80,'МЕНЮ: ' );

outtextxy(135,150,'1.РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ.');

outtextxy(135,200,'2. РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.'):

outtextxy<135,250,'3. КОНЕЦ . ' );

outtextxy(145,350, 'ВЫБЕРИТЕ НУЖНЫЙ ПУНКТ МЕНЮ .');

Е: =READKEY; •

case e of ' Г: begin

cirscr;settextstyle(0,0,3);

outtextxy(100,40,'РЕШЕНИЕ ВАРИАЦИОННОЙ' );

outtextxy(250,80,'ЗАДАЧИ' );

settextstyle(0,0,2);

outtextxy(155,130,'Дана вариационная задача:');

outtextxy(145,200,' I(Y)= ( y+2cos(x)y+e y )dx');

settextstyle(0,0,4);outtextxy(230,190,'S');

settextstyle(0,0,2);

outtextxy(200,280,' y(l)=0 , у(3)=4 ');

settextstyle(0,0,2);

outtextxy(240,170,' Г );outtextxy(235,225,'3');

SETTEXTSTYLE(0,0,1);

outtextxy(329,190,'2');

settextstyle(0,0,2);outtextxy(315,180,',');

settextstyle(0,0,1);

outtextxy(440,190/ 2');

outtextxy(500,190,'-x');outtextxy(520,185,'2');

vap(xx,y); writein;

writeln(ff,' РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ' )

writeln(ff);writeln(fr);i: =0;

while i<=n do begin

if i<=n then

writeln(ff, ' ' ,xx[i]: 1: 3,' \ ',y[i]:l:3, ',xx[i+l]: 1: 3,' ',y[i+l]:1:3)

© 1 S6

writeln(ff,' ' ,xx[i]: 1: 3,' -,y[i]:l:3);

i: =i+2; end;

e: =readkey; goto 1; end;

'2': begin

cirscr; SETTEXTSTYLE(0,0,3);

OUTTEXTXY( 50, 80, '-РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ.');

settextstyle(0,0,2);

OUTTEXTXY(150,130,'Дана краевая задача: ');

OUTTEXTXY(145,200,'y+2xy+xy=sinx ' );

OUTTEXTXY(150,280,' y(0)=0 , у(1)=3 ');

OUTTEXTXY(152,180,' ,,' );

OUTTEXTXY(218,180,' ,' );settextstyle(0,0,1);

OUTTEXTXY(255,190,'2' );

outtextxy(350,190,'2');

kr(xx,y); writein;

writeln(ff,' РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ' );

writeln(ff);writeln(ff);i: =0;

while i<=n do begin

if i<=n then

writeln(ff,' ',xx[i]: 1: 3,' ',y[i]: 1: 3,

',xx[i+l]: 1: 3,' ' ,y[i+l]: 1: 3) else

writeln(ff,'  ' ,xx[i]: 1: 3,' ',yCi]: 1: 3);

i: =i+2; end;

e: =readkey; goto 1; end;

.' 3': begin

cirscr;

settextstyle(0,0,2) ;

outtextxy(150,280,'нажмите на любую клавишу ') ;

E: =readkey;

closegraph ;

end;

end;

close(ff);

end.

program diplom; <5 const n=200;

type mas=array[0. . n]of real;

var a,b,c,d,f,y,p,xx,1,r,g: mas;

x,h,jl,yl,j2,y2: real;

i: integer;

ff: text; „ о procedure vap(var xx,y :mas); рвит^шло. Ьсир<лсцш^У<мо^ var x,h: real; i: integer; f,p, a,b, c,d: mas; ^Cc^c^cc begin h: =2/n; x: =0;

for i: =0 to n do begin

f[i]: = -1 ;

p[i]: = 0;

xx[i]: =x;

x: =x+h end;

y[0]:=0; y[157]:=l;

for i: =1 to 157 do

a[i]:=2+h*h*f[i];

b[l]:=y[0]-h*h*p[l];

b[156]: =y[157]-h*h*p[156];

for i: =2 to 157-2 do

b[i]: =-h*h*pCi];

c[l]:=a[l]; d[l]:=b[l];

for i: =2 to 157-1 do begin

c[i]: =a[i]-l/c[i-l];

d[i]: =b[i]+d[i-l]/c[i-l];

end;

y[156]: =d[156]/c[156];

for i: =2 to 156 do

y[157-i]: =(d[157-I] +y[157-i+l])/c[157-i];

end;

procedure kr(var xx,y :mas); р>влллели,<Л. ^сиг-С^Сл! ^wo^m.

var x,h: real;i: integer;a,p,g,f,r,1,b,c,d: mas; ^/</

begin

h: =2/n; x: =0;

for i: =0 to 100 do begin

P[i]:=0;

g[i]: =0;

fCi3: =x;

xx[i]: =x;

x: =x+h;

end;

У[0]: =0; y[100]: =1;

for i: =1 to 100 do begin

1[i]: =2-h*p[i];

a[i]: =(4-2*h*h*g[i])/l[i];

r[i]: =(2+h*p[i])/l[i];

end;

b[l]: =y[0]-2*h*h*f[l]/l[l];d[l]: =b[l];c[l]: =a[l];

for i: =2 to 99 do begin

- b[i]: =-2*h*h*f[i]/l[i];

c[i]: =a[i]-<r[i-l]/c[i-l]);

d[i]: =b[i]+(d[i-l]/c[i-l]);

end;

у[99]: =(d[99]+r[99]*y[100])/c[99];

for i: =2 to 99 do

yClOO-i]: =(d[100-i]+r[100-i]*y[100-i+l])/c[100-i];

end;

begin assign(ff,' b: res.dip');

rewrite(ff); writeln(ff); ^ vap(xx,y);

writeln(ff,' РЕШЕНИЕ ВАРИАЦИОННОЙ ЗАДАЧИ');

writeln(ff);

i: =0;jl: =0;

writeln(ff,' численное решение',

','аналитическое решение');

writeln(ff);

while <i<=157) and (jl<=1.57) do begin

yl:=sin(jl);

writeln(ff,' ',xx[i]: 1: 2,' ',y[i]:l:3,

',J1:1: 2,' ' ,yl: 1: 3);

i: =i+l;jl: =jl+0. 01; end;

I writeln(ff,' ' ,xx[157]: 1: 2,' ' ,у[157]:1: 3, ',J1:1: 2,' ' ,yl: 1: 3);

writeln(ff);

kr(xx,y);

writeln(ff);

writeln(ff,' РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ' );

writeln(ff);i: =0;j2: =0;

writeln(ff,' численное решение',

' /аналитическое решение' );

writeln(ff);

while (i<=100) and (j2<=l) do begin

y2: =j2*j2*j2/6+(5>Kj2/6);

writeln(ff,' ',xx[i]:1: 2_,' ' ,y[i]:1: 3, ' ,j2: 1: 2,' ',у2: 1: 3);

i: =i+l;j2: =j2+0. 01; end;

writeln(ff,' ',хх[100]: 1: 2,' ',у[100]:1: 3, ' ,з2: 1: 2,' ' ,у2: 1: 3);

close(ff);

end.