I (ol-i-x)c 6+Х-}
Экстремальные задачи в неполной средней школе
Л. Транспортная задача линейного программирования
Задача о рационе
Понятие о задаче нелинейного программирования
Понятие о краевых задачах
Приближенный метод решения краевых задач. Конечно-разностный алгоритм
Постановка простейшей задачи
Метод Эйлера в вариационной задаче
Алгоритм решения линейной вариационной задачи
Об одном подходе к решению нелинейных вариационных задач
Навигация
Понятие о задаче нелинейного программирования
К решению нелинейных вариационных задач
57698
знаков
75
таблиц
8
изображений
1.7.4. Понятие о задаче нелинейного программирования
Рассмотрим примеры решения простейших задач нелинейного программирования.
Пример 1. , Найти минимальное и максимальное значения функции ^= (^ ~^) + (3^ "^ ) при ограничениях С X/-^ Хл. >- ^ \ -?гс< +3^1 ^{2 L лу s^, эс^^О
Решение:
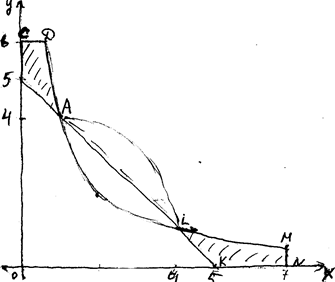
Область допустимых решений представляет собой многоугольник АВСЕ (рис.3). Проводя из точки М, как из центра, окружности различных радиусов, получим: минимальное значение функции г (SZ>)=196/13 принимает в точке Ю (24/13, 36/13), в которой окружность касается области решений. Точка ^) не является угловой, ее координаты находят решая систему уравнений, соответствующих прямым /Йс> и C£~ . Имеется два локальных максимума: з ( д\ = (f-^)^ + (о-б)2 = ^•5' ;
i(^}-- C&-^)2 + (о~б)2 = Ю
| 6 . ^ рис.3 Пример 2 Пусть область допустимых решений остается прежней, а й-s (,Т/-^) ^ -<- ( ^й~^)2 найти минимум и максимум i . Решение: |
| Так как | 2M> i | (е) | , то вершина А есть точка глобального мак- | ||||
| симума. | \. | • | —- | — — | ---^м | ||
| - | / 1 | ||||||
| / | |||||||
| f- | is, | / | |||||
| н | \^ ^ | ||||||
| • ^ | s | / | |||||
| ,'' | \ | ( | |||||
| <2> | |||||||
| /' / | • ':; ' •-- г | ||||||
| / | ^. 1 | ||||||
| / | // | ||||||
| / | / / | ||||||
| у | |||||||
| в | / | ||||||
| f | \ | f / | / / / \>•~- | ||||
| \ | .А | Г4 | .—^-^- | ||||
| б | Г л | ч | 6 -^ | '> | |||
26
Минимальное значение функция принимает в точке A<i(4;l),
iW=0. , , -
I: г^с^ i = i( e)- zfe;o) =-^
II: ^а^ г ^ ^fe; - ^" ; глобальный /^wc г = гЛ?; ^)^/c)^2S.
ПримерЗ
Найти максимум и минимум значения функции i ~- Vf
при ограничениях: ( Xr- 3Q. ^^
\ зе^^^-S , ^ ?^ ^г^)
(^ У, ^ Ч, Жг ^6'
Решение:
В этом случае (рис.4) область допустимых решений не является выпуклой и состоит из двух отдельных частей, fnin. 2= i (^(-/;^)) = i(L(^^))-=^y I. ^лх i-- i (^ r-^;6'J; -~ ^/9
II.
Точка М (7;4/7) - есть точка глобального максимума
|
|
Н
Общая задача математического программирования формулируется следующим
образом:
\f1 f \ найти вектор: л С ^ / ^у
координаты которой удовлетворяет системе ограничений: д
^(^,.,^=^, ^'^/2,...,,С ^ (Х,,...,^]'=^, i^^f,...,n-
Н и доставляющий экстремум __ ^ э. функции i^ f('x^..., х^).
1 ^ ^ 7^
Рис.4
В настоящее время (начиная с 1950-х годов), бурно развиваются методы решения задач математического программирования с привлечением современной вычислительной техники.
27
II. О КРАЕВЫХ ЗАДАЧАХ
Похожие работы
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
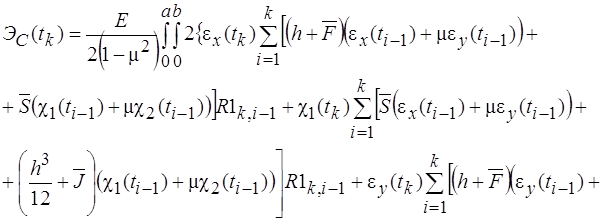
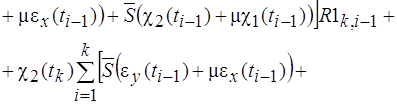
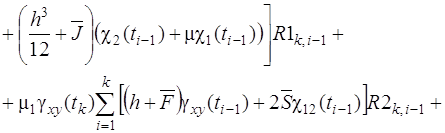
0 комментариев