Постановка простейшей задачи

3.1. Постановка простейшей задачи

Задача состоит в определении функции и •=. •? ('>-) , которая со­общает экстремальное значение некоторой величины У= ^У^у7 , т.е. функционала, ^г.

Предположим, что ^ J р ^ у. /) ^ ^

7<

^^х'^^; ^^ (1)

где г (. ^эе/ у, ^/ - заданная функция, и а - заданные числа.

У^

Различным кривым ц : и [ ^е.) , проходящим через граничные точ­ки С эс<; ^ ) и (^л.', Уи.) , будут отвечать различные величины. Определим такую функцию у ^ i/ С^) , для которой ^ i- ^'('^У'^ , т.е. функционал принимает максимальное или минимальное значение. Да­лее будем рассматривать задачу только на минимальное значение УГ^'(>)], т.е. будем искать такую функцию у= уЛ^ , чтобы было

Н^(^).] '- ^^п- ^Су(^)] ^ Л³^ Х^Х^ . Например, для задачи

п^- JYy'^ ^х, ^о)--о, ум^ (&)

/ функции i/ =- х. , ol 6r [p, будут удовлетворять условиям :

ylo)^o, ^}--L

При этом .,

г / ^

У г,. ^ - Я U^) ^ ^)^. ^ ^ ^-. fU).

33

задача свелась к нахождению минимума обычной функции -fW:

n'J) - ^^°⁶ А__ /,

^\{^~~^^~ ~^^ ^⁰ -

(^^)(^1)^-2-(2^-Y)^0 ^

U -г) (^³^ з^ ^ з^ + /) ^о -7 о^ = ^.

Нетрудно показать, что при +{2) ^ /^-п г(⁰^/ ^ Итак, ь.^ -УГ^-^^,-^0^ ^^> ^ З";

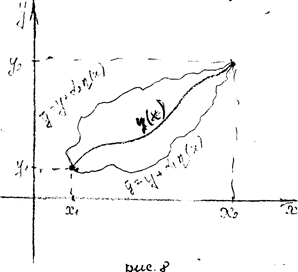
решение задачи будет: и=- ое^' Рассмотрим семейство кривых (см.рис.8):

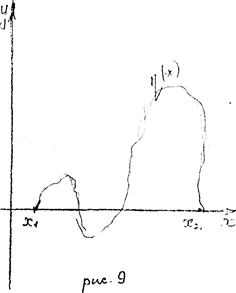
у f^ jc^ = y^ + с/. ^ ^  , где ^ ^ -произвольная функция, но ц (зе^)^ И (v.s.}~-C> (см .рис. 9).

'.( - i A

Тогда при малых об для кривых L/(o[^oc,) интеграл (1) будет принимать значения близкие к минимальному и зависит от параметра^:

.Vi

(з)

Если мы предположим, что функция у^ доставляет минимум J^v, то необходимое условие минимума будет: ^/,

oL-JW

^^ ^

Продифференцируем (3) по Л:

dl. ? d^d-r,- Тг ^C)F •^ ^ ^эр •^7,/

~си ~ J ^г^-J l &r й-⁺ у cSrJ^ ~-

я< yf ^q v

~- t^rt^rt'^-

34

Имеем:

.Г;. ^

JVt>^- i^^

Л'« JC< -ха /^2г

- Fn' • v ^ - ( ^

Поэтому:

^ - ( Г F' ^ F' 7 и/ )У

^^-J Lf^^^J^)^-

л/

-h^ri.-^^^o ®.

'VI.

/ ®

Законность перехода —-^ обуславливает следующая основная лемма вариационного исчисления:

Если Ф(^) , ^) непрерывны на JZ У<; % 7

и^Н^-^ то из

У

J^?^^A^--^

вытекает, что ^(ус) = <9 при ^ ^ у ^ СР^ .

35

Доказательство (от противного). _ _ Пусть ^(^^О ^ ^(^)7У>0 при Л^^ж^з^

ПОЛОЖИМ ({X.- Зй)^^- Хг) ^ "Р" Зс/^ Зе^. Д^

^ (^9С-) = ^ о при Xf ^ зе^- ДС,,, L у 5с-^ 5с ^ ^.

—t.

Тогда по свойству интегралов [ g>^L [^olx. >0

У.-1

вопреки допущению. Значит ^Р ( ^,) = О. Итак, мы пришли к следующему утверждению:

задача (1) эквивалентна краевой задаче:

^'-^ /У⁼ ° ' ^⁾^ ^⁾^ , . (5)

Дифференциальное уравнение /•?^/ - ^' F^' ~ ^u

носит название Эйлера-Лангранжа.

Решим пример (2), сводя к краевой задаче (5). ,ii . //// t:' - о,/^

Примеры аналитического решения вариационных задач

f!/l

1) ^ у. / Су-\у' -7^ - о. ^о)= о. ^W- i -

Составим уравнение Эйлера-Лангранжа:

~^-^'^-°- -^~У-° - ^-/ -

и^^и^О ^ Lf ^ C^-w эе^ gl ^ ^;

ffo )= О СО, • c^-s 0+ ^ -Л fi о = О Г ^ _

^№)^ " lc. ш^^(^-^%^1 ^ 1 e^i

Ответ: (у -. St-^i X.

²⁾ ^^;'^- J ^^ •^^/гJ^ ^ у^'^' ^ ^^;=6)

^ - (F^L -о ^ ^"^6^ ^^"^б^-о ->

и-.- х-^+Сгзс-t- G. ;

{^(^)^ (-f-C^C^-f \_^(о):о ^л- L а-о

Ответ: и = -х³

3) ^у- / (^у-^^ ^^ ^•^--^•

^-^')^о - ' ^^^-.^--^^.^^ f^)^ ГС^ . , ,

Г^г - [с^^ ' ^cf-^^

Ответ: Ут^¹^^,

-f

4) ^У" J (^-^^)d^,

^(^)--^ ^(^)--^

^^v^⁰ ^ ^^{^}-^2Э=^- ^-^-^^^^^ ;

^f-/)=^ ^' ^^-^⁼ ^ ^-ⁱ ^[^/6 ^^^^ "

^ - %

р - /-^

и ^ о

Ответ: У^ - ^Уе -* % ^{л 5}) о .

^TyJ 'J (У-i'^Jc/x ; ^-i)--0,y[o)-Z .

fy - (Fy'J^O ^ y'^x^o ^ a—^/e-'-^Kft't ;

r и(-i)^o f^ _ с, +U ^о

i^^ 'с . о^ -⁷

Г^ - ^/6

Lu ' ^

Ответ: ^ -»%+ ^^^

б) dC^-- j "^А (у' ^у/А / ^= /, ^/^Д Г^/г

^- ^^ - -^^-^^

^ (^ й^-г ^-^ С( • ^/г X. ;

^[о)-- ^у ^f^- CUS^^O •^•/г6?- ^ ^)-% ^ L^- ^^-^-^

ft-^, C^~-o

Ответ 1/' - (^^" % 7)  ^ У - ] if . 4у^^ , yfo)-e ⁱ, ^ /.

Уравнение Эйлера-Лангранжа:

^/,и^о^ fy^^y ^y^^e^^Qe

е^ f^e^e^^ Г^-^

38 2(f-^

Ответ: ^ ^е щ ⁸) ^у= / ^--^^ , ^о)-^(^)-0

Л/ - f^^ = о ^ ^с/ ^У^ ⁰ •^=> у= ^ ^^J ^ ^ ^^/1- ^ ⁷

С и{о)^ о . С С^- cpso 1- ^-^по-^о i ч (^ )^о ^ I ^ • с^злП^ G • si^s. /7= о

С ') Р ^L{=и '> ⁽- д. _ произвольное

Ответ: и ^ d ^п. х- - множество решений.

39

Похожие работы

Алгоритмы параллельных процессов при исследовании устойчивости подкрепленных пологих оболочек

Скачать

74337

5

31

... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...

Динамическое программирование и вариационное исчисление

Скачать

24366

0

0

... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования   2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...

Решение оптимизационной задачи линейного программирования

Скачать

59893

13

0

... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5).   СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...

Решение обратных задач динамики

Скачать

31691

0

25

... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...