I (ol-i-x)c 6+Х-}
Экстремальные задачи в неполной средней школе
Л. Транспортная задача линейного программирования
Задача о рационе
Понятие о задаче нелинейного программирования
Понятие о краевых задачах
Приближенный метод решения краевых задач. Конечно-разностный алгоритм
Постановка простейшей задачи
Метод Эйлера в вариационной задаче
Алгоритм решения линейной вариационной задачи
Об одном подходе к решению нелинейных вариационных задач
Навигация
Задача о рационе
К решению нелинейных вариационных задач
57698
знаков
75
таблиц
8
изображений
1.7.2. Задача о рационе
1. Поставка задачи
Пусть известно, что животному ежедневно надо выдать о^ единиц жиров В/ , ш - углеводов Вг , V, - белков В^ . Для откорма животных можно закупать 2 вида комбикормов. Единица веса первого корма dy содержит <2// единицы вещества K-f , d/г. единицы вещества В^ и <2/а единицы вещества 6э , а стоимость ее равна <?/ рубля. Для второго вида кормов данные соответственно равны 0^ , С^ц , <^гл и Сц . Требуется составить рацион, при котором была бы обеспечена суточная потребность вещества вг , при чем стоимость ее была бы наименьшей.
Все данные поместим в таблице 2.
| Виды корма | Белки | Жиры | Углеводы | Стоимость 1-й единицы |
| I | ft/< 2 | CLfz 3 | ^<з ^ | ^ |
| II | ^ / | CL^ tt | ^ f | е. |
| 6< 6 | ^3. f2 | ^ ^ |
Таблица 2
Математическая модель задачи
Пусть 1\- количество первого вида корма, х^ - количество второго вида корма, получаемого животным за сутки. Так как животное может получить питательных веществ больше нормы ^ , то очевидно:
(Ц.^^^ , '^--f^.s.
с--Г
(3)
Общая стоимость кормов, затраченных на одно животное будет:
| (4) |
т= C\x^C^Xs =
i^ W Итак, математическая задача формируется следующим образом
23
Найти неотрицательное решение системы неравенств (3), дающее минимальное значение линейной формы + = C-t з^ + Сг ^-а. . Выражение для + называют линейной формой потому, что в него не входят члены со степенями выше первой и произведением -с, и 3^.
Решение задачи (частный случай).
Пусть g/=6", 8>^f2, ^д=^ 0,^2 , Q^ ^, ^a ^/ ^ ^ gs.^ =^
CZ^i = / , С/ ^ Q 2 ^д. ^ ^ 3 , л? ^ д?/, js/ = •2?-2 .
Множество решений системы неравенств:
| ( <?^+ У >.6 2 э^ + ^у ^ ^ ^^1 + ^ ^- ^ |
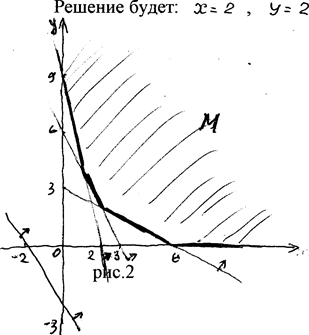
есть открытый многоугольник А - (рис.2)
Среди всех точек этого множества нужно найти такую, координаты которой минимизируют линейную форму +=с^5х+ о, -5 У . Если зафиксировать какое-нибудь значение выражения -f= С , то получим линейное уравнение с двумя неизвестными ^S-sa-O^y^c ^ график которого есть прямая. При изменении от ~т>одо оо прямая o^v.-t-Qb'd^c , смещаясь параллельно самой себе, "зачертит" всю плоскость. При некотором значении с = С/ эта прямая достигнет многоугольника М в точке В • Очевидно, в этой точке -f примет наименьшее значение. Координаты точки В, находим решив систему: Г 2 х- i-y ^ G
i <?г ^ ^ = /'<?
|
|
Итак, наименьшее значение линейной формы -/=<^5х-к^3^ в М. достигается в точке в ^г; 2) Таким образом, для наивыгоднейшего откорма животных надо брать оба вида кормов по две единицы.
24
1.7.3. Задача об оптимальном использовании сырья
1. Постановка задачи
Пусть предприятие вырабатывает продукцию двух видов П, и Лд , для чего используется сырье трех видов S<, ^ , -?э соответственно в количествах ^ , ^z. , ^.i . Для изготовления единицы продукции (^потребуется и/, , й& , ^<s единиц сырья Sf , ^г. , •5л соответственно. Условно запишем это так: П = Он S{ + Ом. 5л ч- С?/& 5д . Аналогично допускаем , что П = Ог/ ^ у- ^ -s;? + ^^ ^з . Доход, получаемый предприятием от выпуска единицы продукции Л< и Па равна соответственно Су и Сд. рублям. Требуется спланировать работу предприятия так, чтобы обеспечить наибольшую прибыль. Все данные представим в виде таблицы 3.
Таблица 3
2. Математическое описание задачи
Предположим, что нужно изготовить •3?/ единиц продукции П< и Л^ единиц продукции П^ . На это уйдет d^ Л\ + Cf^ Xa. единиц сырья J/ i. = /, 2/3 . Принимая во внимание ресурсы предприятия, можно написать:
(2// Л'< + 0.^ ^ ^ ^/ о^ О'/ + 0<.i ^ ^ ^
(2/s Я?/ + йгд ^ ^ ^з
Общий доход выражается линейной формой ^= б< а?/ + Сл. 3?г. Итак, требуется найти неотрицательное решение системы неравенств, дающее максимальное значение f^ e^ ^ -^ С^Ха. Эта
задача решается аналогично задаче о рационе.
25
Похожие работы
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
0 комментариев