I (ol-i-x)c 6+Х-}
Экстремальные задачи в неполной средней школе
Л. Транспортная задача линейного программирования
Задача о рационе
Понятие о задаче нелинейного программирования
Понятие о краевых задачах
Приближенный метод решения краевых задач. Конечно-разностный алгоритм
Постановка простейшей задачи
Метод Эйлера в вариационной задаче
Алгоритм решения линейной вариационной задачи
Об одном подходе к решению нелинейных вариационных задач
Навигация
Понятие о краевых задачах
К решению нелинейных вариационных задач
57698
знаков
75
таблиц
8
изображений
2.1. Понятие о краевых задачах
К краевым задачам дифференциальных уравнений сводятся большинство естественно-технических проблем, которые возникают при составлении математических моделей реальных процессов. Здесь Приводятся лишь основные понятия о краевой задаче (на примере двухточечной задачи) и об основных методах решения. Задача
Найти решение дифференциального уравнения Ц = х. в области о^ ос ^ / при граничных условиях ^fo)=o^^)= -f Решение: ^ Интегрируя уравнение У = х- получим общее решение -У = ^-^ ^ х-^С^ ^
| а удовлетворяя граничным условиям, получим систему: с} = о Со + С, -о^ Q = о ('с^=о • /t I . •••» ) , |
| У' i • |
| ./: |
| - г" • Рис.1 |
|
|
(Ч(с)=0 [0-Ц\Л^ t/6
Тогда решение задачи будет; У= ^^ ^ •% х-
Геометрический смысл задачи приведен на рисунке 1
Обобщение:
Рассмотрим простейшую двухточечную задачу:
Найти функцию iy= Ц (^), удовлетворяющую дифференциальному уравнению второго порядка и "^ -f(v, у, у '} ц .\ (2.1) и краевым условиям: у(а-)^ А , ^(ё)-= В.
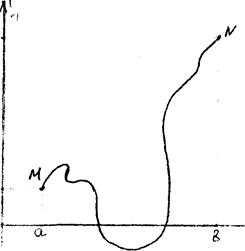
Геометрически это означает,
что требуется найти интегральную кривую уравнения (2.1),
проходящую через две данные
точки: М (л,А)^(^ Ь)
| /\ |
(см.рис. 2). На предыдущем примере мы видели, что решение
краевой задачи на последнем
этапе свелось к решению систем
уравнений. А при этом может
| Рис.2 |
возникать три случая:
1) Существует множество решений;
'2) Существует единственное решение;
3) Нет решений.
28
Различные случаи решений и постановки краевых условий приведем в следующем пункте 2.2.
2.2. Примеры .аналитического решения краевых задач
I. Пусть дано дифференциальное уравнение у '•=• - ^у и краевые условия:
а)Г^о)-(9 Q)^(o)^o вГ^^^
\^W^l Ц^П)=0 1у^2
Найдем общее решение уравнения U "i- ^и-^ с> .Ее характеристическое уравнение будет: ^^ ^-^0 и />^ = ± 2с . Поэтому :
у^ Cf сс>5 ^ус + gl s^n. S. за. . общее решение.
| С,-о 0 - ^ |
a) r^fo)=o (C}-cc5^ o^Ci-^nSO^O \и[^}^1 " \_Cf-cv^-e/^^C,L-^S-8/^S.
"7=ri / s'.^ о - единственное решение (см.рис.3).
|
|
б)С^с^о C^-co^-o^ C^-s^tS.o^o г е^о
[§Un]^o ^iCf-c^^c/l^ Gi- ^^-71-- о ^iCt-о^о
| в) |
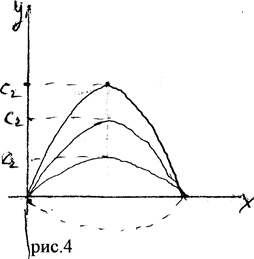
отсюда: С{ = о, С д. - любое число, поэтому множество решений будет и = Сл • •sin <3-^ (см.рис.4) - синусоиды с амплитудой Сл, .
ru^o)=o f(V- Ccss-o^- (^-^ S-o =.о (С(-С> l^W^2. ^ i^-cps^n ^ Q-5-.A-^ = 2. ^ i^ = %nS^^
| =• оо |
| , т.е. нет решения. |
| / |
| ТГ у |
| рис.3 |
| при краевых условиях: |
II. Решить уравнение ^ - 5^ - <,У
^"/оМ, ^+00^=0.
Решая характеристическое уравнение г: 'г- -5г - 4" •= ^> , получим: ii =<', ^ = -У . Тогда общее решение будет:
у^б^-к^е^ , у^ ^-^-е^- ^в^. Удовлетворяя краевым условиям:
( !/'(с)^ ^•0-е^й.е-0^
^-f^--^ ''/^ ^-г^-О^^о
[it-7 0й 1»-7ОТ
Второе условие выполняется только при С-/ ^ о . Тогда из первого условия получим <• •0 Q c>~ Сл--{ = ^ -т- <^-= - ^
•— Ti*
Итак решение задачи будет: у = - ^ е (рис.5).
Рис.5
| при |
Ш. Решить дифференциальное уравнение: у ~У0 граничных условиях: С и Со) ^ 5
ti^)-yY^r
Общее решение будет Краевые условия дают:
fc<^e»=3
\С^ Oe'-^e^/
Решение будет ^^ f-f- He - единственное решение. Очевидно, для решения краевой задачи основной трудностью является нахождение общего решения дифференциального уравнения. Поэтому рассмотрим приближенные методы решений.
Похожие работы
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
0 комментариев