I (ol-i-x)c 6+Х-}
Экстремальные задачи в неполной средней школе
Л. Транспортная задача линейного программирования
Задача о рационе
Понятие о задаче нелинейного программирования
Понятие о краевых задачах
Приближенный метод решения краевых задач. Конечно-разностный алгоритм
Постановка простейшей задачи
Метод Эйлера в вариационной задаче
Алгоритм решения линейной вариационной задачи
Об одном подходе к решению нелинейных вариационных задач
Навигация
Метод Эйлера в вариационной задаче
К решению нелинейных вариационных задач
57698
знаков
75
таблиц
8
изображений
3.2. Метод Эйлера в вариационной задаче
Основоположником конечно-разностного метода в вариационном исчислении является Леонард Эйлер. Однако, в связи с громоздкими вычислениями, которые требует данный метод, до изобретения ЭВМ он не получил широкого применения. Лишь компьютерная революция в математике способствовала широкому внедрению метода Эйлера, и в настоящее время разные модификации его получили распространение в прикладной математике.
Пусть дана простейшая вариационная задача: найти экстремум функционала ^
| (1) |
^£^)] - jf f^y,^)^
yf^)-^. ^/(^)-у^.
т.е. здесь надо найти такую кривую у С^) -, чтобы
^п: ^Г^;7= yCyW3 .
По методу Эйлера разобьем интервал Гль^З на П. частей точками (см.рис. II): , ^ з^-^ Л^^ ЛЬ-^^ , ^= <2,..., гъ ^ h- ~ ^
Необходимо найти ординаты у/,.. -, 4)- < соответствующие точкам х'/ i' /
--"-/, .,. , J^.n.-< •
Таким образом, искомую' функцию ^(^-} ищем в табличной форме:
| ое | До | ^ | 1 | '-<?«.- -f | У <--<,ц, |
| ^ | ^ | ^ | 1 ' 1 | ^ | ^ |
uf^\~ ^l(^)-^) ^^^
У 1/ ——И——— " ~И—— '
| (2) |
интеграл (1) заменим суммой:
Зчт. п-f
^1^']р(^')^^Г(л^, ^^).L --
— лл t ^ J J
- Ф^-^-J
40
Ординаты У/, ..., j//i-/ выбирают так, чтобы функция 9? (у^ •, ^-/ У достигла экстремума ( как функция л---/ переменных У-/,-•• ^-•r ), т.е. находятся из условия:
| 9(р - о - ' ^^ - О . ^ ' •" ; ^ "" |
б)^
^0 ;
| (3) |
/ ^Р ( Ъ^
| В целях достижения достаточной точности число /I | берут до- | ||||||||
| вольно большим. При этом приходится решать систему типа | (3)с n-f | ||||||||
| неизвестными, т.е. высокого порядка. | |||||||||
| ^ | |||||||||
| •i1 | \ | ||||||||
| ^ | .'^/ | ||||||||
| Ч-- | 'л | г г - | ^- | I/t• | |||||
| -X'o 3-i ЗСд, Эе,- Jc't'+i' ^ , Рис. 11 | Гк Я1. | ||||||||
Пример. Найти приближенное решение задачи о минимуме функционала ^
^J-J^+^b^^e, ^(oY--^^)--O
0 f /,<9 Решение. Возьмем Л = ~~s~ ^ °/^ и положим
^-^о)-0 ; ^^(^2); ^-^(О^),
^-^°^ ^--Ц1°^^ ^-:^~-0• Значения производных приближенно заменим по формуле
^•-^'(v^)к ^^ ^-
Тогда
41
| ^-^ о.г |
t/ у/п /'} - ^-^
| ; У^б |
; ^^Л -^2-
,7 - I -/ - ^ . ^ ^ Данный интеграл заменяем суммой по формуле прямоугольников
"S-f^d^ ^ с ^o.}+^)^^^^)']-k
| Будем иметь а- |
| Будем иметь а' щ-w'.) <^-/^ (о^ ^•°)^ (W^y^- ^ -. (^)^^S.^ . (^L)^^ ^-^ ^ |
| (W^^^^-0^ |
Будем иметь а-
-+
Составляем систему уравнений для определения ^ ^ ^ /Л, искомой ломаной:
^н^' 2(^'OJ•/ ^ -^^^^"^^'^^ ^^0
^ '-[(^•д ^^/+^•г^^X^+ ^.г.^ •^ -о •^гГ^•г^-^/+^^-м^+^^'^L7г=o. ^-f^'^-^-^^'^^^'^^ ^
<7 \ у ( ^л^. и^л- •9^-^---^
| или |
^^^^ "-^ -=~^о^ ^ -Ь ^,00^^ - ^ = -0,0^
- ^ -+ ^^ -^ , .о^
-^ + S,00i{^ = - ^0^!L ^
у^^^т; ^--^w; у^о^^^. ^ о,^ш.
___т.е.________________________________________
| Х | о | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| ^ | о | 0,132 | 0,273 | 0,402 | 0,522 | 0 |
| 7 |
Точное решение исходной задачи:
^TS^^; ^~ (^ ~c' ~ ^"-у^-^
Тогда решение краевой задачи
/Sri%- ^f0^^ ^^0
42
будет: u(r)^(eл-ix)-e/(^-ei)+x.^-q^6sя.(e!^e^)•^
Приведем сравнительную таблицу:'
| У | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| ^ | 0 | 0,13712 | 0,27341 | 0,40211 | 0,52231 | 0 |
| ^- | о | 0,13693 | 0,27142 | 0,40071 | 0,52199 | 0 |
Таким образом метод Эйлера дает весьма удовлетворительные результаты в смысле точности.
Рассмотрим случай п. ~? оо в методе Эйлера.
Из(2)имеем: ф (^„...,у^) ^- { F ^-^ЗД +." + +F (Г^, ^, ^^^F(^,y., ^-)^„^^(Х^,^,
^^%}]. Тогда система (3) для определения ^ , ^ , ..., i/^-f будет:
1^^^ k-[0^^o^F^-^ ^^, +Fy^(~/^io^o
-^-^/^^^J-^^^^-^J;//^
Переходя к пределу при /l-> po , получим уравнение Эйлера
которому должна удовлетворять искомая функция у/х.), реализующая экстремум. Аналогично может быть получено основное необходимое условие экстремума в других вариационных задачах.
43
Похожие работы
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
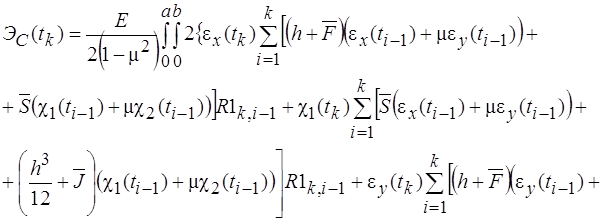
0 комментариев