I (ol-i-x)c 6+Х-}
Экстремальные задачи в неполной средней школе
Л. Транспортная задача линейного программирования
Задача о рационе
Понятие о задаче нелинейного программирования
Понятие о краевых задачах
Приближенный метод решения краевых задач. Конечно-разностный алгоритм
Постановка простейшей задачи
Метод Эйлера в вариационной задаче
Алгоритм решения линейной вариационной задачи
Об одном подходе к решению нелинейных вариационных задач
Навигация
Л. Транспортная задача линейного программирования
К решению нелинейных вариационных задач
57698
знаков
75
таблиц
8
изображений
1.7 Л. Транспортная задача линейного программирования
1. Постановка задачи : Пусть на двух станциях ^4 и /\, сосредоточено
соответственно Ct, и 0.^ тонн груза, который необходимо доставить в пункты 6 , Ь-г., В,, в количестве I,, ^д , ^ , соответственно. Стоимость перевозки 1
тонны груза со станции у1, в пункты В,, Вд, &з составляет Сц , С^, G^ рублей
соответственно. Аналогично - стоимость перевозки со станции Л>в пункты В/, bj, б»з составляет G, , С^ ,Сщ рублей. Требуется организовать перевозку так,
чтобы общая стоимость этой перевозки была наименьшей. Все данные
представим в виде таблицы 1.
| ^^ /•"^ | В/ | fi. | ^ | Кол-во отправленного | ||
| t ^^^ | груза | |||||
| е^ | (^ | (^ | ||||
| А, | ^ | ^2 | ^3 | й< | ||
| Сг/ | С?? | Сгз | ||||
| А. | х„ | ^2 | •Ггз | ft, | ||
| Кол-во доставленного | &< | ^ | ^ | |||
| груза | ||||||
Таблица 1
20
Математическая модель задачи
Обозначим через -^-количество груза, перевозимого со станции aj в пункт 6^ . Тогда общая стоимость перевозки будет + При этом Jl^t .?. о и удовлетворяет условиям:
|
|
^ с/, х„ ^ е^ ^ ^... ^ ^з -г^ - и и е^; (<) ^ с^ ^/
'S ^ ^CU Г ^ ^ ^ ^ •2?<5 = Ог
^ т.ч. \ ^-f-Xss. -f-^.^CLi . ^-- ^ \ ^^Х,, =^ (2)
Л/2 + ^22 = Ьг
^ Зеез, ^ Д-^з = &
Итак: найти неотрицательное решение системы уравнений (2) дающее минимальное значение линейной формы (1).
Решение задачи (частный случай) Пусть 0{ -- 200, Лг. = /60 ^ ^ = f^O , & = 90, ^ = W,
Сн - б , С ^ = ^ С^ = 2 , С,, = S, С^ - J, ^з -= 2.
Для удобства обозначим -IV/ =:с » -^/'a :=t/ . Тогда из (2) и условия задачи получаем следующую систему неравенств:
Г X г0, У 7^0 , Х,л ^CL-( Х„ + Х^ ) = & - (^-+У) ^0 ' .У^^-ге^, Хаг ^&-^?^,
^2.^^^^/-^^)= ^2-^-&^ (^.^^>
В нашем случае оно примет вид:
' З^У.О^г.О Г О ^ эеf^ ^0
^у^2^ ^ ^^у^^ ^/;
^^^0,^^90 ] / JC^y^-У^ 1^^ ^^^У^^6?0
Тогда: -^ S^-h^^f-h 2- lsoo- (y^J -^S L W- X. J + + 3 ^^-^ + ^ L~ Юч- зе^З ш^ А зе^У + ^30 U f)
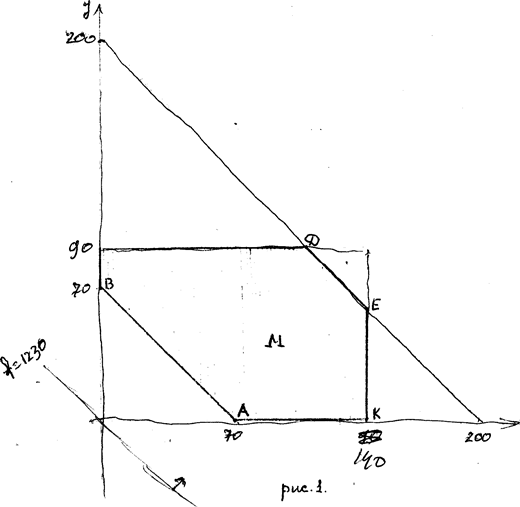
i Решение системы неравенств (2 ) будет выпуклое ограниченное
множество М. Рис. 1, а линейная форма т= х^У ^230 принимает при этом минимальное значение на стороне C^6J множества J4., т.е. на прямой
"я^^ЧО Здесь решение задачи есть множество точек отрезка прямой Г^З . Итак, мы можем взять любую точку на прямой х+-У= Ю . Возьмем, например, точку A (f0',o) , т.е. 'JC-^OC^ Ю, У^О . Тогда
а?/з = ^0 , Хц ^ f0 , Лгг ^ 90, Х^ъ =0.
21
При этих значениях таблица 1 - принимает вид:
| ^^ь. ,4;-^ | &г | В. | Вз | Кол-во отправленного груза |
| А, | Ю | о | f30 | ^00 |
| Аг | 40 | 90 | о | /60 |
| Кол-во поставленного груза | 1^0 | 90 | /зо |
| При такой схеме перевозок затраты на них будут наименьшими и равны 1300. |
22
Похожие работы
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
... в руки инженера эффективную вычислительную процедуру решения задачи оптимизации управления, хорошо приспособленную к использованию ЭВМ. Этот метод мы рассмотрим более подробно. 2.4. Метод динамического программирования 2.4.1. Дискретная форма вариационной задачи Преодоление рассмотренных трудностей решения вариационной задачи лежит на путях использования эффективных вычислительных методов ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... задачи динамики, определять, при каких условиях осуществимо движение с заданными свойствами. С другой стороны, и само развитие теории управления движениями материальных систем вызвало необходимость решения обратных задач динамики в различных постановках. Все это привело к тому, что обратные задачи классической механики оказались своего рода направляющими и исходными задачами современной науки об ...
0 комментариев