Навигация
2. Экстремумы
Точка
![]() называется
точкой локального
максимума
(минимума)
функции
называется
точкой локального
максимума
(минимума)
функции ![]() ,
если для всех
точек
,
если для всех
точек ![]() (
(![]() )
из некоторой
окрестности
этой точки
справедливо
неравенство
)
из некоторой
окрестности
этой точки
справедливо
неравенство
![]() (
(![]() ).
Точки локального
максимума и
минимума называются
точками экстремума
функции.
).
Точки локального
максимума и
минимума называются
точками экстремума
функции.
Пример. В экономическом анализе применяется функция прибыли
![]() ,
,
где ![]() – производственная
функция,
– производственная
функция, ![]() – цена выпускаемой
продукции,
– цена выпускаемой
продукции, ![]() и
и ![]() – факторные
цены. Пара чисел
(
– факторные
цены. Пара чисел
(![]() )
называется
оптимальным
планом, если
функция
)
называется
оптимальным
планом, если
функция ![]() достигает
максимума при
достигает
максимума при
![]() .
Таким образом,
поиск оптимального
плана сводится
к отысканию
точки экстремума
(максимума)
функции прибыли
.
Таким образом,
поиск оптимального
плана сводится
к отысканию
точки экстремума
(максимума)
функции прибыли
![]() .
.
Следующие теоремы позволяют находить точки экстремума функций.
Теорема (необходимое
условие экстремума).
Если функция
![]() имеет в точке
экстремума
имеет в точке
экстремума
![]() частные производные
первого порядка,
то они равны
нулю в этой
точке:
частные производные
первого порядка,
то они равны
нулю в этой
точке:
![]() . (1)
. (1)
Точки,
координаты
которых удовлетворяют
системе (1) называются
стационарными
точками функции
![]() .
Точки экстремума
функции следует
искать среди
ее стационарных
точек и тех
точек, в которых
частные производные
первого порядка
не существуют.
.
Точки экстремума
функции следует
искать среди
ее стационарных
точек и тех
точек, в которых
частные производные
первого порядка
не существуют.
Теорема (достаточное
условие экстремума).
Пусть функция
![]() имеет непрерывные
частные производные
второго порядка
в некоторой
окрестности
своей стационарной
точки
имеет непрерывные
частные производные
второго порядка
в некоторой
окрестности
своей стационарной
точки ![]() .
Положим
.
Положим
![]() .
.
Тогда:
а) если ![]() и
и ![]() ,
то
,
то ![]() - точка максимума
функции;
- точка максимума
функции;
б) если ![]() и
и ![]() ,
то
,
то ![]() - точка минимума
функции;
- точка минимума
функции;
в) если ![]() ,
то в точке
,
то в точке ![]() экстремума
нет.
экстремума
нет.
Пример.
Стационарная
точка ![]() ,
,
![]() функции
функции
![]()
является решением системы уравнений
![]() ,
,
![]() .
.
При этом
![]() ,
,
![]() ,
,
![]() и
и ![]() .
Следовательно,
в точке
.
Следовательно,
в точке ![]() функция имеет
локальный
минимум.
функция имеет
локальный
минимум.
Пример. Пусть
![]() .
Тогда
.
Тогда ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
и, следовательно,
стационарная
точка
,
и, следовательно,
стационарная
точка ![]() не является
точкой экстремума.
не является
точкой экстремума.
Пример. Для
функции ![]() из системы
уравнений
из системы
уравнений
![]() ,
, ![]() ,
,
найдем
четыре стационарные
точки: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Поскольку
.
Поскольку ![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
В точках
![]() и
и ![]() выполнено
условие
выполнено
условие ![]() ,
поэтому функция
имеет экстремумы
в этих точках:
минимум в
,
поэтому функция
имеет экстремумы
в этих точках:
минимум в ![]() ,
так как
,
так как ![]() ,
и максимум в
,
и максимум в
![]() ,
так как
,
так как ![]() .
В точках
.
В точках ![]() и
и ![]() экстремумов
нет, так как
экстремумов
нет, так как ![]() в этих точках.
в этих точках.
Упражнения
1. Найти частные производные первого порядка следующих функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
2. Найти смешанные производные функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) 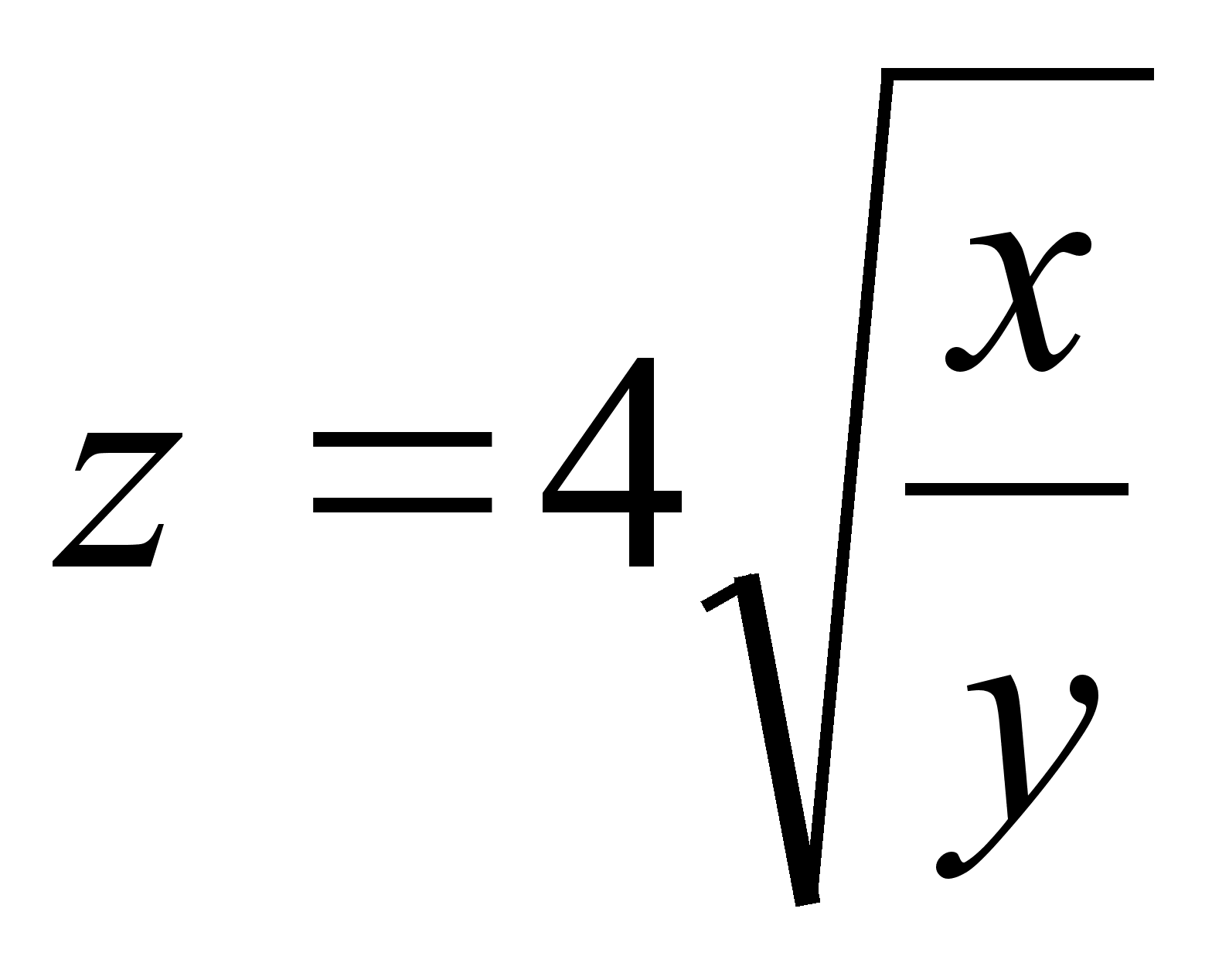 ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
3. Найти стационарные точки функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;.
;.
6) ![]() );
);
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
4. Найти точки локального экстремума функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
Ответы
1.
1) ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ;
;
4) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() ;
;
6) 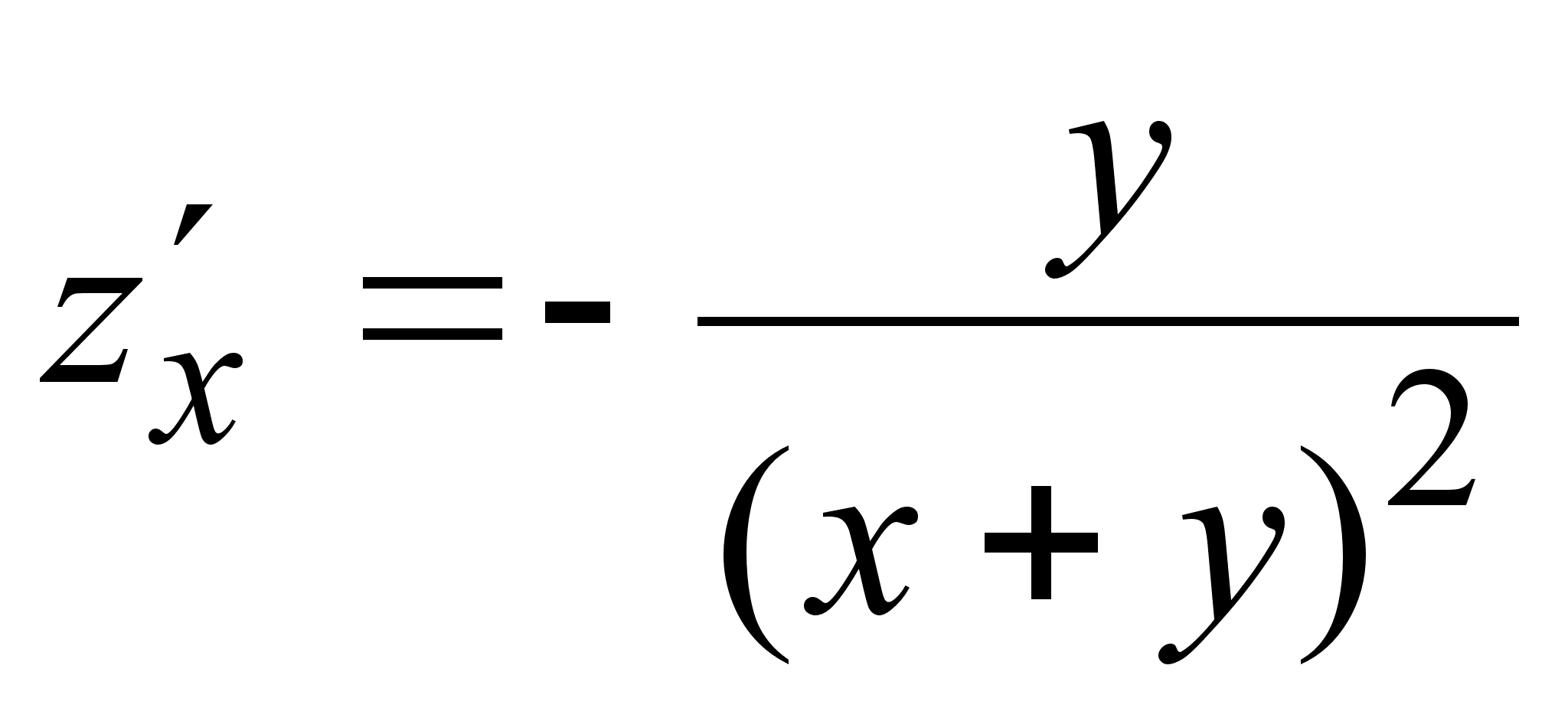 ,
, 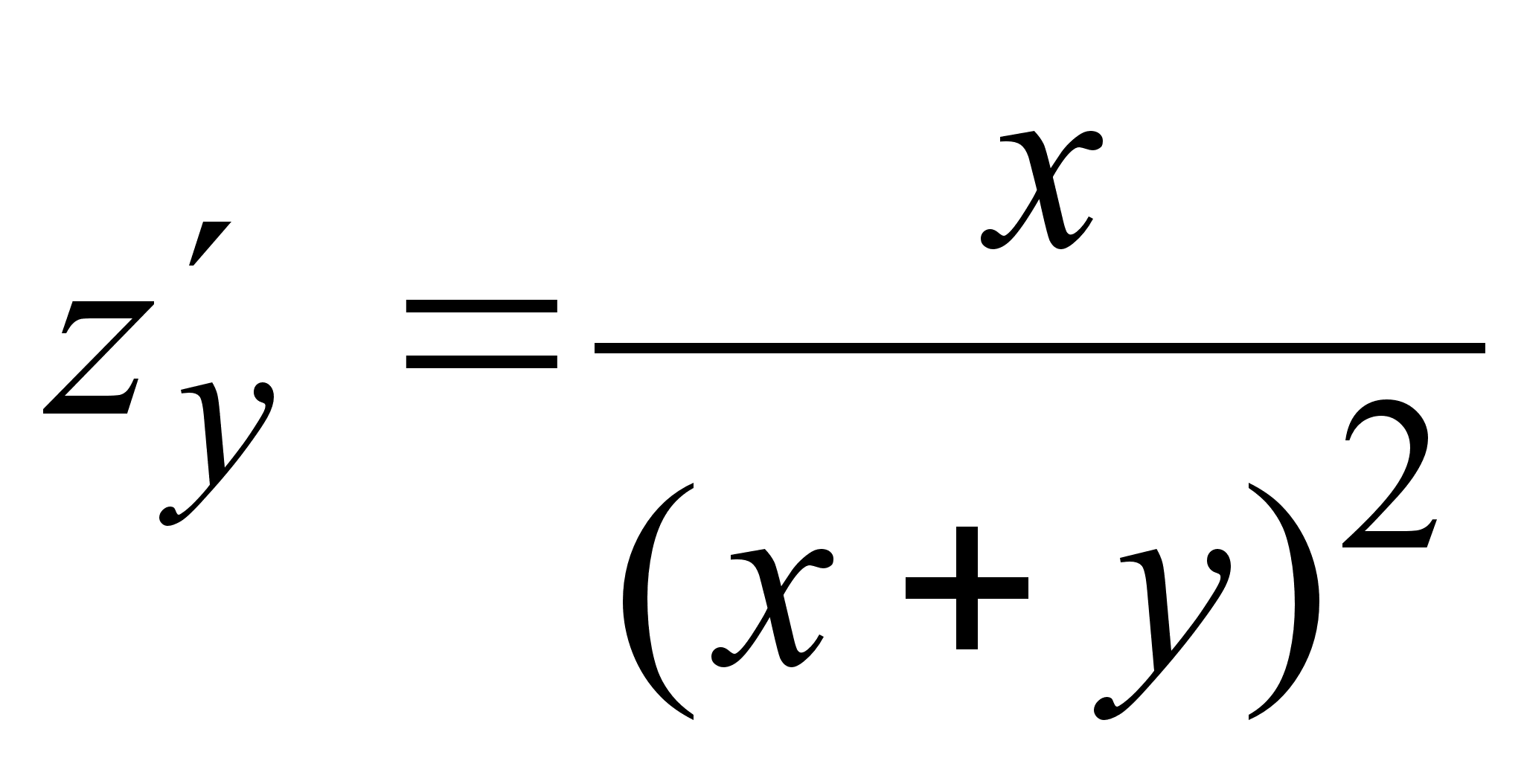 ;
;
7) ![]() ;
; ![]() ;
;
8) ![]() ,
, 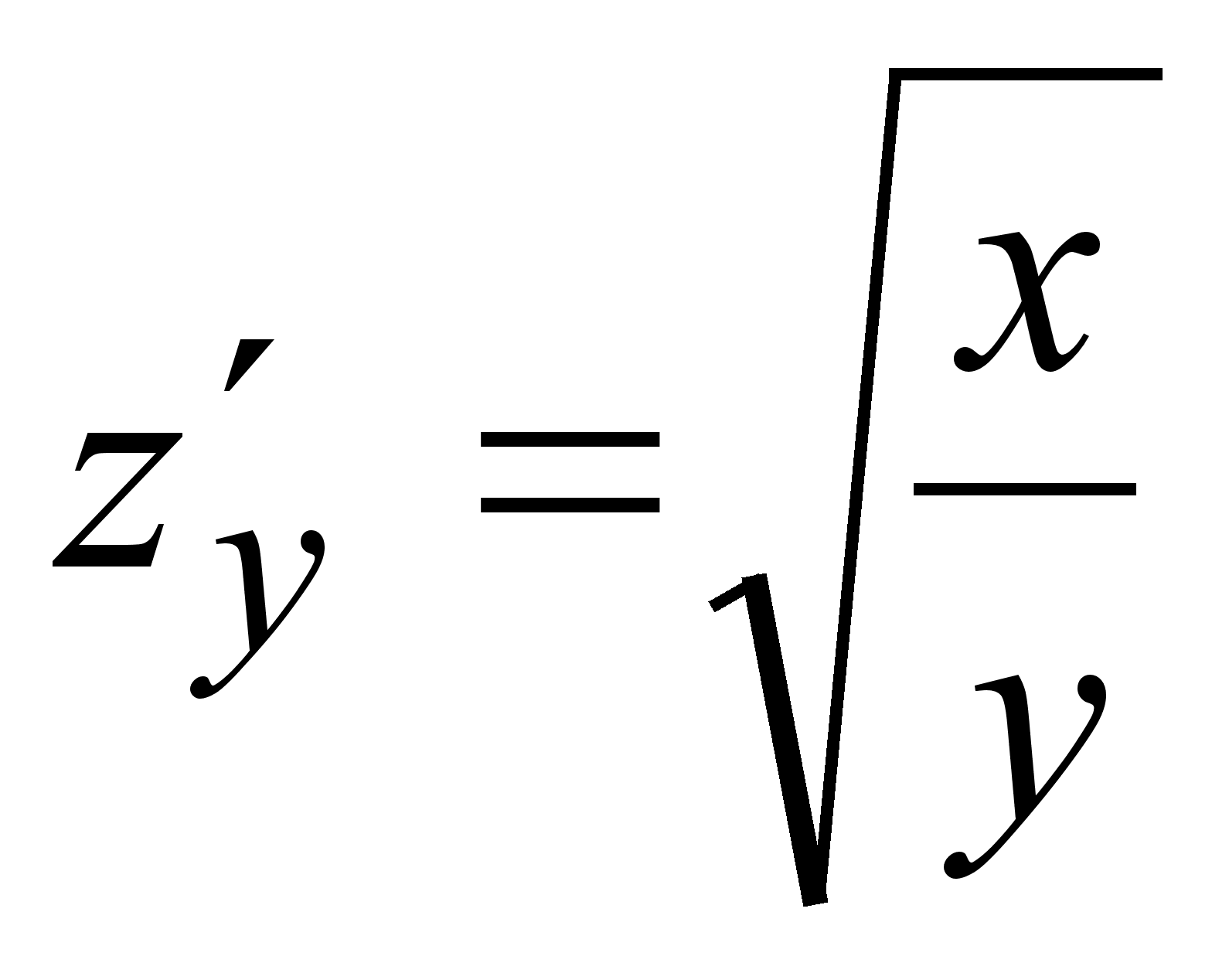 ;
;
9) ![]() ,
, ![]() ;
;
10) ![]() ,
, ![]() .
.
2.
1) 0;
2) ![]() ;
;
3) ![]() ;
;
4) 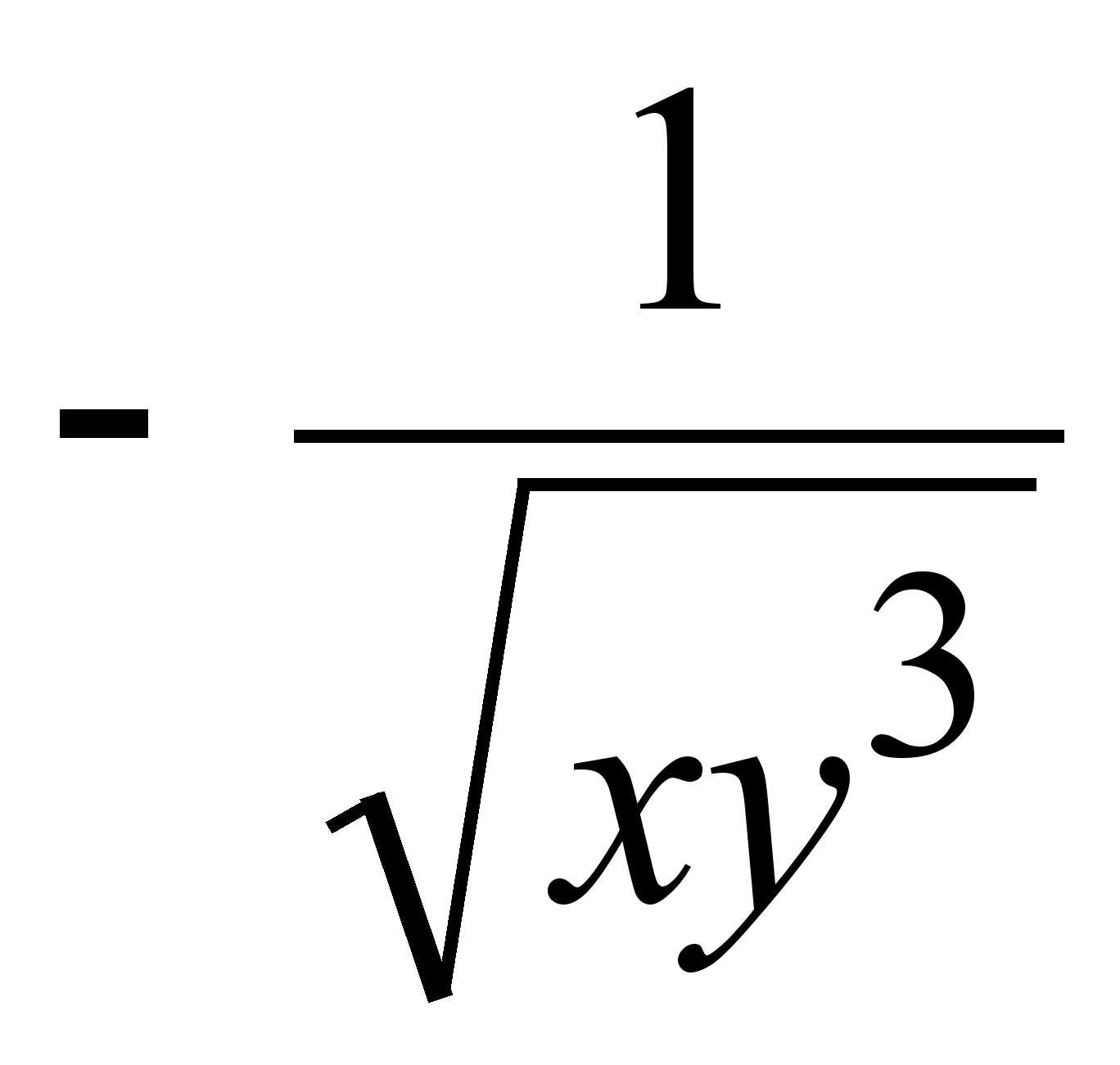 ;
;
5) 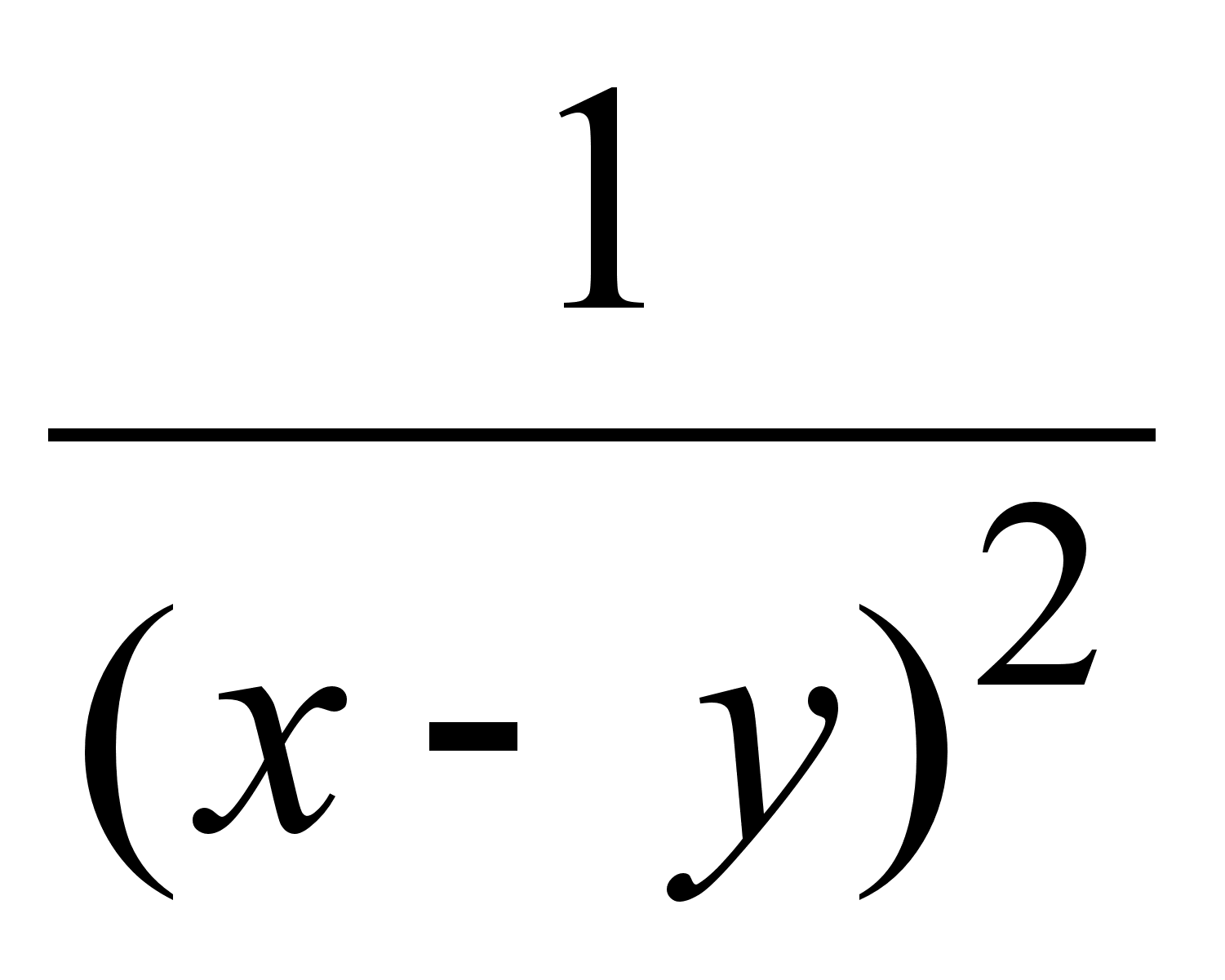 ;
;
6) 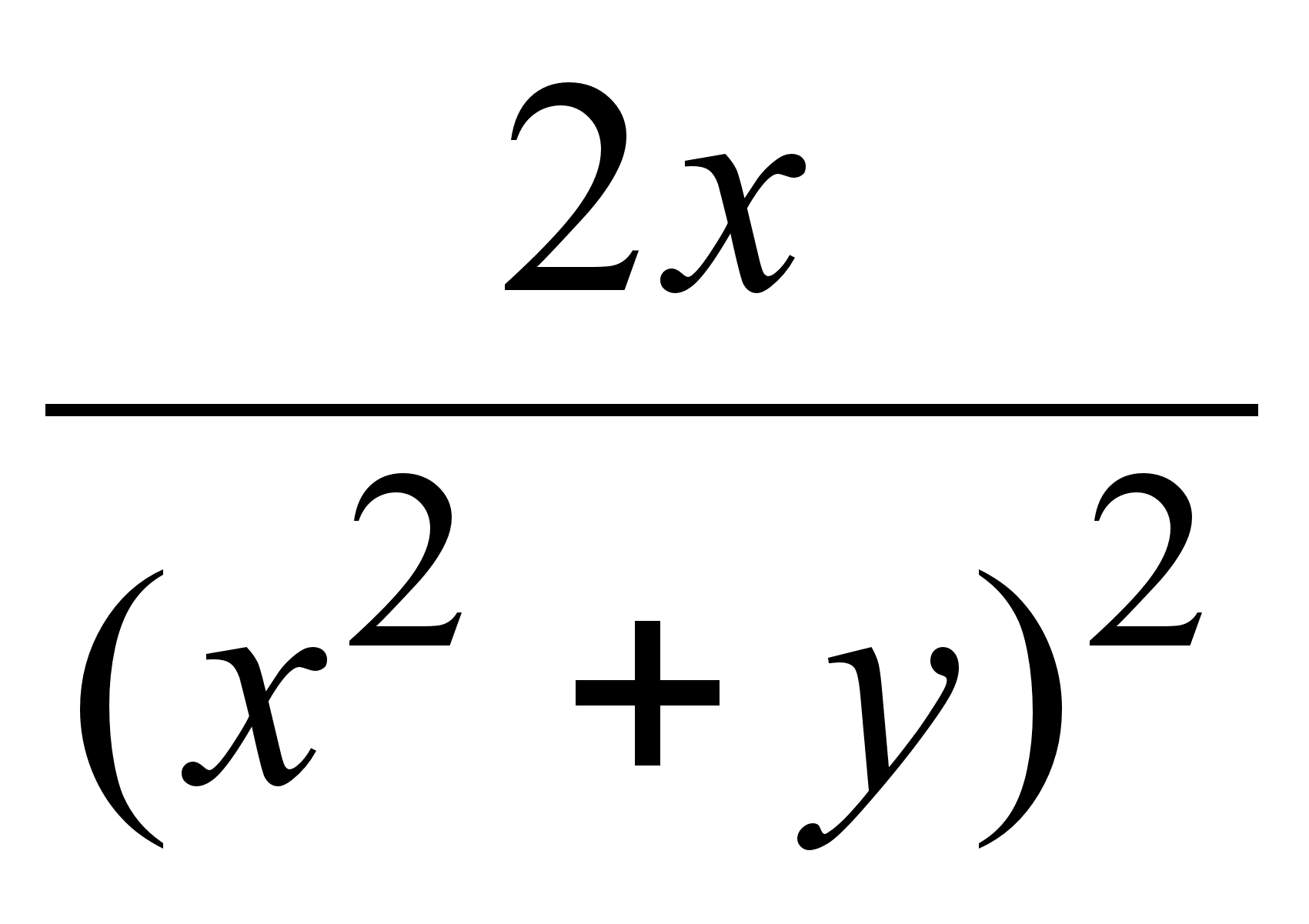 ;
;
7) 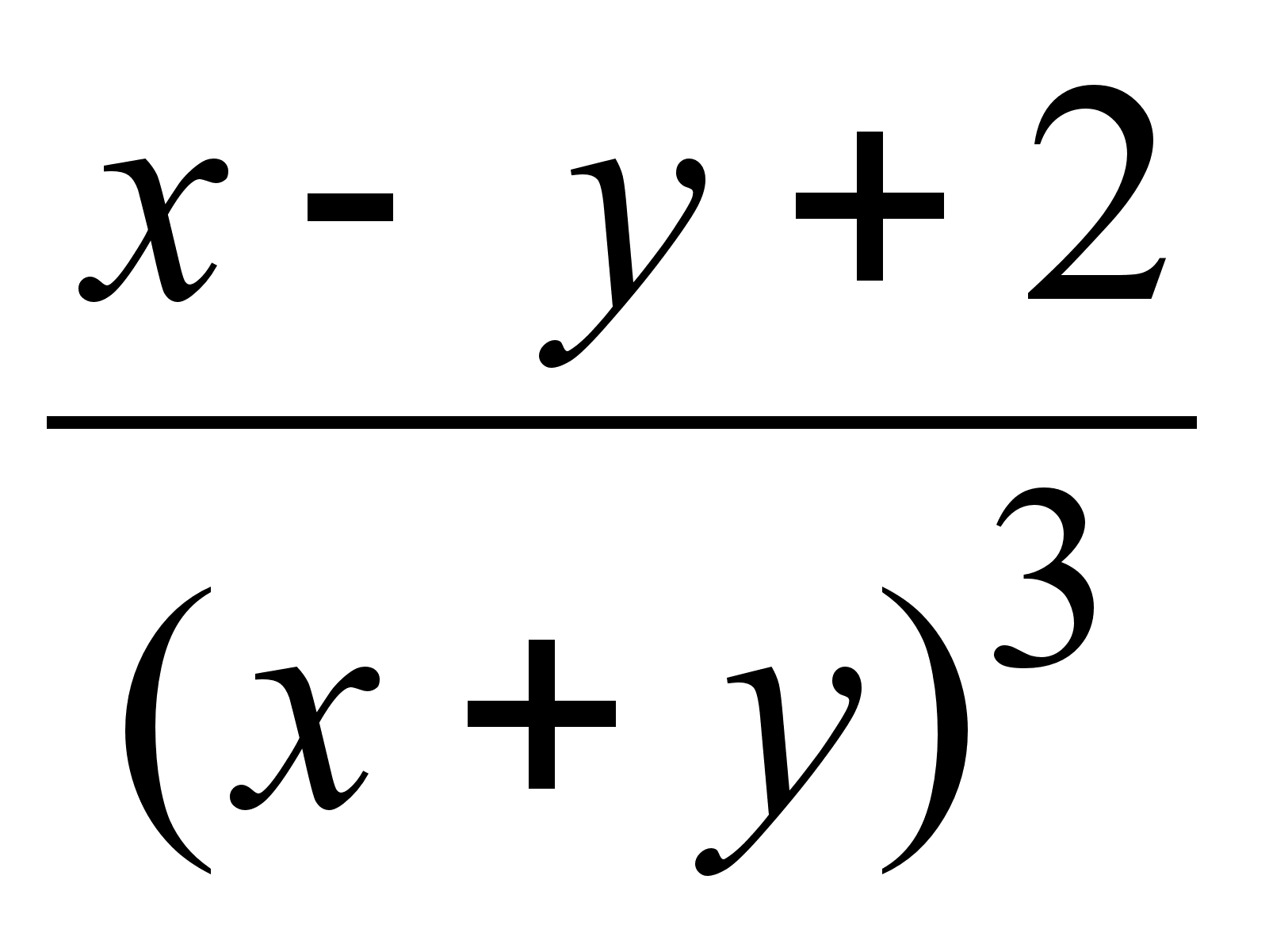 ;
;
8) 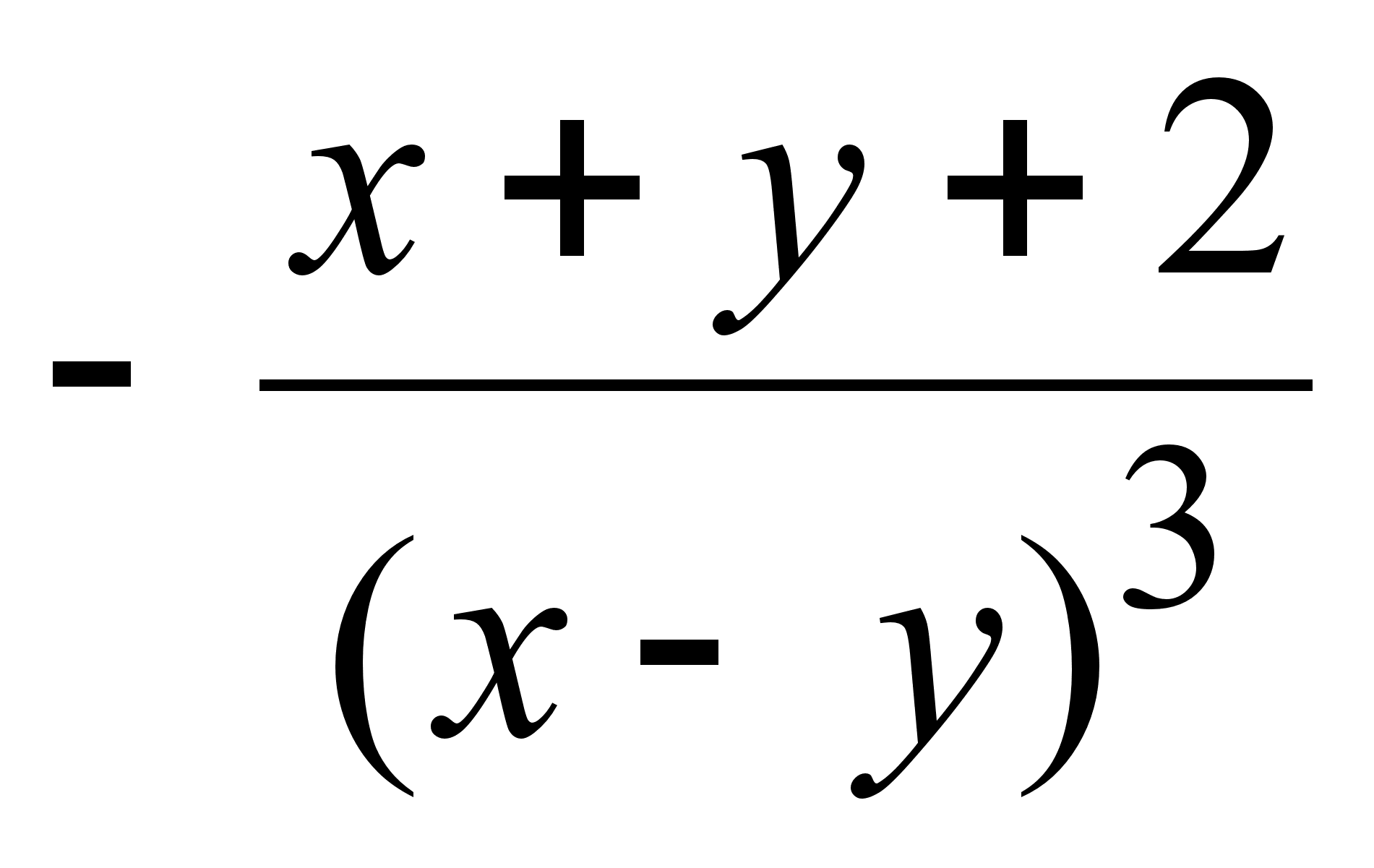 ;
;
9) ![]() ;
;
10) ![]() .
.
3.
1) (0,1);
2) ![]() ;
;
3) (1,2);
4) ![]() ;
;
5) ![]() и
и ![]() ;
;
6) стационарных точек нет;
7) ![]() ;
;
8) ![]() ;
;
9) стационарных точек нет;
10) ![]() .
.
4.
1) ![]() - точка минимума;
- точка минимума;
2) ![]() - точка минимума;
- точка минимума;
3) ![]() - точка максимума;
- точка максимума;
4) и 5) функция не имеет точек экстремума;
6) ![]() - точка минимума;
- точка минимума;
7) ![]() - точка минимума;
- точка минимума;
8) ![]() - точка максимума;
- точка максимума;
9) функция не имеет точек экстремума;
10) ![]() - точка минимума;
- точка минимума; ![]() - точка максимума.
- точка максимума.
§ 7. Обыкновенные дифференциальные уравнения
Математическое исследование многих реальных процессов основано на применении дифференциальных уравнений, содержащих производные искомых функций. Аппарат дифференциальных уравнений универсален: разнообразные процессы могут описываться одинаковыми уравнениями. Практика показывает, что даже простые математические модели, использующие дифференциальные уравнения, позволяют качественно изучить основные черты сложных явлений и оценить их количественные характеристики.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
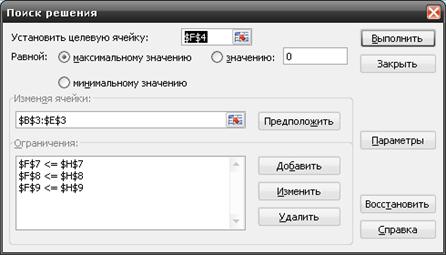
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





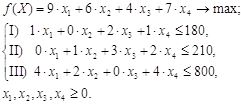
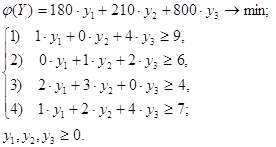
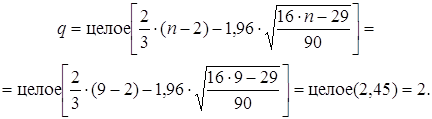
0 комментариев