Навигация
1. Определения
Пусть каждой
точке ![]() некоторого
множества
некоторого
множества ![]() плоскости
поставлено
в соответствие
число
плоскости
поставлено
в соответствие
число ![]() ,
тогда говорят,
что на множестве
,
тогда говорят,
что на множестве
![]() задана функция
двух переменных
задана функция
двух переменных ![]() .
Используется
также запись
.
Используется
также запись
![]() .
.
Пример. В экономических приложениях встречаются производственные функции, устанавливающие связь между затратами производственных ресурсов и объемом выпускаемой продукции. Производственные функции, как правило, зависят от многих переменных (факторов). В частности, рассматриваются двухфакторные функции
![]() ,
,
где ![]() - объем производственных
фондов,
- объем производственных
фондов, ![]() -
затраты труда,
-
затраты труда,
![]() -
объем выпускаемой
продукции.
Примером
двухфакторной
функции является
функция Кобба-Дугласа
-
объем выпускаемой
продукции.
Примером
двухфакторной
функции является
функция Кобба-Дугласа
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() - постоянные.
- постоянные.
Окрестностью
точки ![]() назовем внутренность
любого круга
с центром в
этой точке.
Пусть функция
назовем внутренность
любого круга
с центром в
этой точке.
Пусть функция
![]() определена
в некоторой
окрестности
точки
определена
в некоторой
окрестности
точки ![]() .
Зафиксируем
значение
.
Зафиксируем
значение ![]() и рассмотрим
функцию
и рассмотрим
функцию ![]() одной переменной
одной переменной
![]() .
Производная
функции
.
Производная
функции ![]() в точке
в точке ![]() (если она существует)
называется
частной производной
функции
(если она существует)
называется
частной производной
функции ![]() в точке
в точке ![]() по переменной
по переменной
![]() и обозначается
и обозначается
![]() .
Аналогично
определяется
частная производная
.
Аналогично
определяется
частная производная
![]() по переменной
по переменной
![]() .
.
Производные
![]() и
и ![]() функции
функции ![]() называются
частными производными
первого порядка.
Если они существуют
в некоторой
окрестности
точки
называются
частными производными
первого порядка.
Если они существуют
в некоторой
окрестности
точки ![]() ,
то частные
производные
от них по
,
то частные
производные
от них по ![]() и
и ![]() называются
частными
производными
второго порядка
и обозначаются
называются
частными
производными
второго порядка
и обозначаются
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где, например,
,
где, например,
![]() ,
,
![]() .
Производные
.
Производные
![]() ,
,
![]() называются
смешанными
частными
производными.
называются
смешанными
частными
производными.
Аналогично можно ввести частные производные третьего и более высоких порядков. Из определения частных производных следует, что для их нахождения можно использовать все правила, справедливые для производных функций одной переменной.
Примеры. Найдем частные производные первого и второго порядков функций:
а)
![]() ,
тогда
,
тогда
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Равенство смешанных производных, наблюдаемое в приведенных примерах, не случайно. Справедливо следующее общее утверждение.
Теорема. Если
производные
![]() ,
,
![]() существуют
в некоторой
окрестности
точки
существуют
в некоторой
окрестности
точки ![]() и непрерывны
в этой точке,
то справедливо
равенство
и непрерывны
в этой точке,
то справедливо
равенство
![]() .
.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
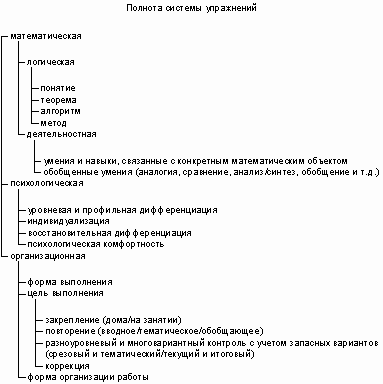
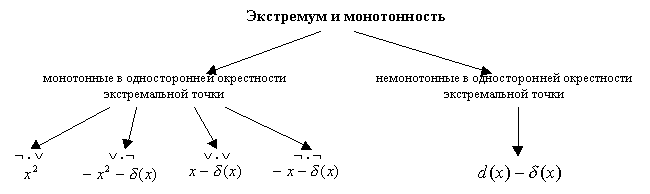
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
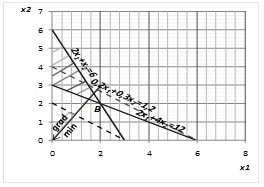
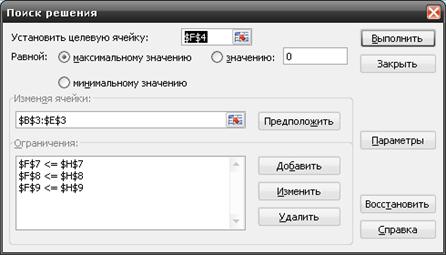
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





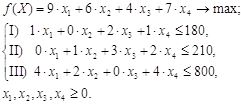
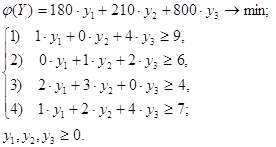
0 комментариев