Навигация
4. Эластичность функции
![]()
Пусть аргумент ![]() функции
функции ![]() получает приращение
получает приращение ![]() . Тогда значение функции изменяется на величину
. Тогда значение функции изменяется на величину ![]() . Отношение
. Отношение ![]() характеризует среднее изменение функции, приходящееся на единицу изменения ее аргумента, а предел этого отношения при
характеризует среднее изменение функции, приходящееся на единицу изменения ее аргумента, а предел этого отношения при ![]() равен производной
равен производной ![]() .
.
Рассмотрим относительные изменения переменных ![]() и
и ![]() , выраженные, например, в процентах:
, выраженные, например, в процентах: ![]() и
и ![]() . Их отношение
. Их отношение
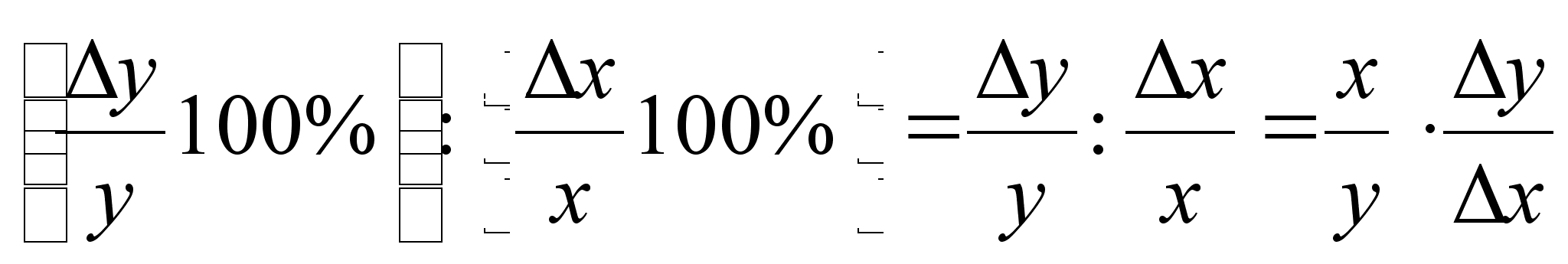
показывает, на сколько процентов в среднем меняется ![]() при изменении
при изменении ![]() на
на ![]() . Предел этого отношения при
. Предел этого отношения при ![]() называется эластичностью функции
называется эластичностью функции ![]() и обозначается
и обозначается ![]() , то есть
, то есть
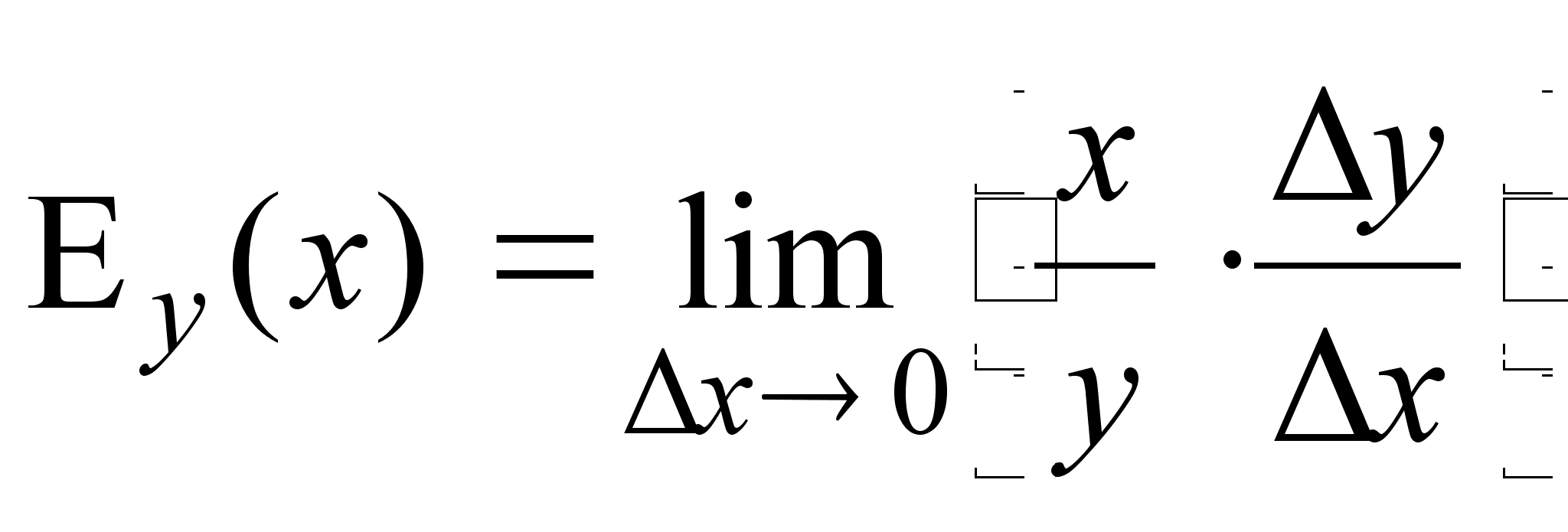 .
.
Так как
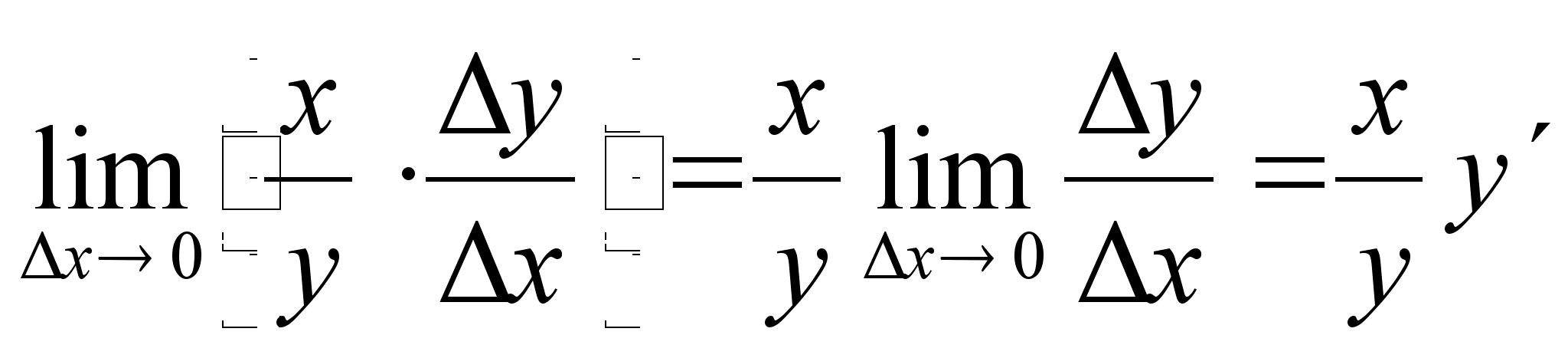 ,
,
то справедлива формула
![]() .
.
Примеры. а) Пусть ![]() , тогда
, тогда ![]() и, следовательно,
и, следовательно, ![]() . При
. При ![]() получаем
получаем ![]() , то есть при увеличении
, то есть при увеличении ![]() от 2 до 2,02 (на 1%) значение
от 2 до 2,02 (на 1%) значение ![]() изменяется примерно на
изменяется примерно на ![]() .
.
б) Пусть ![]() , тогда
, тогда ![]() и, следовательно,
и, следовательно, ![]() . При
. При ![]() получим
получим ![]() . Следовательно, увеличение
. Следовательно, увеличение ![]() от 3 до 3,03 ведет к уменьшению
от 3 до 3,03 ведет к уменьшению ![]() примерно на
примерно на ![]() .
.
в) Пусть ![]() , тогда
, тогда ![]() и, следовательно,
и, следовательно, ![]() . В этом случае эластичность постоянна и равна
. В этом случае эластичность постоянна и равна ![]() , то есть при любом значении аргумента его увеличение на 1% ведет к уменьшению значения функции также на
, то есть при любом значении аргумента его увеличение на 1% ведет к уменьшению значения функции также на ![]() .
.
Функция ![]() называется эластичной в точке
называется эластичной в точке ![]() , если
, если ![]() , нейтральной, если
, нейтральной, если ![]() , и неэластичной, если
, и неэластичной, если ![]() .
.
Пример. Дана зависимость спроса ![]() от цены
от цены ![]() :
:
![]() .
.
Найдем эластичность спроса ![]() , и рассмотрим ее значения при некоторых
, и рассмотрим ее значения при некоторых ![]() . Так как
. Так как ![]() , то
, то ![]() . При
. При ![]() имеем
имеем ![]() , откуда
, откуда ![]() , то есть спрос неэластичен. Если
, то есть спрос неэластичен. Если ![]() , то
, то ![]() ,
, ![]() , – спрос нейтрален. При
, – спрос нейтрален. При ![]() получим
получим ![]() , то есть
, то есть ![]() и, значит, спрос эластичен.
и, значит, спрос эластичен.
Эластичность спроса означает, что его относительное изменение по абсолютной величине превосходит относительное изменение цены; неэластичность означает меньшее относительное изменение спроса по сравнению с ценой; нейтральность – равенство этих изменений по абсолютной величине.
Пример. Пусть зависимость спроса от цены представлена функцией ![]() . Величина
. Величина
![]()
равна выручке, получаемой от продажи товара в объеме, равном спросу на товар. Выясним, как изменяется спрос с увеличением цены. Для этого найдем производную ![]() :
:
![]() ,
,
откуда
![]() .
.
Будем предполагать, что ![]() , поскольку, как правило, спрос уменьшается с ростом цены. В этом случае
, поскольку, как правило, спрос уменьшается с ростом цены. В этом случае ![]() и, следовательно, имеем
и, следовательно, имеем
![]() .
.
Отсюда видно, что если спрос эластичен (![]() ), то
), то ![]() , и с повышением цены выручка от продажи товара снижается; если спрос нейтрален (
, и с повышением цены выручка от продажи товара снижается; если спрос нейтрален (![]() ), то
), то ![]() , и выручка мало зависит от изменения цены; если спрос неэластичен (
, и выручка мало зависит от изменения цены; если спрос неэластичен (![]() ), то
), то ![]() , и выручка увеличивается с ростом цены.
, и выручка увеличивается с ростом цены.
Упражнения
1. Найти производные ![]() функций:
функций:
1) ![]() ;
;
2)![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) 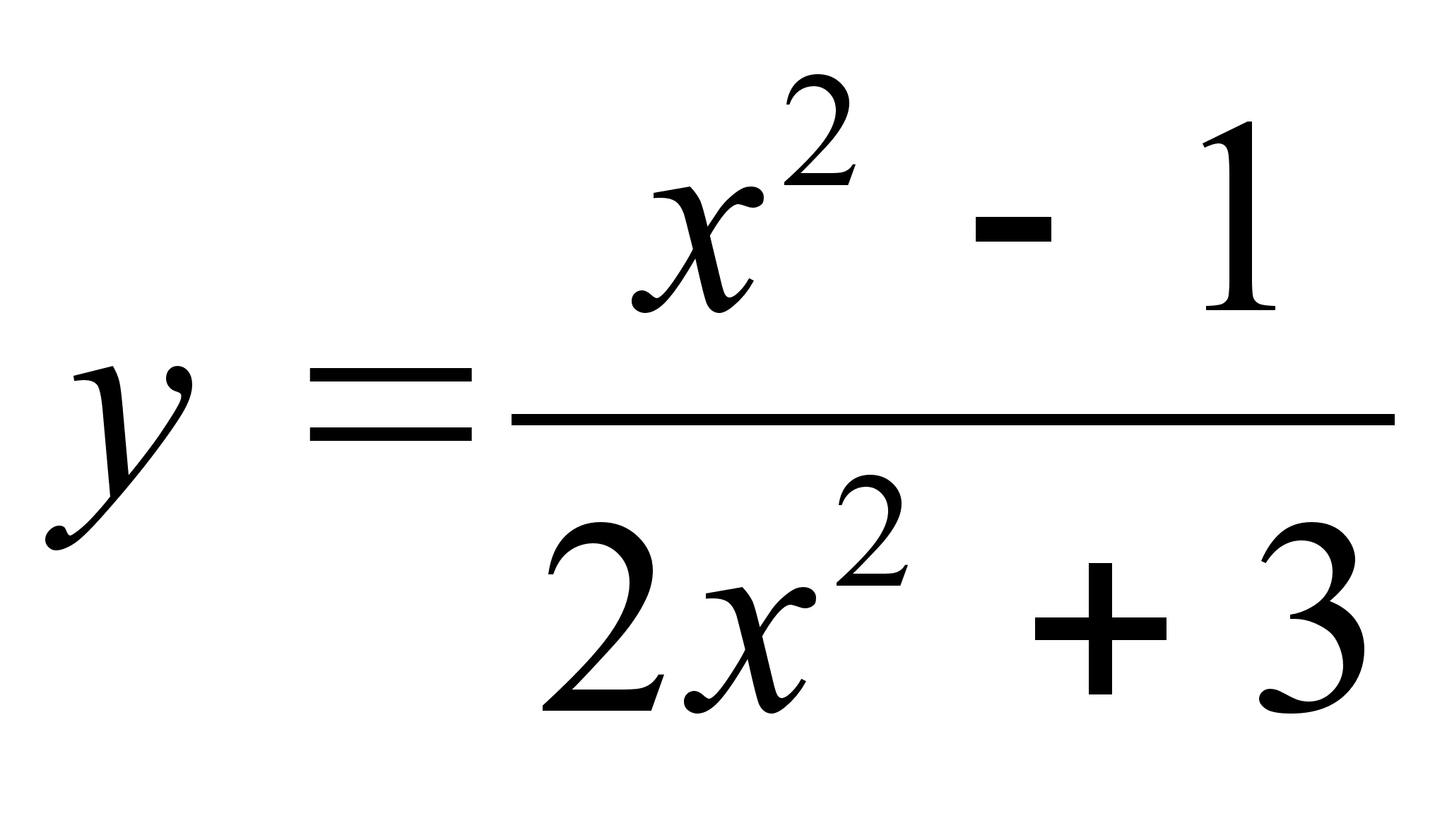 ;
;
13) 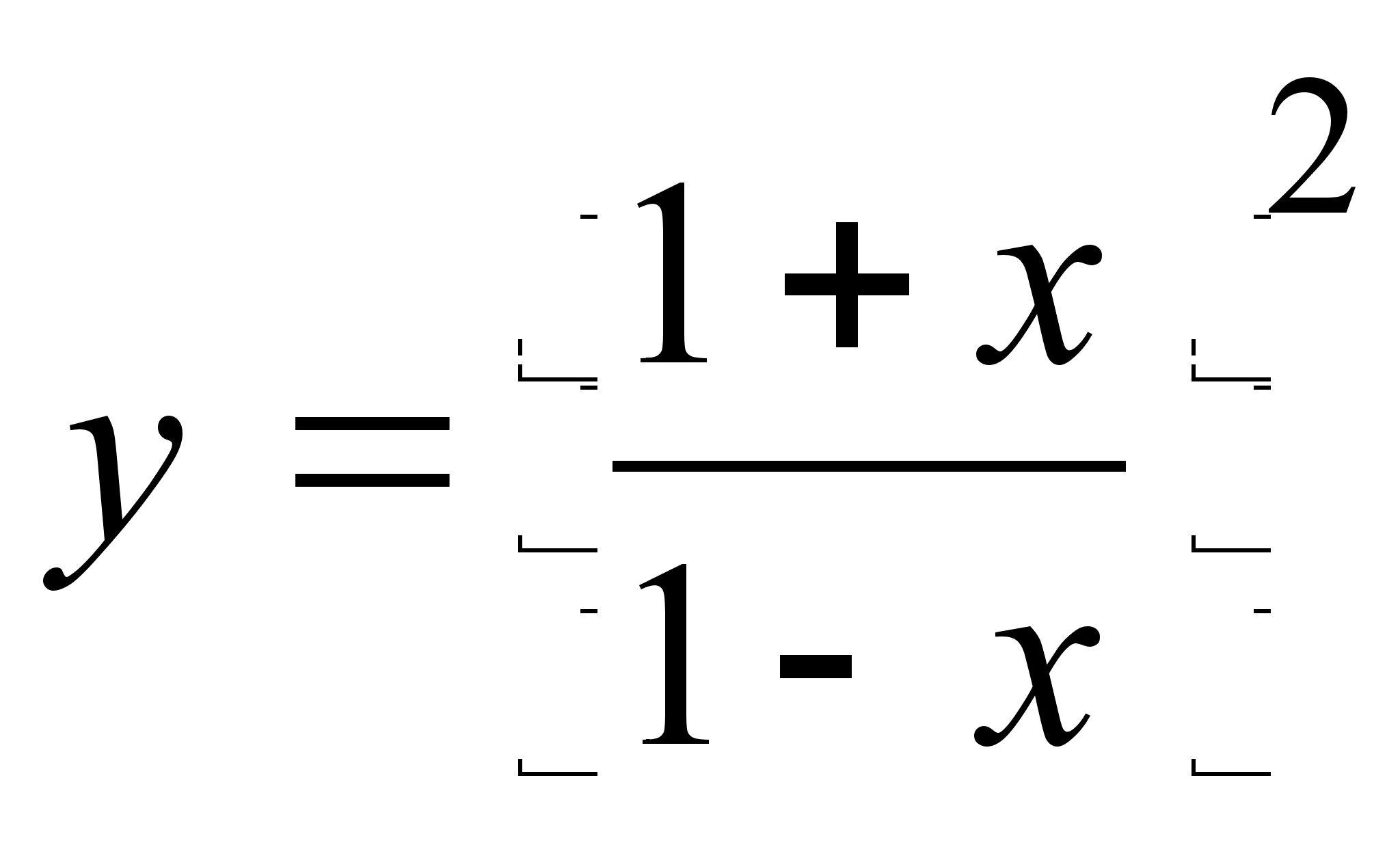 ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]()
21) ![]() ;
;
22) 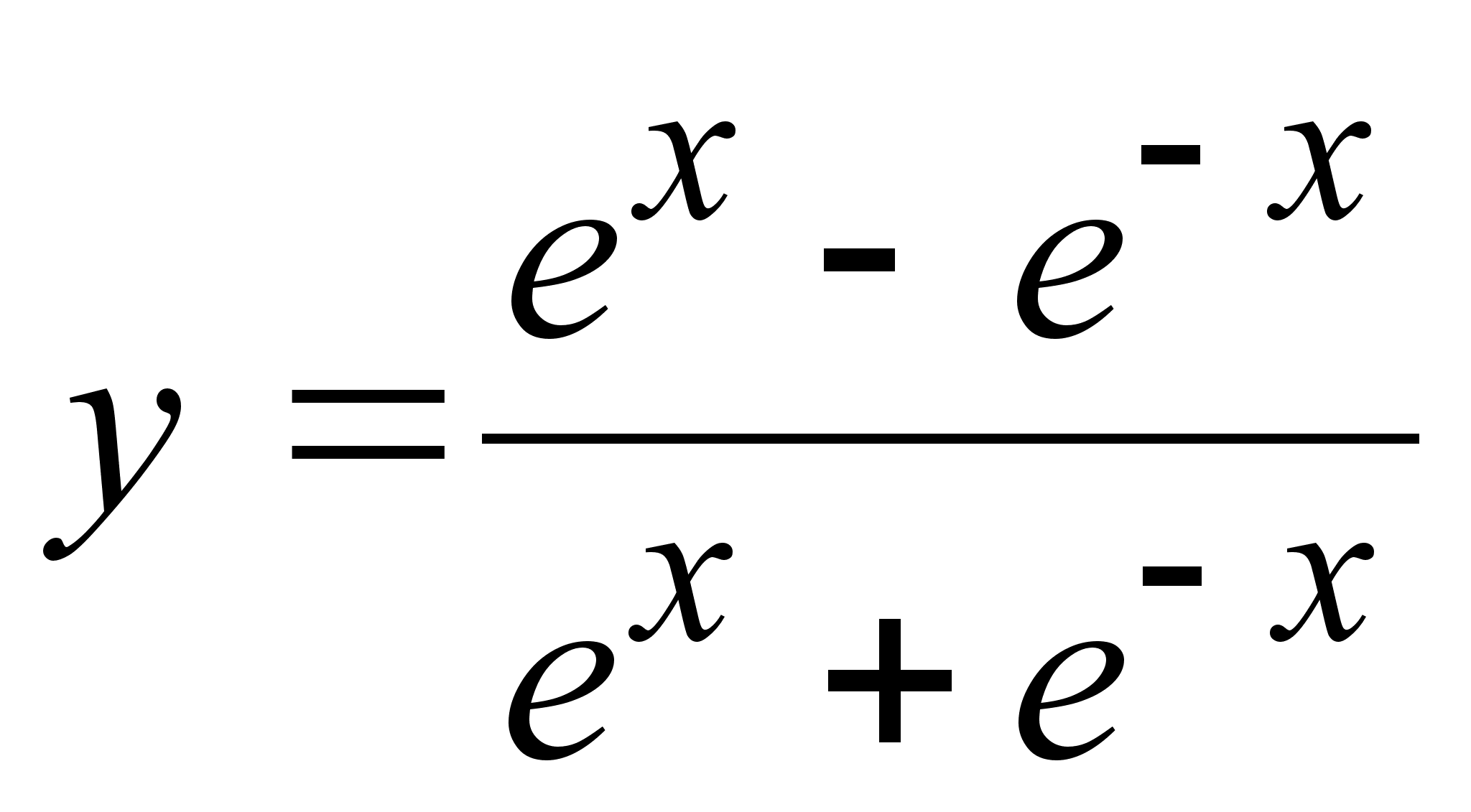 ;
;
23) ![]() ;
;
24) ![]() ;
;
25) ![]() ;
;
26) ![]() .
.
2. Определить угол наклона касательной к графику функции:
1)![]() при
при ![]() ;
;
2) ![]() при
при ![]() ;
;
3)![]() при
при ![]() ;
;
4)![]() при
при![]() .
.
3. Найти промежутки возрастания и убывания функций и их экстремумы:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
4. Найти эластичность функций:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
6) ![]() .
.
5. Для заданной зависимости спроса ![]() от цены
от цены ![]() найти эластичность спроса и вычислить ее при заданном значении
найти эластичность спроса и вычислить ее при заданном значении ![]() :
:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
6. Для заданной зависимости спроса ![]() от цены
от цены ![]() найти значения цены, при которых выручка возрастает с увеличением цены:
найти значения цены, при которых выручка возрастает с увеличением цены:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Ответы и решения
1.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) 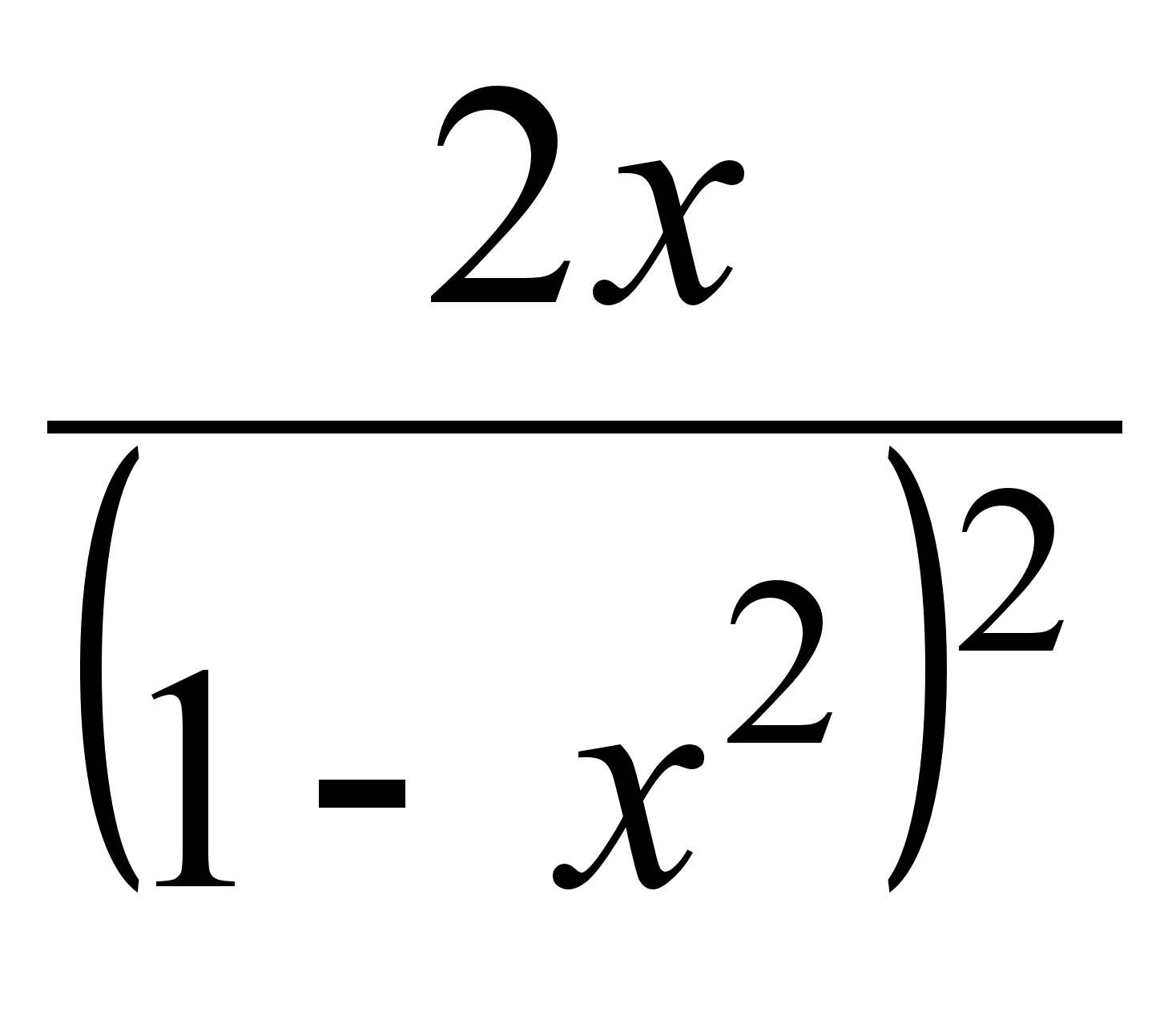 ;
;
11) 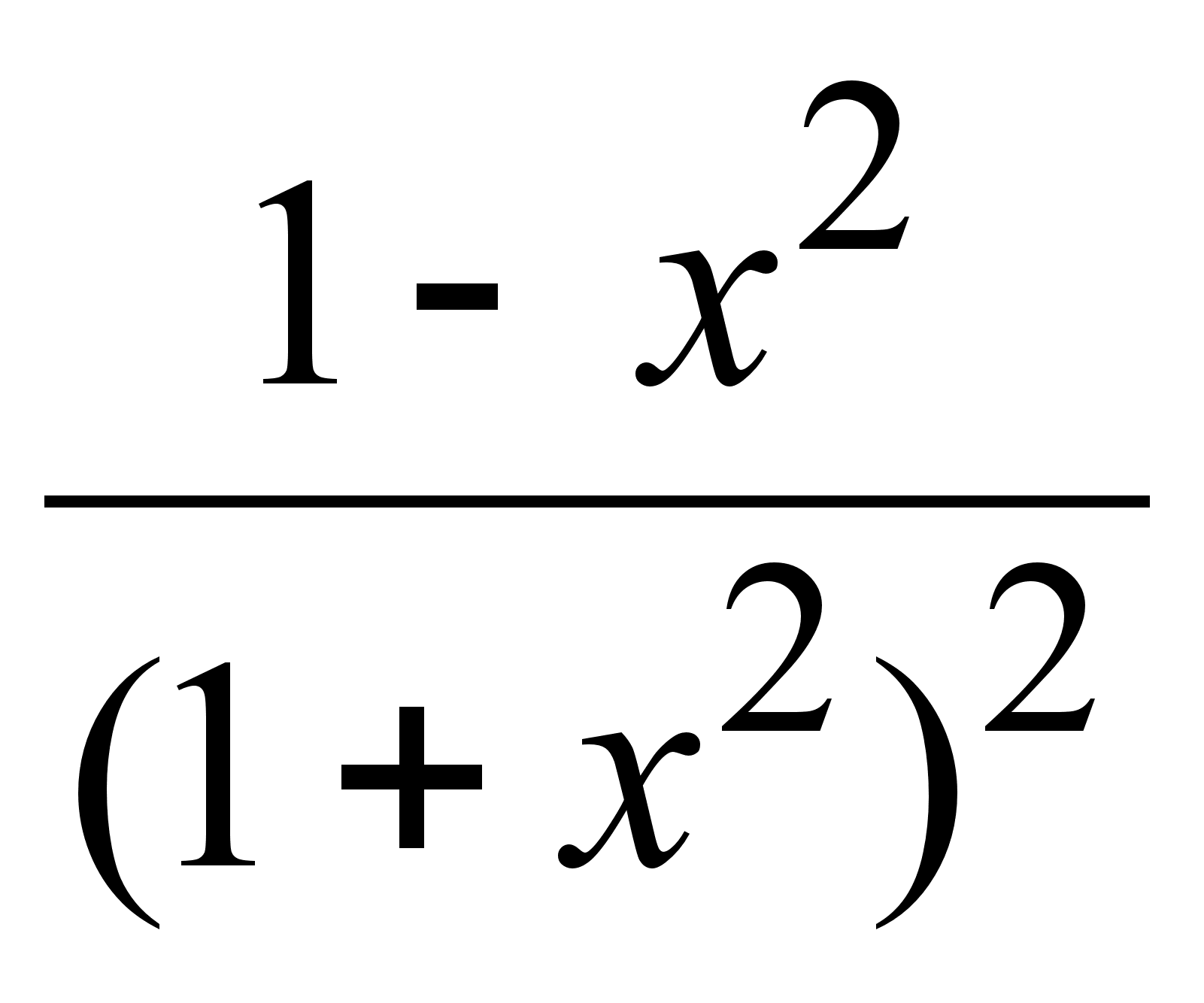 ;
;
12) 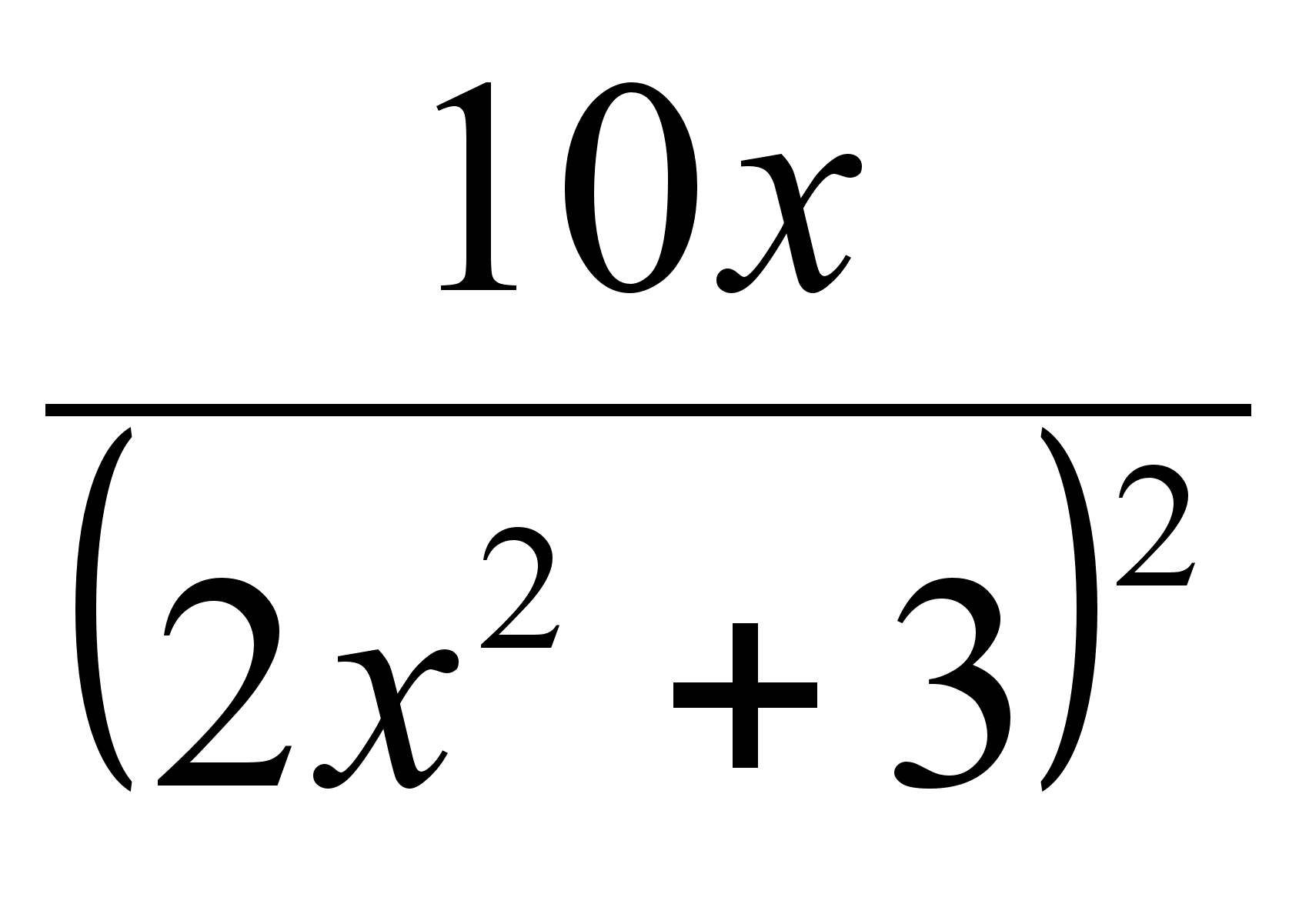 ;
;
13) ![]() ;
;
14) 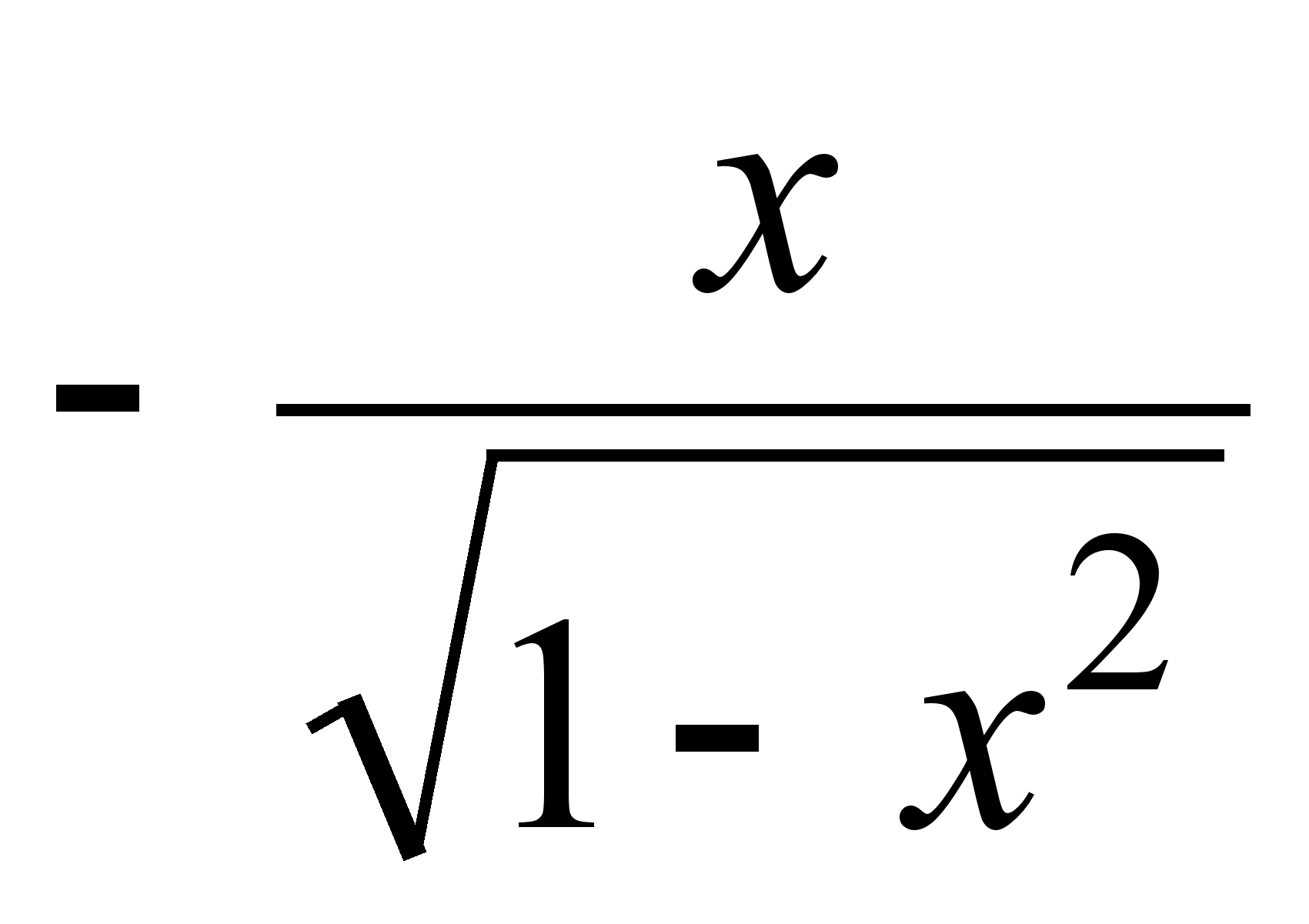 ;
;
15) 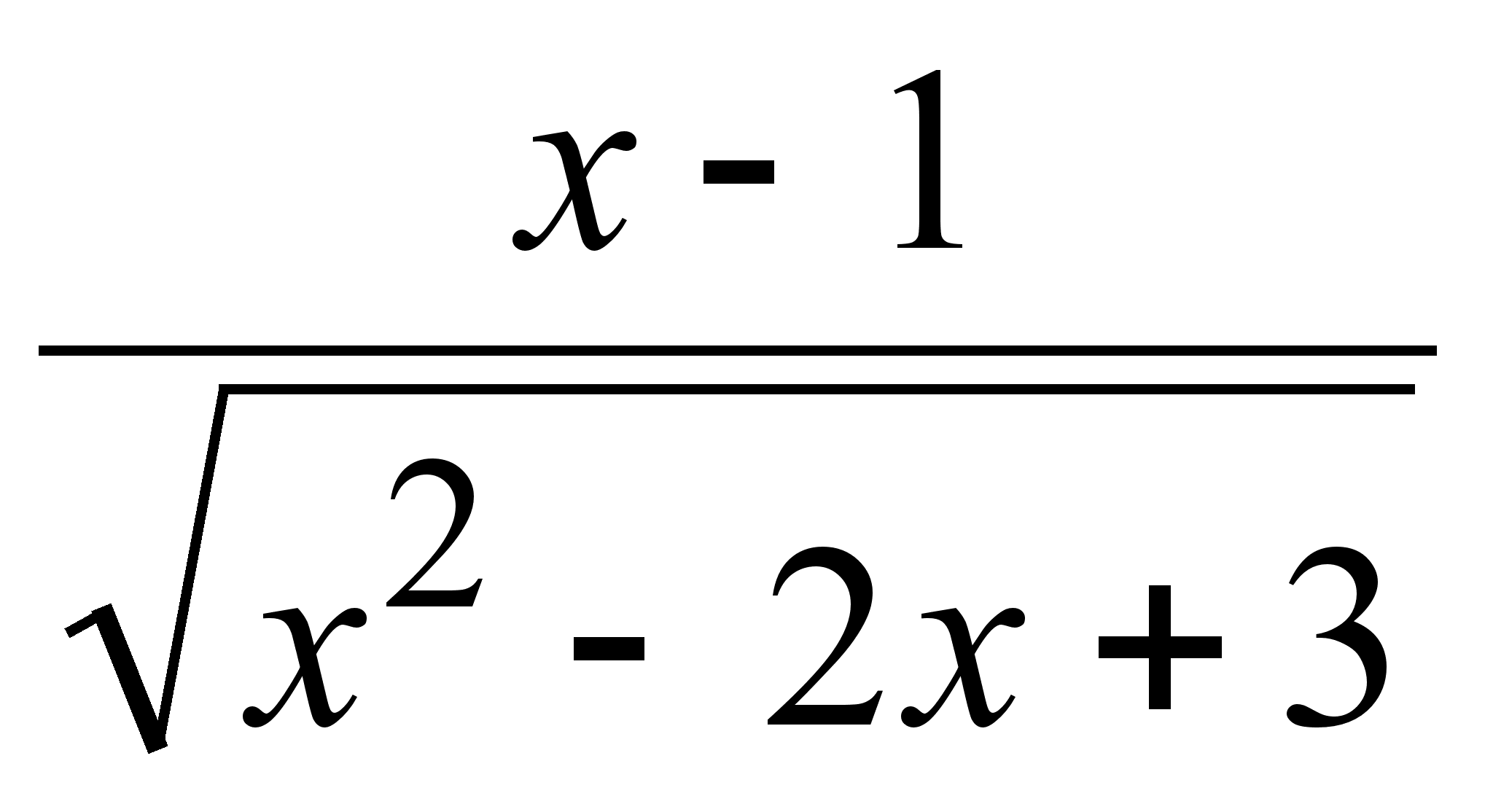 ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() ;
;
21) ![]() ;
;
22)  ;
;
23) ![]() ;
;
24) ![]() ;
;
25) ![]() ;
;
26) 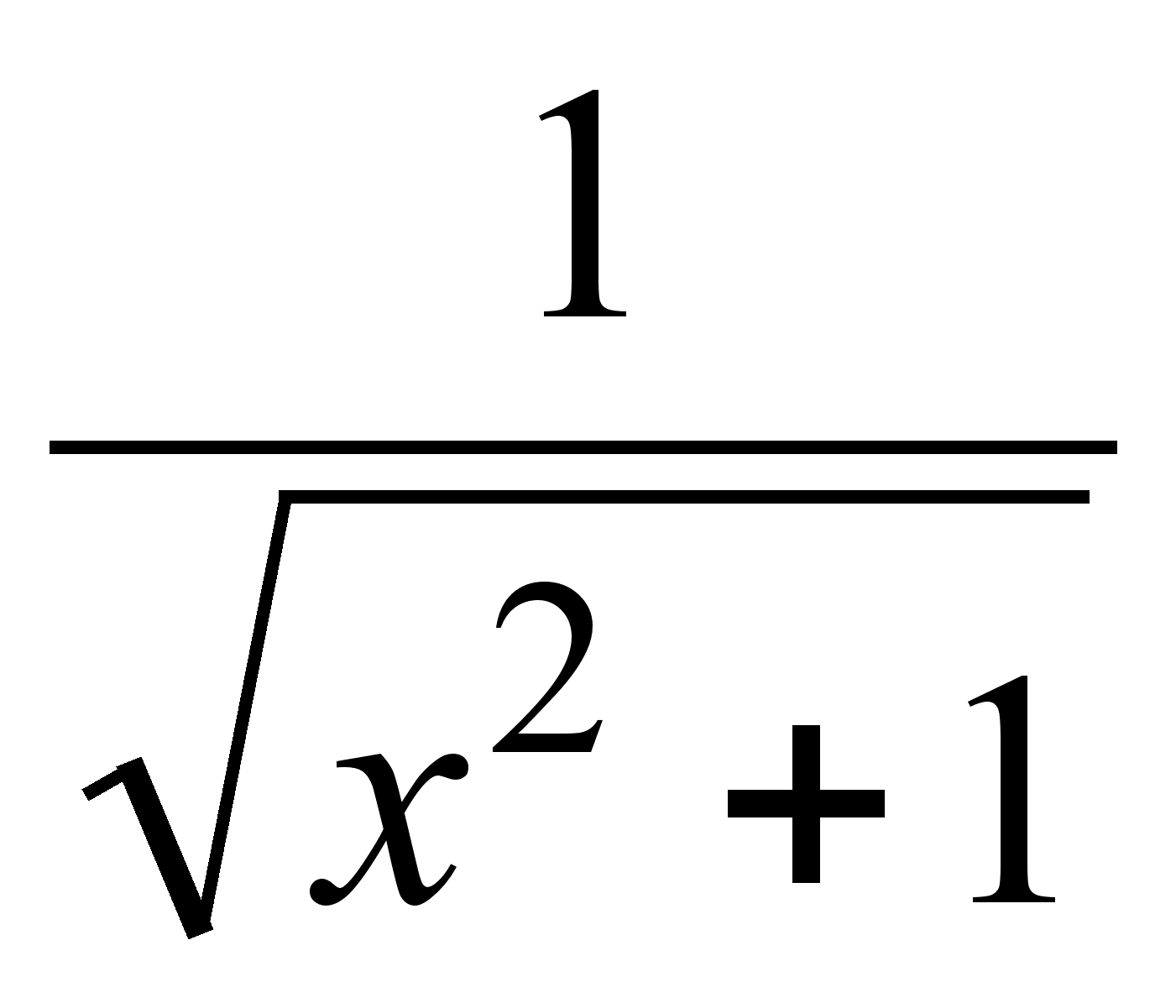 .
.
2.
1) Угол наклона касательной ![]() поскольку
поскольку![]() ;
;
2) ![]() ; 3)
; 3) ![]() , 4)
, 4) ![]() .
.
3.
1) При ![]() функция убывает, при
функция убывает, при ![]() - возрастает;
- возрастает; ![]() ;
;
2) Функция возрастает при ![]() и
и ![]() ; убывает при
; убывает при ![]() ;
; ![]() ;
; ![]() ;
;
3) Функция убывает при всех ![]() ; 4) Функция возрастает при всех
; 4) Функция возрастает при всех ![]() ;
;
5) Функция убывает при ![]() , возрастает при
, возрастает при ![]() ;
;
![]() ;
;
6) Функция убывает при всех ![]() ;
;
7) Функция возрастает при ![]() , убывает при
, убывает при ![]() ;
; ![]() ;
;
8) Функция убывает при ![]() и
и ![]() , возрастает при
, возрастает при ![]() ;
;
![]() ,
, ![]() ;
;
9) Функция возрастает при ![]() , убывает при
, убывает при ![]() ;
;![]() ;
;
10) Функция убывает при ![]() , возрастает при
, возрастает при ![]() ;
; ![]() ;
;
4.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() .
.
5. 1) ![]() ,
, ![]() ; спрос нейтрален; 2)
; спрос нейтрален; 2) ![]() ,
, ![]() ; спрос эластичен; 3)
; спрос эластичен; 3) 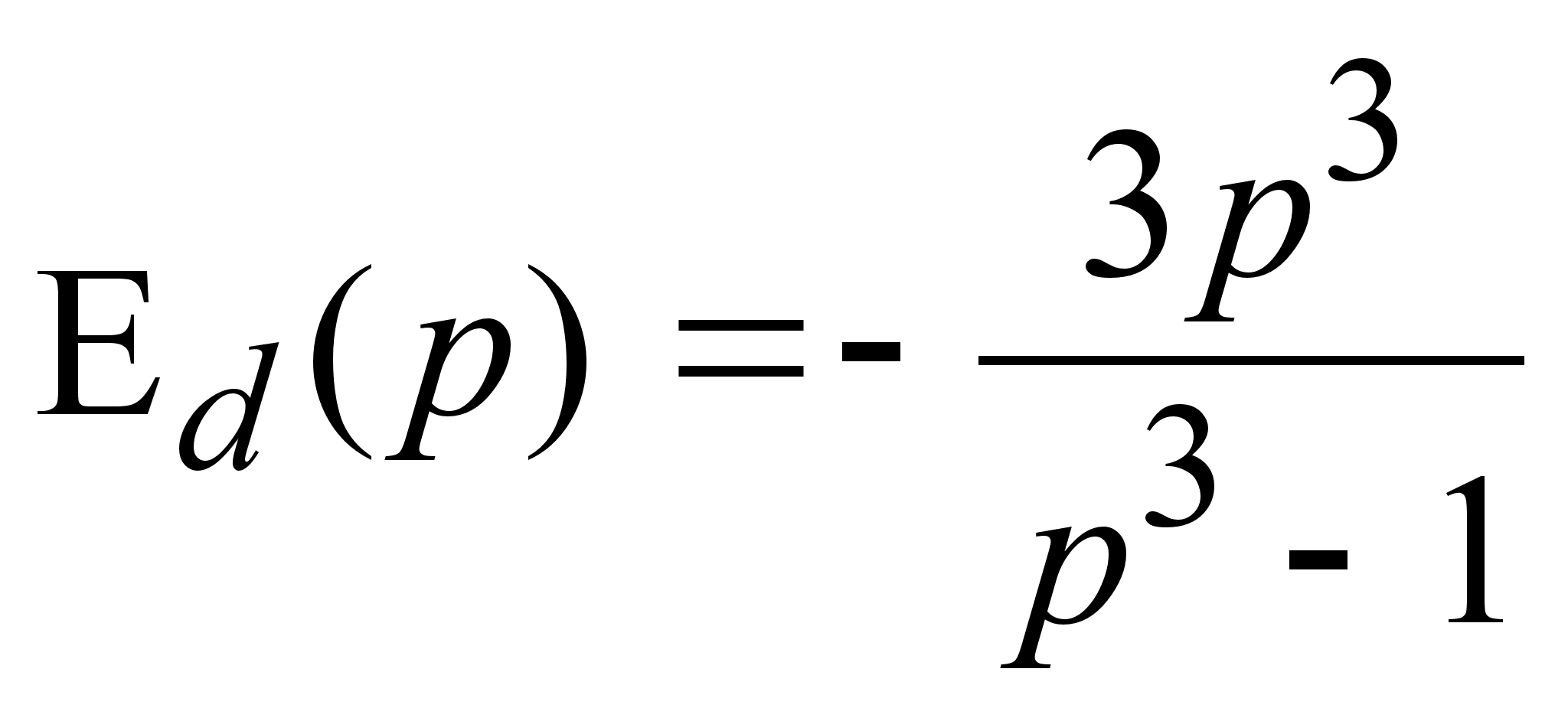 ,
, ![]() ; спрос неэластичен.
; спрос неэластичен.
6. 1) ![]() ; 2)
; 2) ![]() ; 3) Таких значений цены нет; выручка не меняется с ростом цены.
; 3) Таких значений цены нет; выручка не меняется с ростом цены.
§ 4. Неопределенный интеграл
К понятию неопределенного интеграла приводит задача о нахождении функции по ее производной. Эта задача решается с помощью операции интегрирования, обратной по отношению к операции дифференцирования.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
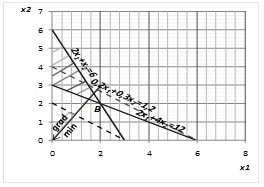
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





0 комментариев