Навигация
4. Обратная функция
Рассмотрим
функцию ![]() с областью
определения
с областью
определения ![]() и множеством
значений
и множеством
значений ![]() .
Предположим,
что для любого
.
Предположим,
что для любого
![]() уравнение
уравнение ![]() имеет единственное
решение
имеет единственное
решение![]() .
Тогда на множестве
.
Тогда на множестве
![]() можно определить
функцию, сопоставляющую
каждому
можно определить
функцию, сопоставляющую
каждому ![]() такое значение
такое значение
![]() ,
что
,
что ![]() .
Эту функцию
называют обратной
для функции
.
Эту функцию
называют обратной
для функции
![]() и обозначают
и обозначают
![]() :
:
![]() .
.
Функцию, у которой существует обратная функция, назовем обратимой.
Обозначая, как
обычно, аргумент
функции через
![]() ,
а значение
функции через
,
а значение
функции через
![]() ,
можно записать
,
можно записать
![]() .
.
Поскольку
взаимная перестановка
переменных
![]() и
и ![]() равносильна
переобозначению
координатных
осей, можно
показать, что
график функции
равносильна
переобозначению
координатных
осей, можно
показать, что
график функции
![]() симметричен
графику функции
симметричен
графику функции
![]() относительно
биссектрисы
первого и третьего
координатных
углов (то есть
относительно
прямой
относительно
биссектрисы
первого и третьего
координатных
углов (то есть
относительно
прямой ![]() ).
).

Примеры.
1) Для линейной
функции ![]() обратная функция
также линейна
и имеет вид
обратная функция
также линейна
и имеет вид ![]() .
Меняя местами
.
Меняя местами
![]() и
и ![]() ,
получаем
,
получаем ![]() .
Графики исходной
и обратной
функций приведены
на рис. 10.
.
Графики исходной
и обратной
функций приведены
на рис. 10.
Рис. 10.
2) Для функции
![]() ,
,
![]() ,
множество
значений имеет
вид
,
множество
значений имеет
вид ![]() .
Для каждого
.
Для каждого
![]() уравнение
уравнение ![]() имеет единственное
решение
имеет единственное
решение ![]() .
Поменяв местами
.
Поменяв местами
![]() и
и ![]() ,
получим
,
получим ![]() ,
,
![]() .
Графики функций
приведены на
рис. 11 .
.
Графики функций
приведены на
рис. 11 .
Рис. 11.
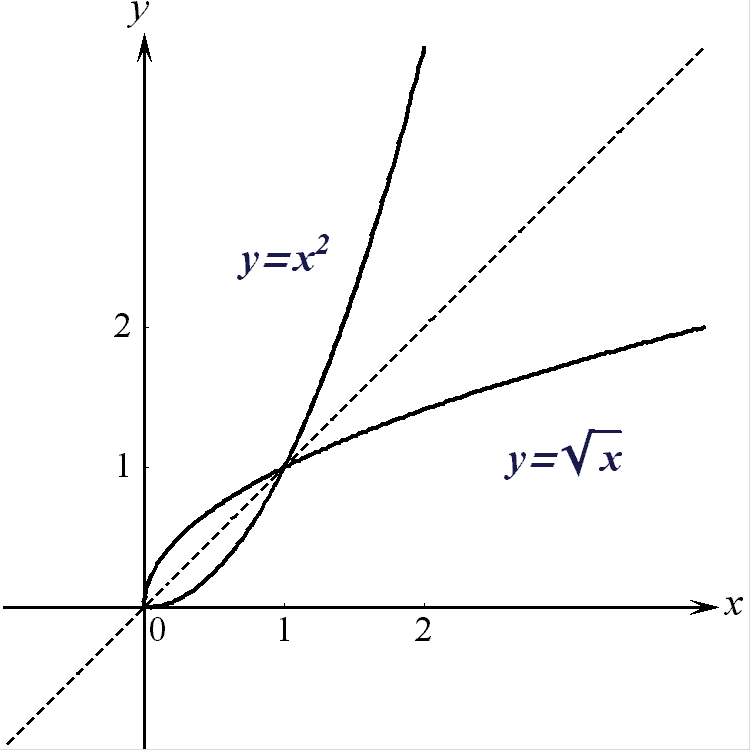
Рис. 11.
3) Обратной к
показательной
функции ![]() является
логарифмическая
функция
является
логарифмическая
функция ![]() .
На рис. 12 представлены
графики функций
.
На рис. 12 представлены
графики функций
![]() и
и ![]() .
.
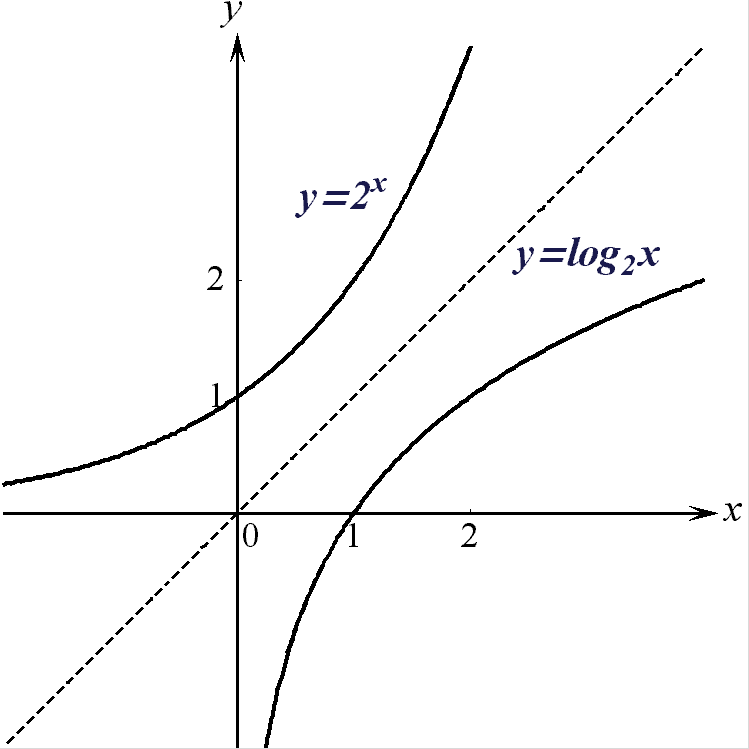
Рис. 12.
Упражнения
1. Найти области определения следующих функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) 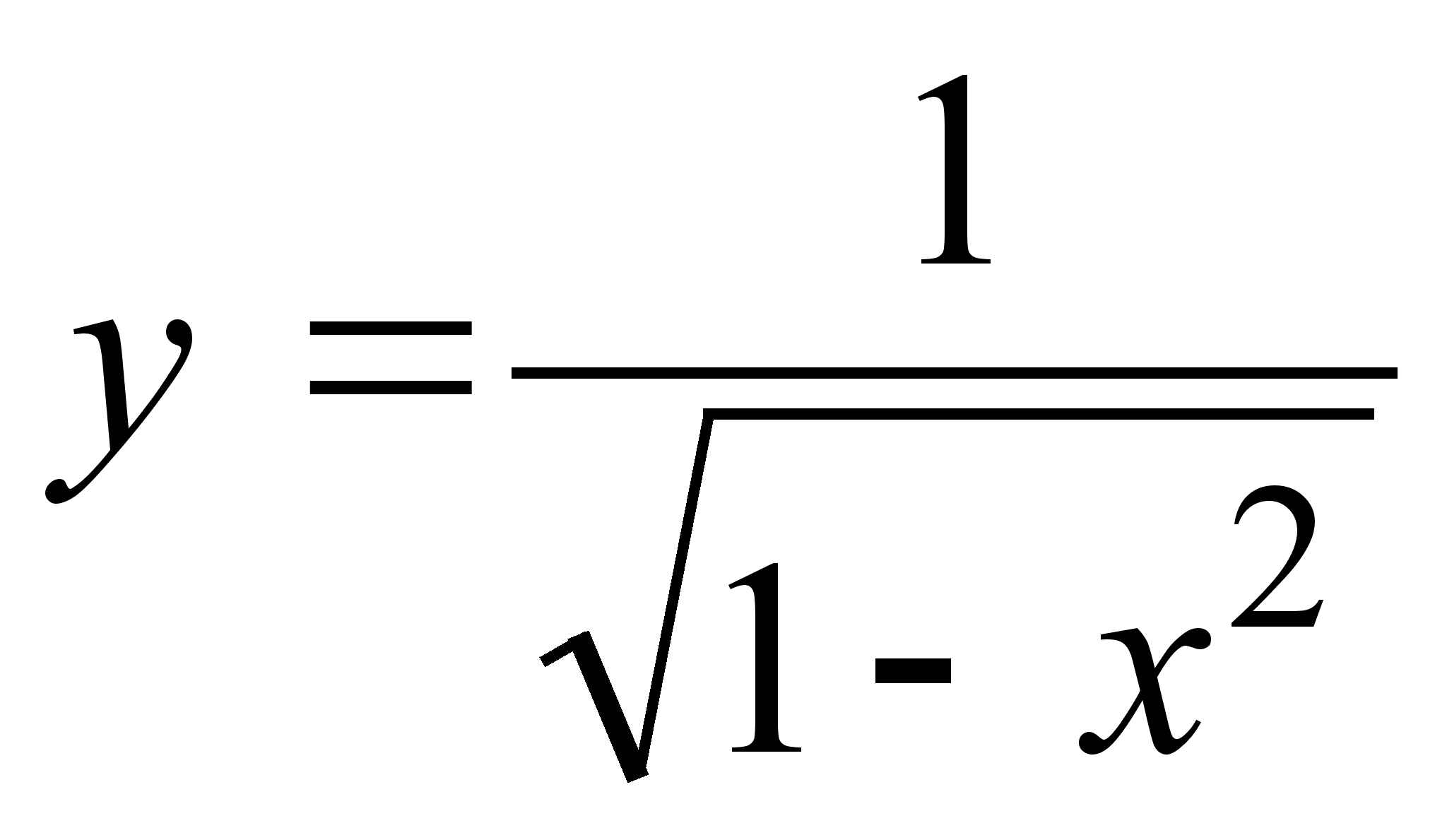 ;
;
18) 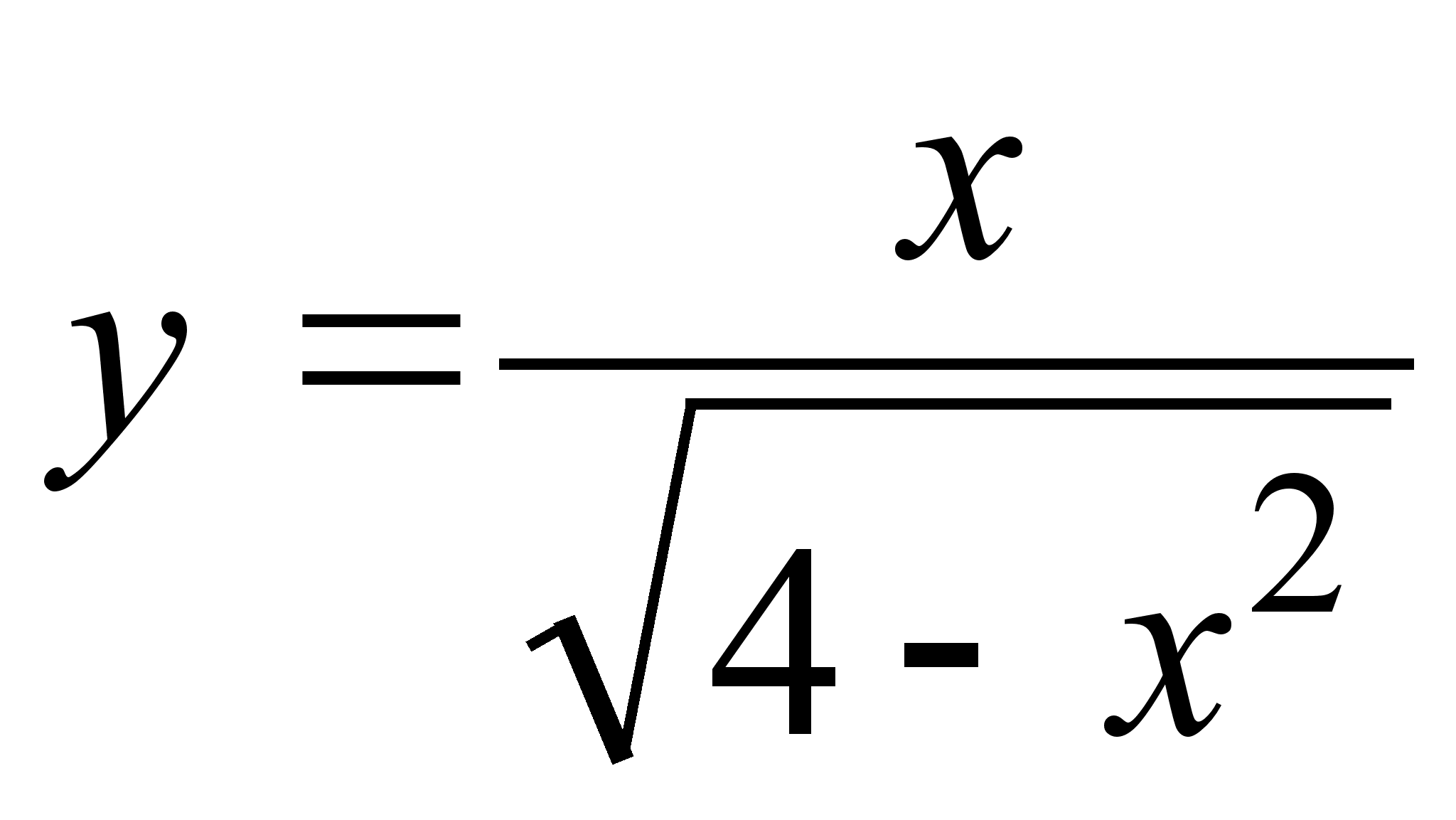 ;
;
19)  ;
;
20) 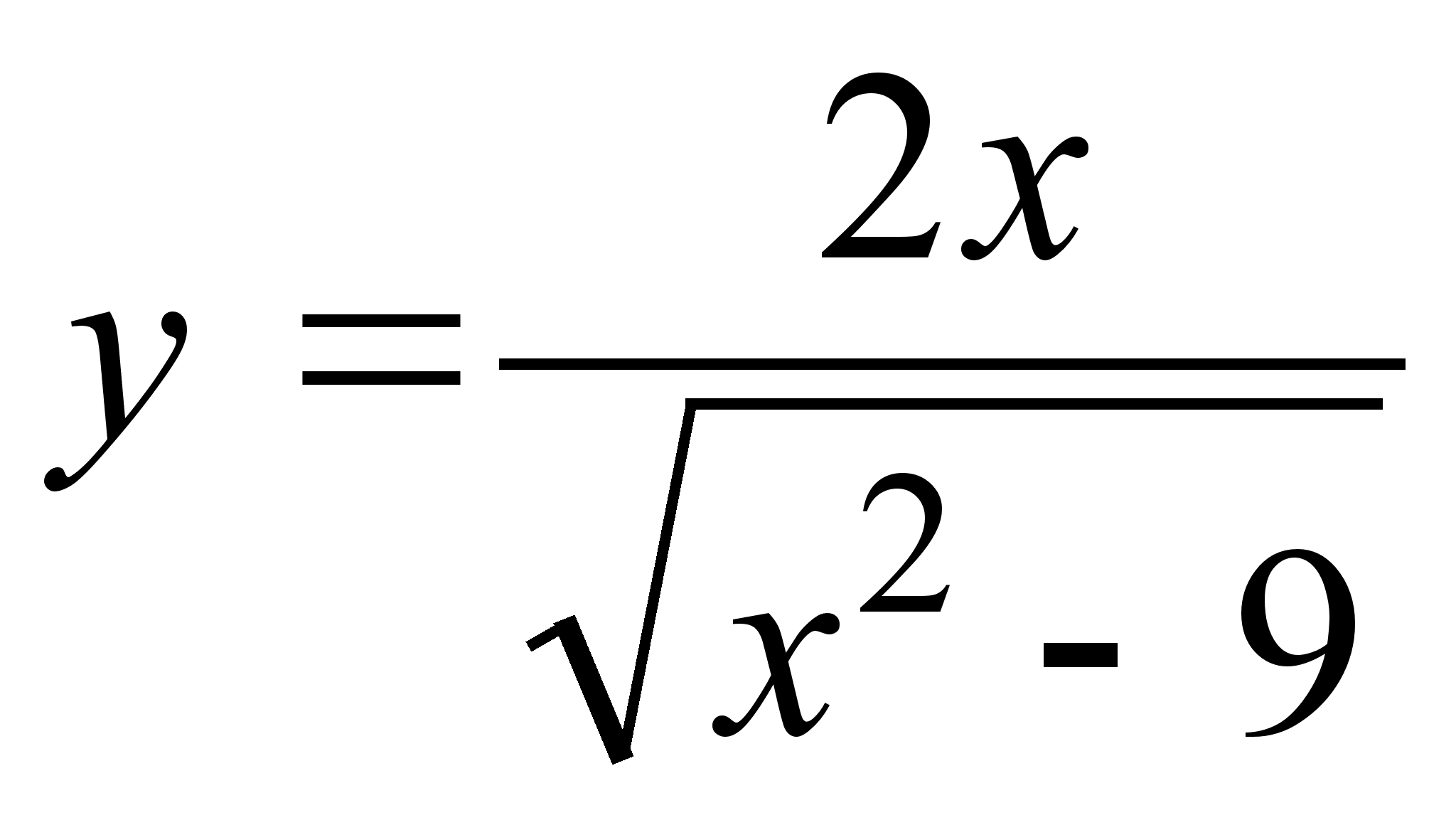 ;
;
21) ![]() ;
;
22) ![]() .
.
2. Построить графики функций:
1) ![]() ,
,
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ,
,
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() .
.
3. Найти функции обратные к функции ![]() , указать их области определения и построить графики:
, указать их области определения и построить графики:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ,
, ![]() ;
;
4) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() .
.
Ответы
1.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() R;
R;
6) ![]() R;
R;
7) ![]() ;
;
8); ![]()
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() R;
R;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() ;
;
21) ![]() ;
;
22)![]() .
.
.
3.
1) ![]() ,
, ![]() R;
R;
2) ![]() ,
, ![]() R;
R;
3)![]() ,
, ![]() ;
;
4) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() ;
;
6) ![]() ,
, ![]() ;
;
7) ![]() ,
, ![]() ;
;
8) ![]() ;
;
9) ![]() ,
, ![]() ;
;
10) ![]() ,
, ![]() R.
R.
§ 2. Предел и непрерывность функции
Пределом функции в точке называется число, к которому приближаются значения функции при приближении аргумента к этой точке. Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл.
Предел последовательности
Последовательностью
называется
функция, определенная
на множестве
натуральных
чисел N = ![]() .
Значения этой
функции
.
Значения этой
функции ![]() ,
,
![]() N, называются
элементами
или членами
последовательности,
число
N, называются
элементами
или членами
последовательности,
число ![]() называется
номером элемента
называется
номером элемента ![]() .
Для последовательностей
используется
обозначение
.
Для последовательностей
используется
обозначение ![]() или более наглядная
запись
или более наглядная
запись ![]() .
Задать последовательность
можно с помощью
формулы, связывающей
.
Задать последовательность
можно с помощью
формулы, связывающей
![]() и
и ![]() .
.
Приведем примеры последовательностей, указав их различные представления:
а) ![]() , или
, или
![]() , или
, или
![]() ;
;
б) ![]() , или
, или
![]() , или
, или
![]() ;
;
в) ![]() , или
, или ![]() , или
, или
![]() .
.
Заметим,
что элементы
этих последовательностей
ведут себя
по-разному с
увеличением
номера ![]() :
в первом случае
убывают, приближаясь
к нулю; во втором
случае неограниченно
возрастают;
в третьем случае
не приближаются
ни к какому
определенному
числу, принимая
поочередно
значения
:
в первом случае
убывают, приближаясь
к нулю; во втором
случае неограниченно
возрастают;
в третьем случае
не приближаются
ни к какому
определенному
числу, принимая
поочередно
значения ![]() и
и ![]() .
Для описания
поведения
элементов
последовательности
при неограниченном
увеличении
n вводится
понятие предела.
.
Для описания
поведения
элементов
последовательности
при неограниченном
увеличении
n вводится
понятие предела.
Число а называется
пределом
последовательности
![]() ,
если для любого
положительного
числа
,
если для любого
положительного
числа ![]() существует
такой номер
существует
такой номер
![]() ,
что для всех
,
что для всех
![]() выполняется
неравенство
выполняется
неравенство
![]() (то есть
(то есть ![]() отличается
от
отличается
от ![]() менее, чем на
менее, чем на
![]() ).
).
Если предел
существует,
то говорят, что
последовательность
сходится, и
пишут ![]() (читается: “предел
(читается: “предел
![]() равен
равен ![]() ”)
или
”)
или ![]() при
при ![]() (“
(“![]() стремится к
стремится к
![]() при
при ![]() ,
стремящемся
к бесконечности”).
В противном
случае говорят,
что последовательность
расходится.
,
стремящемся
к бесконечности”).
В противном
случае говорят,
что последовательность
расходится.
Примеры. а)
Последовательность
![]() сходится,
ее предел равен
нулю:
сходится,
ее предел равен
нулю: ![]() .
Это непосредственно
следует из
определения
предела, поскольку
при любом
.
Это непосредственно
следует из
определения
предела, поскольку
при любом ![]() неравенство
неравенство
![]() выполняется
для всех
выполняется
для всех ![]() ,
и в качестве
,
и в качестве
![]() можно взять
любое натуральное
число, большее
можно взять
любое натуральное
число, большее
![]() .
.
б) Аналогично доказывается более общее утверждение:
![]() при любом
при любом
![]() .
.
Например,
![]() ,
,
![]() и т. д.
и т. д.
Правила вычисления пределов последовательностей
При вычислении пределов последовательностей используются следующие правила:
I. Если
последовательности
![]() и
и ![]() сходятся, то
сходятся их
сумма, разность
и произведение,
причем:
сходятся, то
сходятся их
сумма, разность
и произведение,
причем:
1) ![]() ,
,
2) ![]() ,
,
3) ![]() ;
;
если ![]() и
и ![]() ,
то сходится
также и частное:
,
то сходится
также и частное:
4) 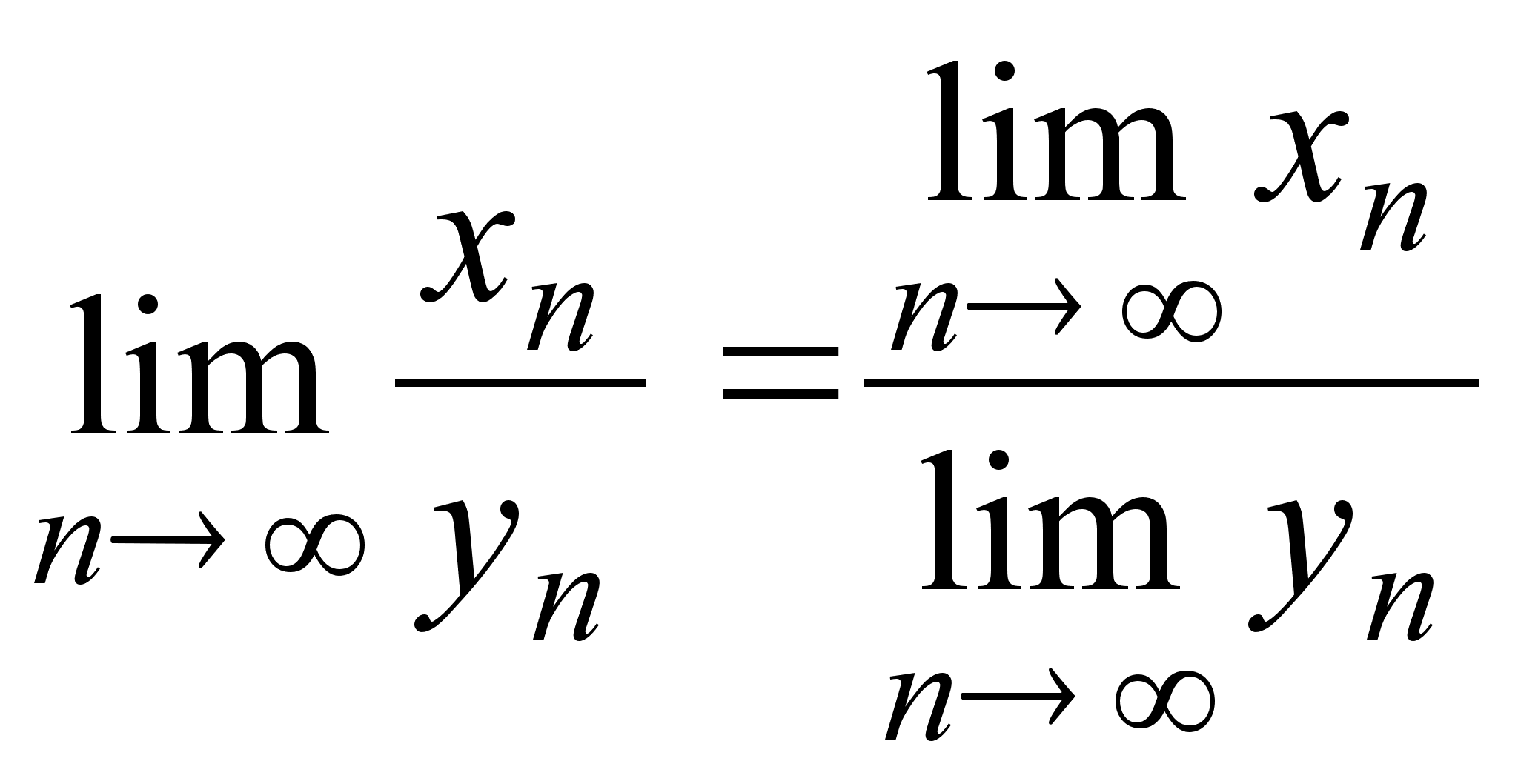 .
.
II. Предел
последовательности
![]() ,
где
,
где ![]() - постоянная,
равен этой
постоянной:
- постоянная,
равен этой
постоянной:
![]() .
.
III. Постоянный множитель можно выносить за знак предела:
![]()
(следствие правил I.3 и II).
Применению указанных правил часто предшествуют некоторые предварительные преобразования выражения, стоящего под знаком предела.
Примеры. а) 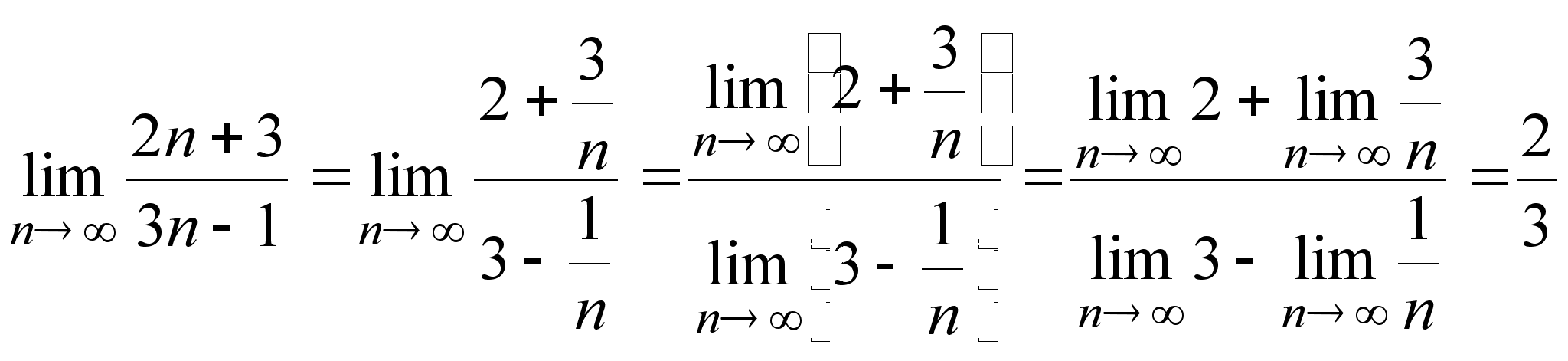 ;
;
б) 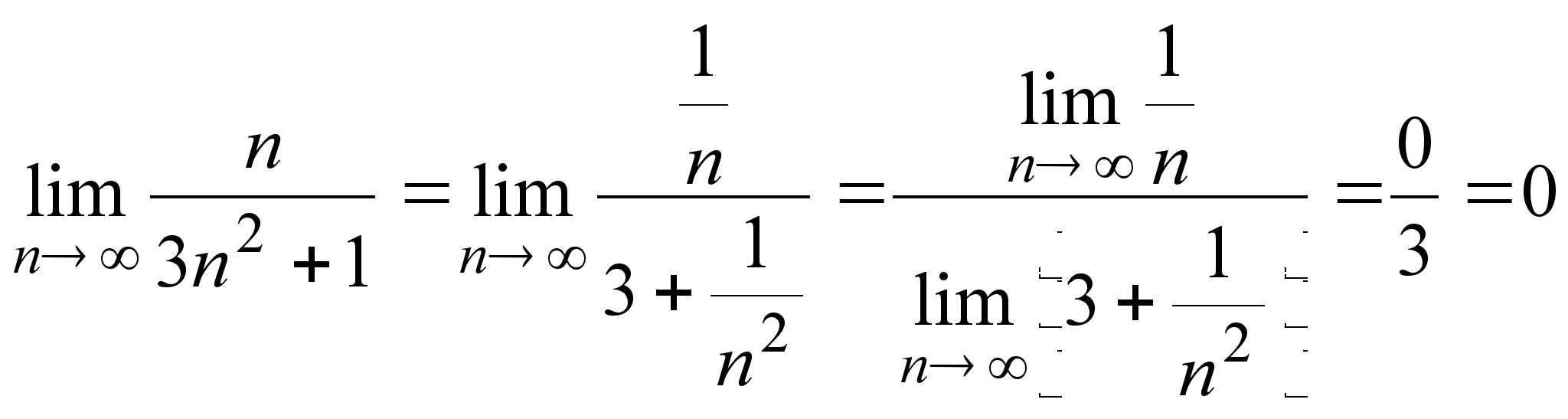 .
.
Бесконечно малые и бесконечно большие последовательности
Последовательность ![]() называется
бесконечно
малой, если
называется
бесконечно
малой, если
![]() .
Это означает,
что для любого
.
Это означает,
что для любого
![]() найдется номер
найдется номер
![]() такой, что для
всех
такой, что для
всех ![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Последовательность
![]() называется
бесконечно
большой, если
для любого
числа
называется
бесконечно
большой, если
для любого
числа ![]() найдется такой
номер
найдется такой
номер ![]() ,
что для всех
,
что для всех
![]() справедливо
неравенство
справедливо
неравенство
![]() .
В этом случае
пишут
.
В этом случае
пишут ![]() (читается: “предел
(читается: “предел
![]() равен бесконечности”)
или
равен бесконечности”)
или ![]() при
при ![]() (“
(“![]() стремится к
бесконечности
при
стремится к
бесконечности
при ![]() ,
стремящемся
к бесконечности”).
Если при этом
все элементы
,
стремящемся
к бесконечности”).
Если при этом
все элементы
![]() положительны,
начиная с некоторого
номера, то пишут
положительны,
начиная с некоторого
номера, то пишут
![]() (“предел
(“предел ![]() равен плюс
бесконечности”),
а если отрицательны
- используют
запись
равен плюс
бесконечности”),
а если отрицательны
- используют
запись ![]() (“предел
(“предел ![]() равен минус
бесконечности”).
равен минус
бесконечности”).
Заметим, что
если ![]() ,
то
,
то ![]() (при
(при ![]() ),
то есть последовательность,
обратная к
бесконечно
большой, является
бесконечно
малой. Аналогично,
если
),
то есть последовательность,
обратная к
бесконечно
большой, является
бесконечно
малой. Аналогично,
если ![]() ,
то
,
то ![]() (при
(при ![]() ),
– последовательность,
обратная к
бесконечно
малой, является
бесконечно
большой.
),
– последовательность,
обратная к
бесконечно
малой, является
бесконечно
большой.
Справедливы также следующие утверждения:
сумма и произведение двух бесконечно малых последовательностей являются бесконечно малыми последовательностями;
произведение двух бесконечно больших последовательностей является бесконечно большой последовательностью;
если оба предела
![]() и
и ![]() равны
равны ![]() (или
(или ![]() ),
то
),
то ![]() (соответственно
(соответственно
![]() ).
).
Примеры. а) Последовательности
![]() ,
,
![]() ,
,
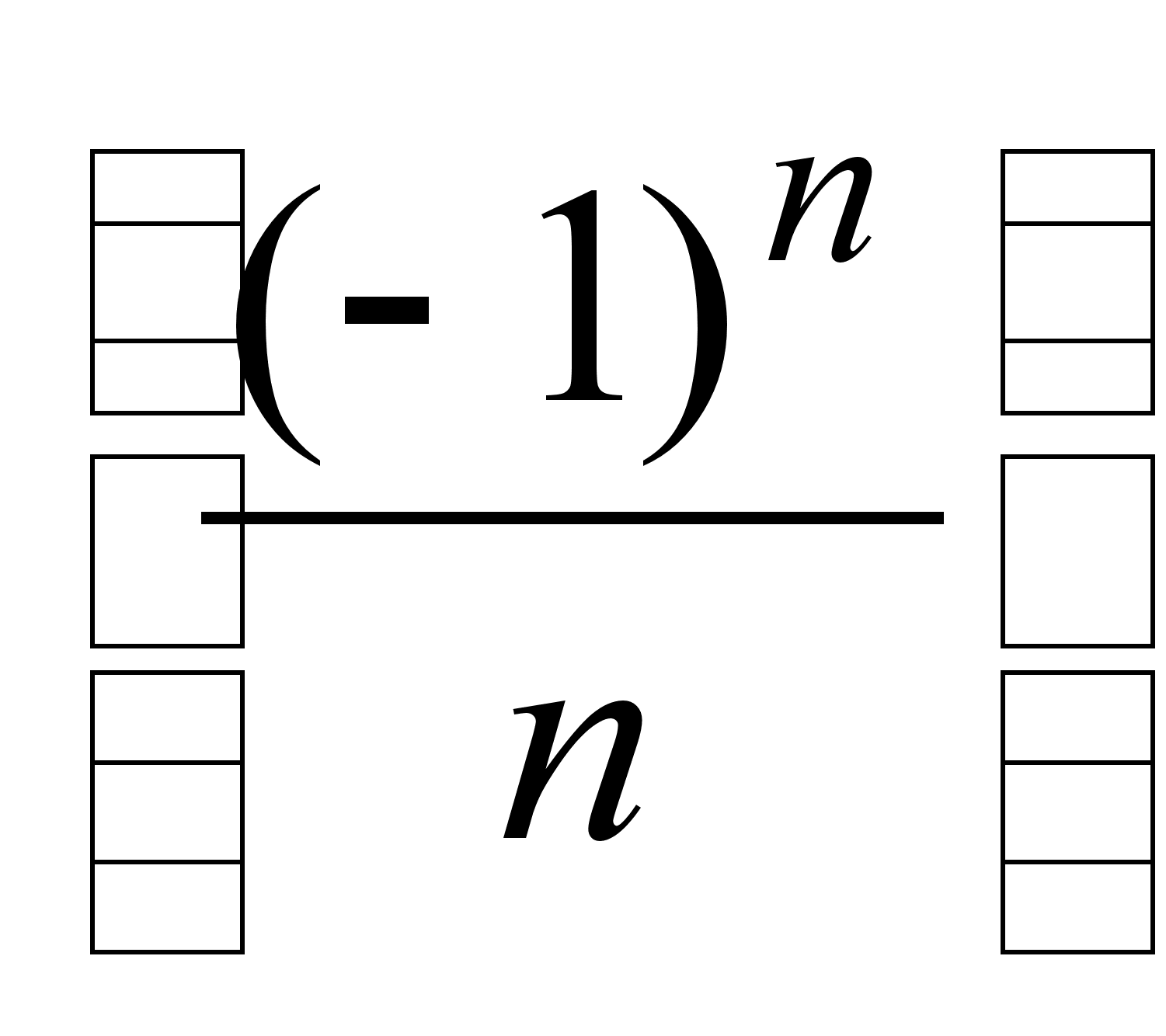 ,
,
![]() при
при ![]() ,
,
![]()
являются бесконечно малыми, а обратные к ним последовательности
{![]() },
{
},
{![]() },
{
},
{![]() },
{
},
{![]() }
при
}
при ![]() ,
{
,
{![]() }
}
– бесконечно большими.
б) Последовательности
![]() и
и ![]() бесконечно
большие, поэтому
их сумма
бесконечно
большие, поэтому
их сумма ![]() – также бесконечно
большая. Отсюда
следует, что
– также бесконечно
большая. Отсюда
следует, что
![]() – бесконечно
малая последовательность,
поскольку
– бесконечно
малая последовательность,
поскольку
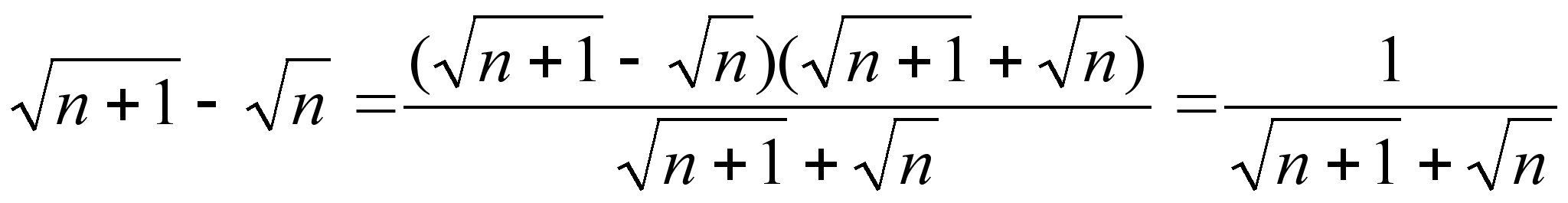 .
.
Число e
Рассмотрим
последовательность
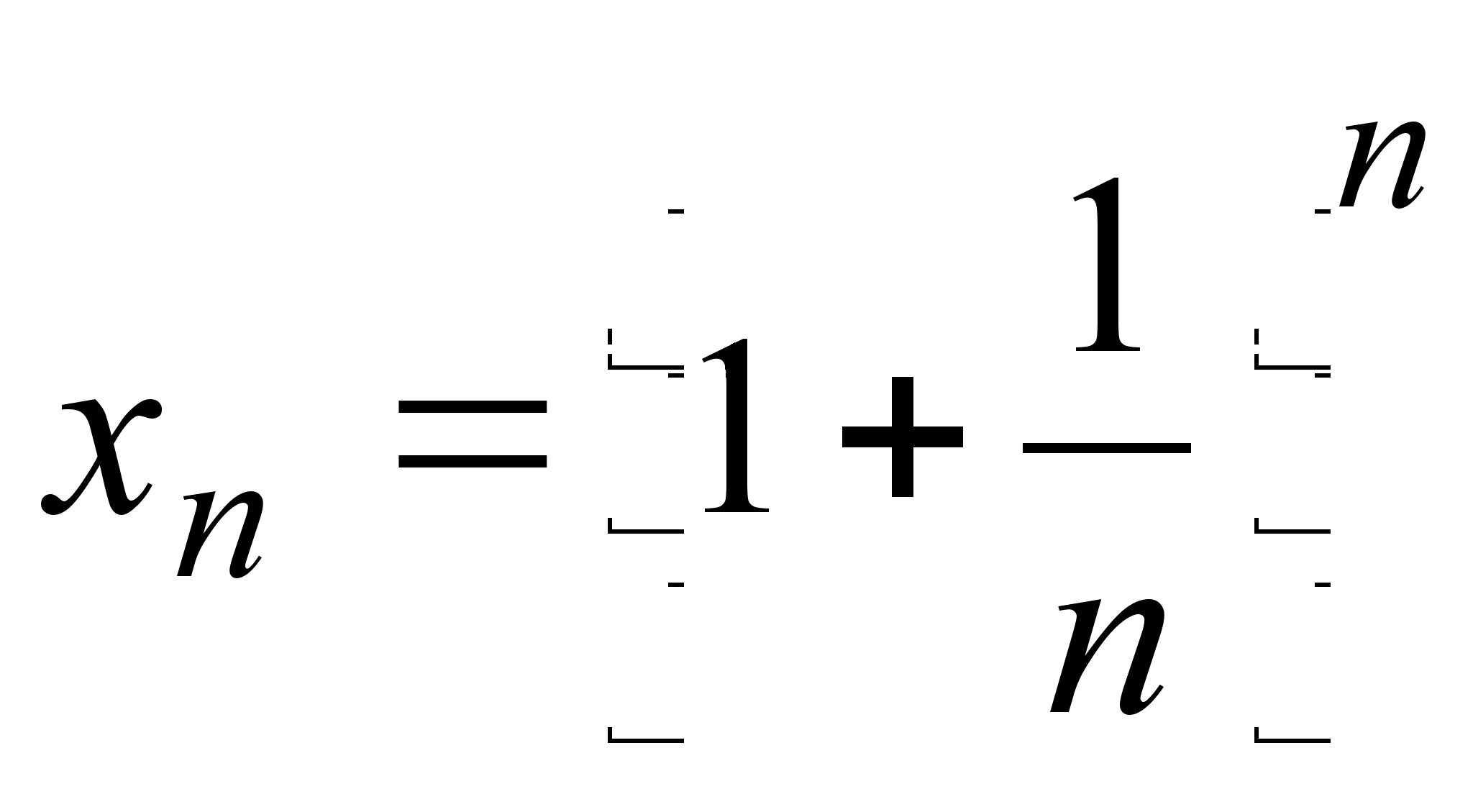 .
Можно показать,
что эта последовательность
сходится; ее
предел обозначается
буквой
.
Можно показать,
что эта последовательность
сходится; ее
предел обозначается
буквой ![]() :
:
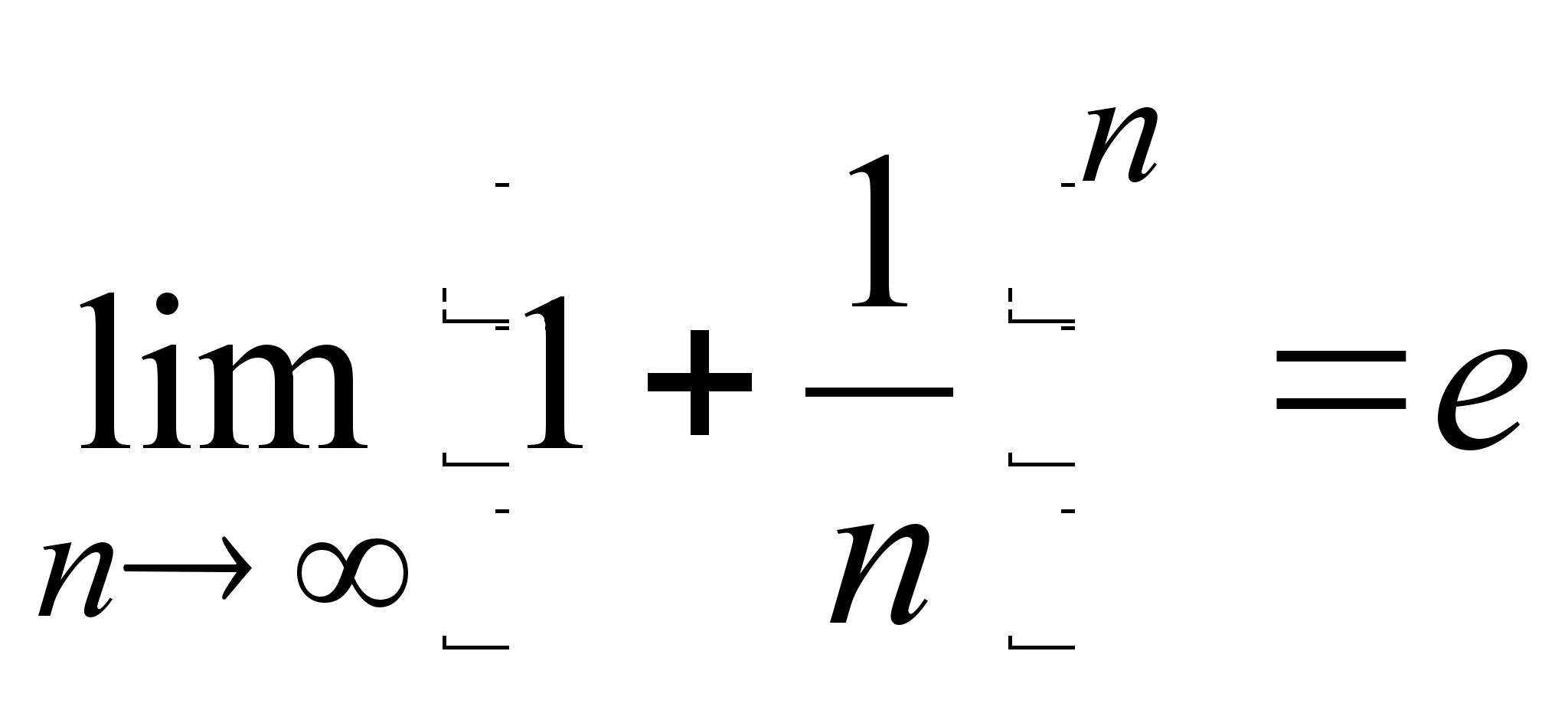 .
.
Число
![]() играет важную
роль в математике
(служит основанием
натуральных
логарифмов);
оно не является
рациональным
и приближенно
равно
играет важную
роль в математике
(служит основанием
натуральных
логарифмов);
оно не является
рациональным
и приближенно
равно
![]() .
.
Исходя
из определения
числа ![]() ,
можно получить
более общую
формулу:
,
можно получить
более общую
формулу:
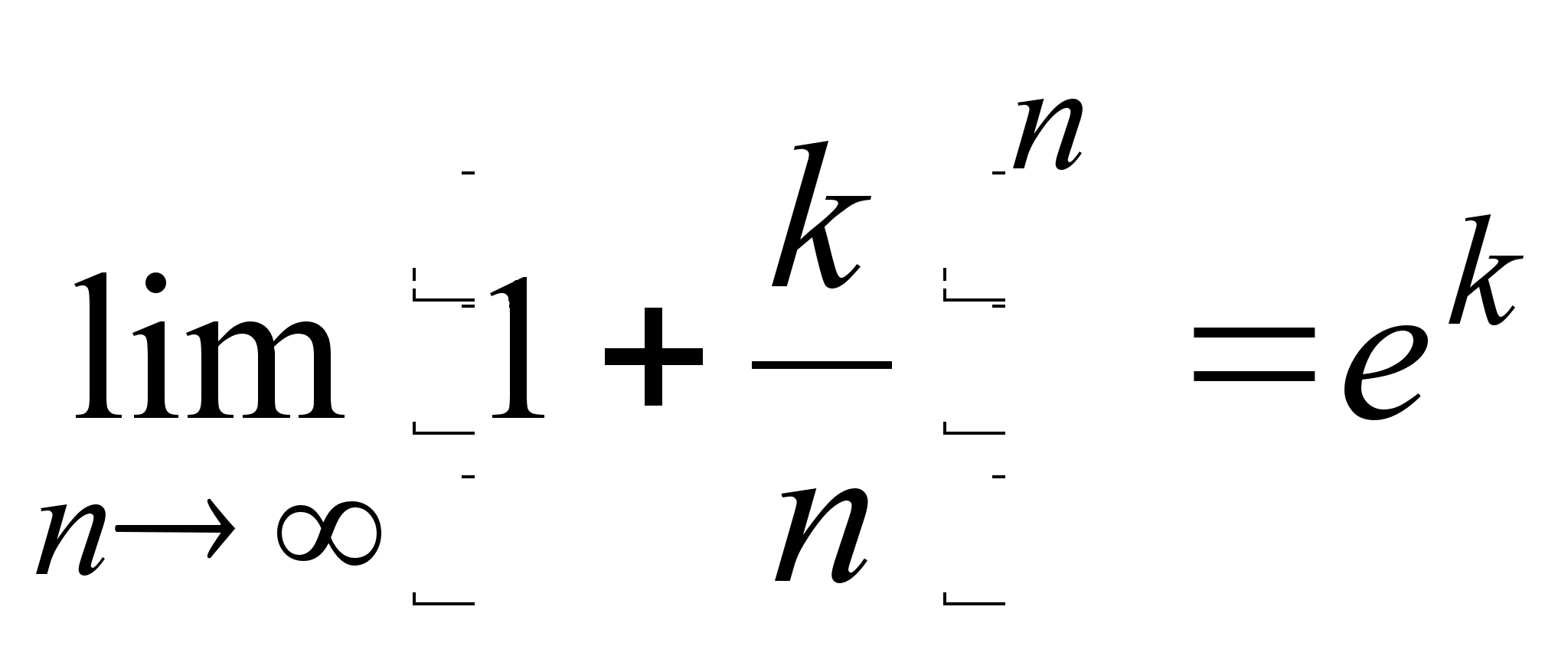 ,
,
справедливую
для любой постоянной
![]() .
.
Приведем пример
экономической
задачи, в которой
возникает число
![]() .
Предположим,
что в банк помещена
сумма
.
Предположим,
что в банк помещена
сумма ![]() под
под ![]() годовых. Тогда
через год сумма
вклада составит
годовых. Тогда
через год сумма
вклада составит
![]()
![]() ,
,
где
введено обозначение
![]() .
.
Предположим,
что вклад можно
снять по истечении
любого срока
в течение года,
и начисление
на вклад пропорционально
этому сроку,
т.е. за полгода
будет начислено
![]() ,
за месяц -
,
за месяц - ![]() ,
за один день
-
,
за один день
- ![]() .
Тогда к концу
года можно
получить доход
больший, чем
.
Тогда к концу
года можно
получить доход
больший, чем
![]() ,
действуя следующим
образом. Если,
например, в
середине года
закрыть счет
и полученную
сумму
,
действуя следующим
образом. Если,
например, в
середине года
закрыть счет
и полученную
сумму ![]() снова положить
в банк на оставшиеся
полгода, то в
конце года
сумма вклада
составит
снова положить
в банк на оставшиеся
полгода, то в
конце года
сумма вклада
составит
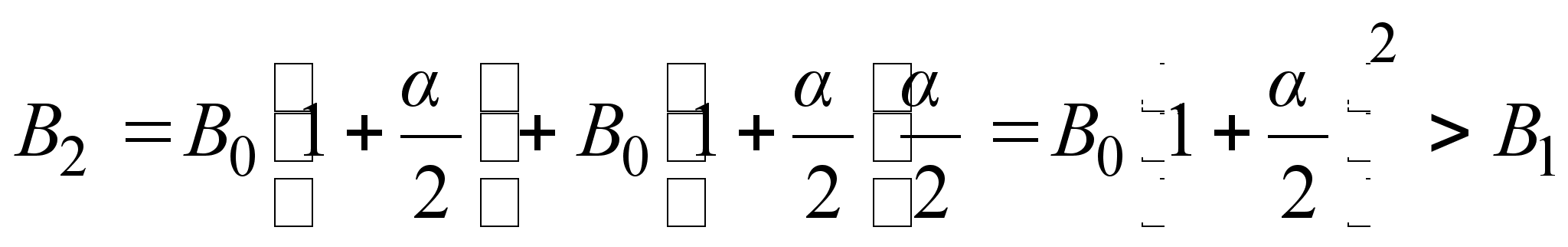 .
.
Если
повторять
операцию
закрытия-открытия
счета чаще,
например, каждый
месяц, то к концу
года будем
иметь 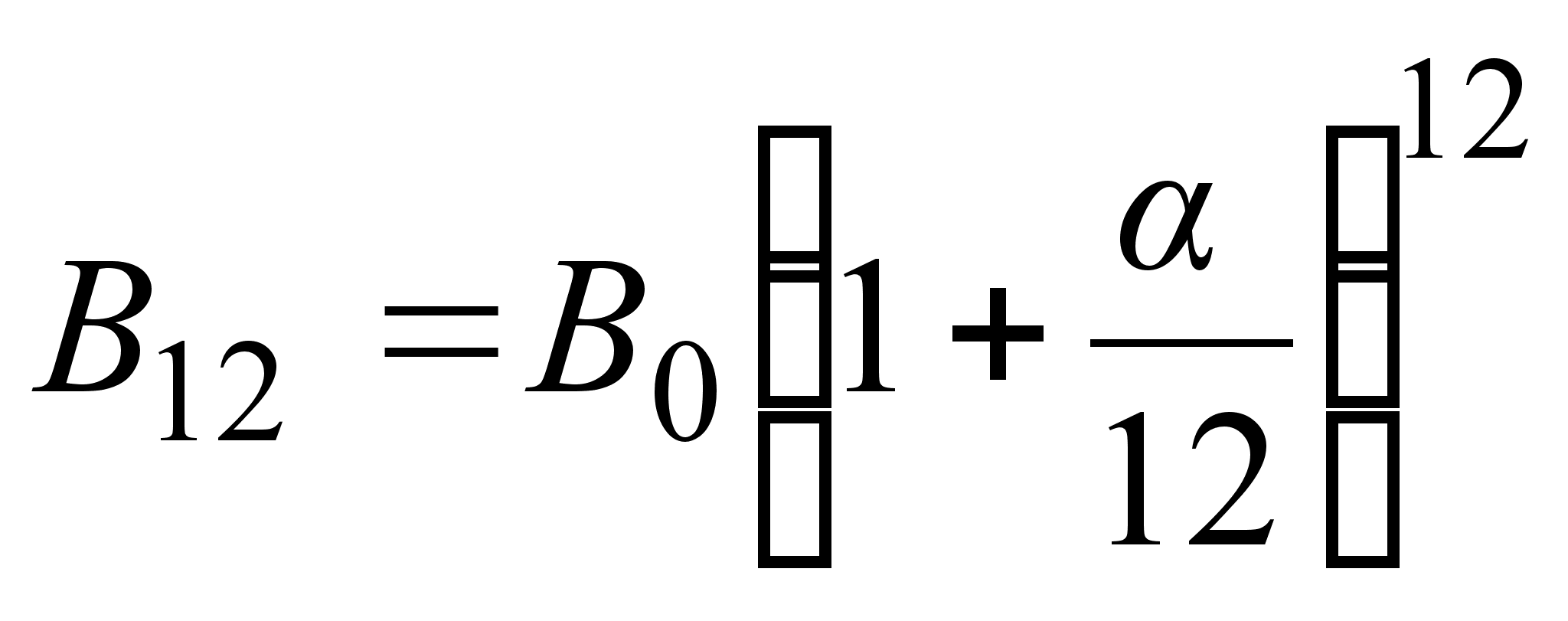 ,
а если каждый
день, то
,
а если каждый
день, то 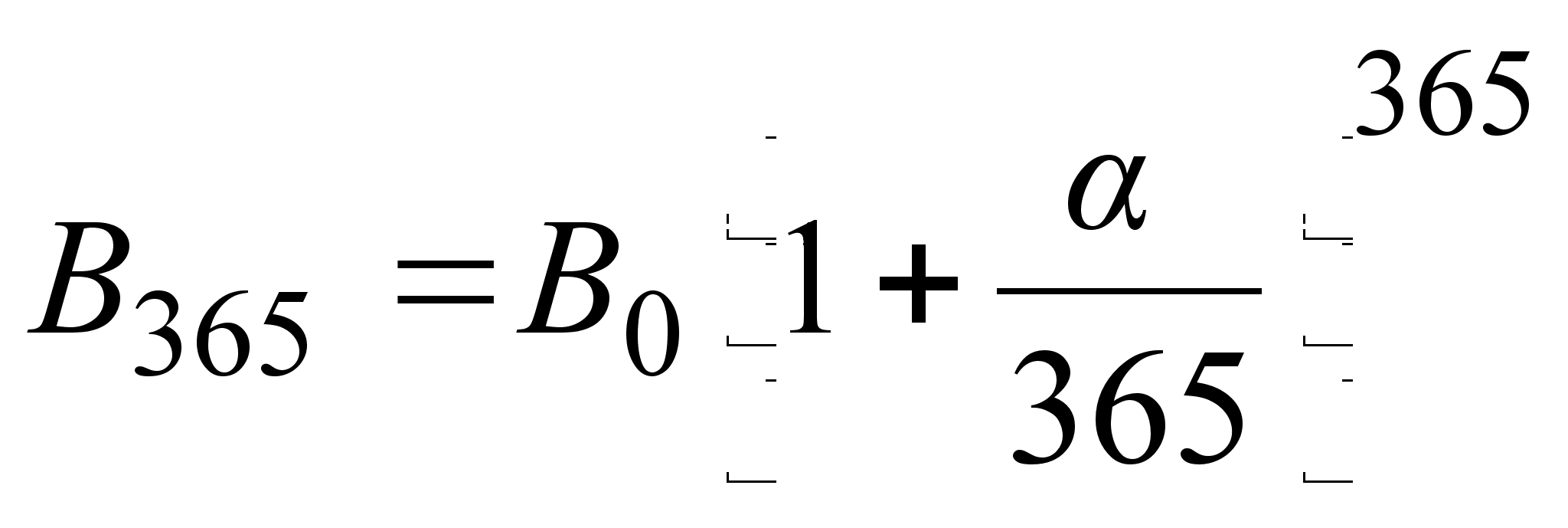 .
Если предположить,
что операция
закрытия-открытия
счета производится
.
Если предположить,
что операция
закрытия-открытия
счета производится
![]() раз в году через
равные промежутки
времени, то в
конце года
сумма вклада
составит
раз в году через
равные промежутки
времени, то в
конце года
сумма вклада
составит 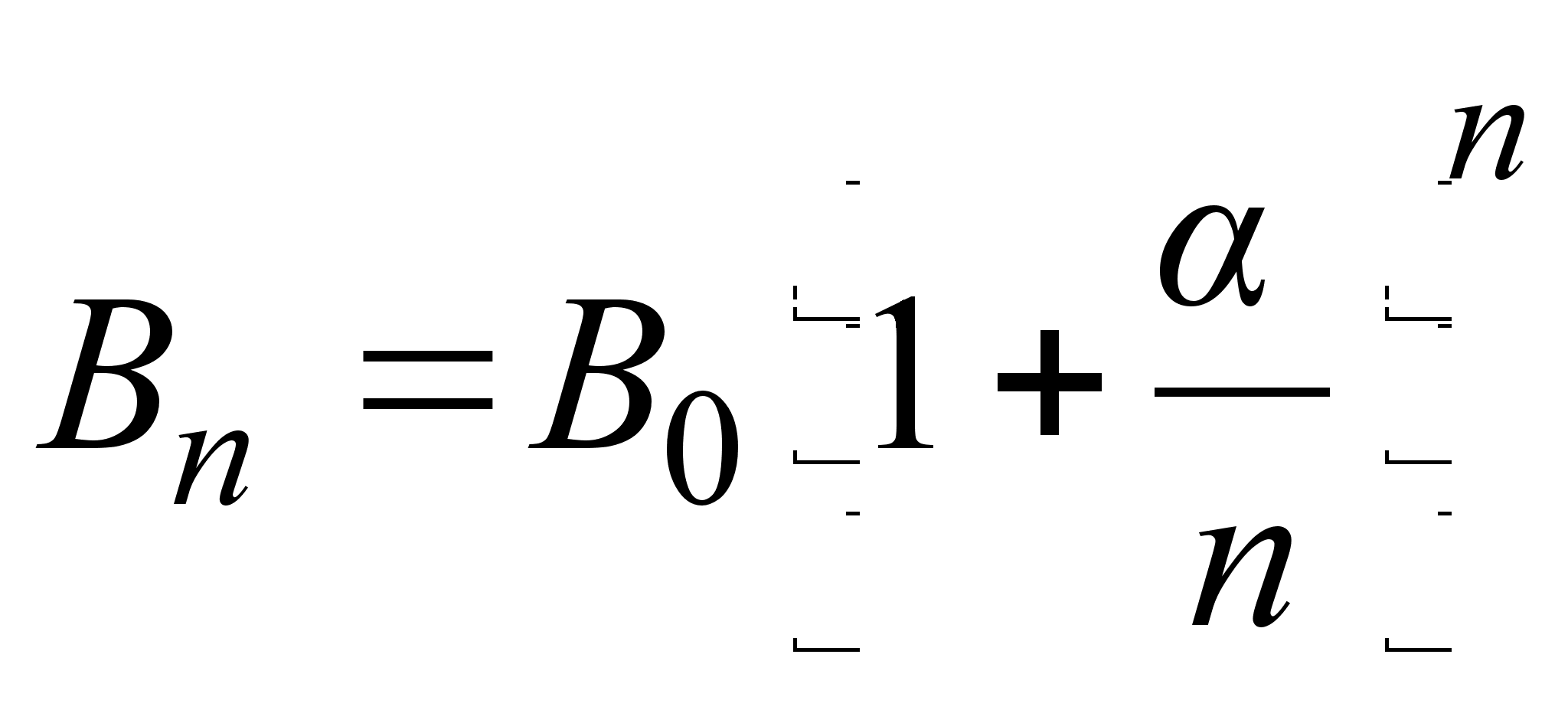 ,
а если представить,
что проценты
начисляются
непрерывно
(число операций
закрытия-открытия
счета неограниченно
растет), то
,
а если представить,
что проценты
начисляются
непрерывно
(число операций
закрытия-открытия
счета неограниченно
растет), то
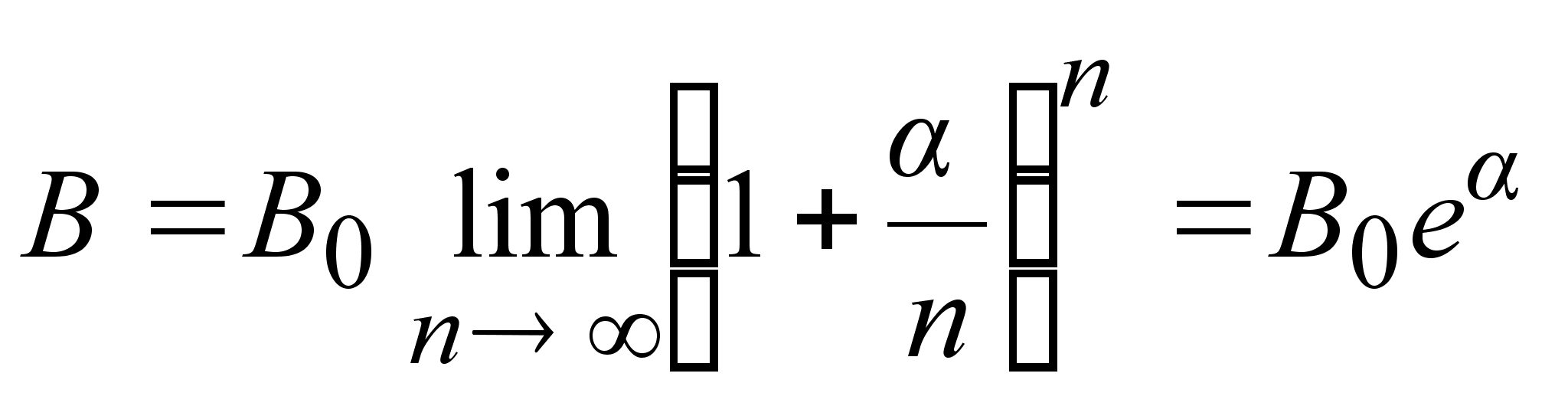 .
.
Таким образом,
максимальное
число процентов,
на которое
гипотетически
может увеличиться
вклад при данной
схеме начисления,
составляет
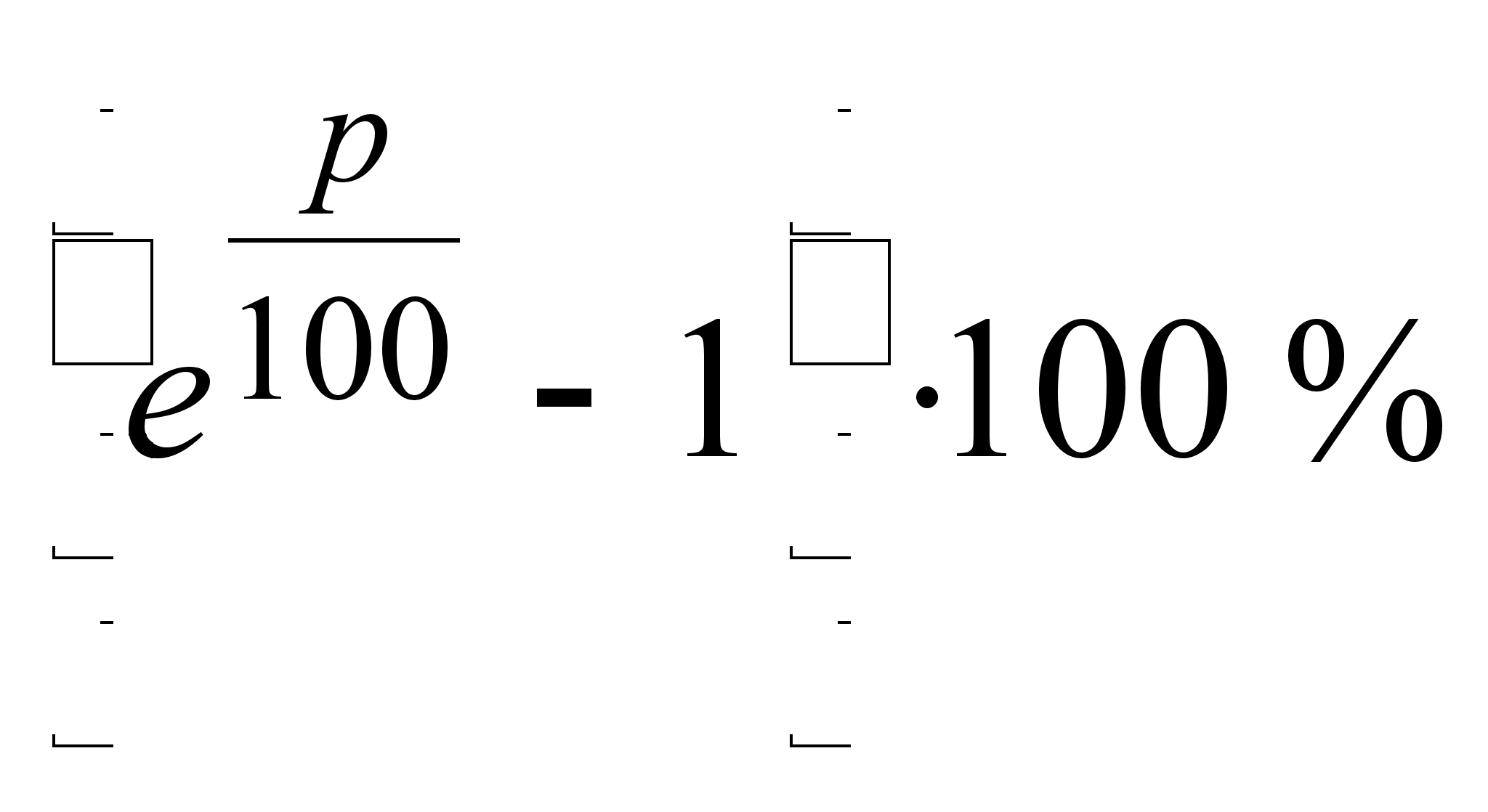 .
Например, при
номинальной
ставке 100 % (
.
Например, при
номинальной
ставке 100 % (![]() максимальная
эффективная
ставка составит
максимальная
эффективная
ставка составит ![]() .
.
Предел функции
Пусть функция ![]() определена
на некотором
интервале
определена
на некотором
интервале ![]() ,
содержащем
точку
,
содержащем
точку ![]() ,
за исключением
быть может
самой этой
точки. В дальнейшем
любой интервал,
содержащий
некоторую точку
,
за исключением
быть может
самой этой
точки. В дальнейшем
любой интервал,
содержащий
некоторую точку
![]() ,
будем называть
окрестностью
данной точки.
,
будем называть
окрестностью
данной точки.
Число ![]() называется
пределом функции
называется
пределом функции
![]() в точке
в точке ![]() ,
если для любой
последовательности
,
если для любой
последовательности
![]() ,
,
![]() ,
сходящейся
к
,
сходящейся
к ![]() ,
последовательность
значений функции
,
последовательность
значений функции
![]() сходится к
сходится к ![]() .
Обозначения:
.
Обозначения:
![]() или
или ![]() при
при ![]() .
.
При вычислении
пределов функций
используются
те же правила,
что и при вычислении
пределов
последовательностей.
В частности,
если существуют
пределы ![]() и
и ![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() ;
;
если, кроме
того, ![]() (тогда
(тогда ![]() для всех
для всех ![]() ,
достаточно
близких к
,
достаточно
близких к ![]() ),
то
),
то
![]() .
.
Примеры.
а) Найдем предел
функции ![]() в точке
в точке ![]() .
Для произвольной
последовательности
.
Для произвольной
последовательности
![]() такой, что
такой, что ![]() ,
,
![]() ,
на основании
свойств пределов
последовательностей
имеем
,
на основании
свойств пределов
последовательностей
имеем
![]() .
.
Отсюда по определению предела функции получаем
![]() .
.
б) Найдем предел
функции 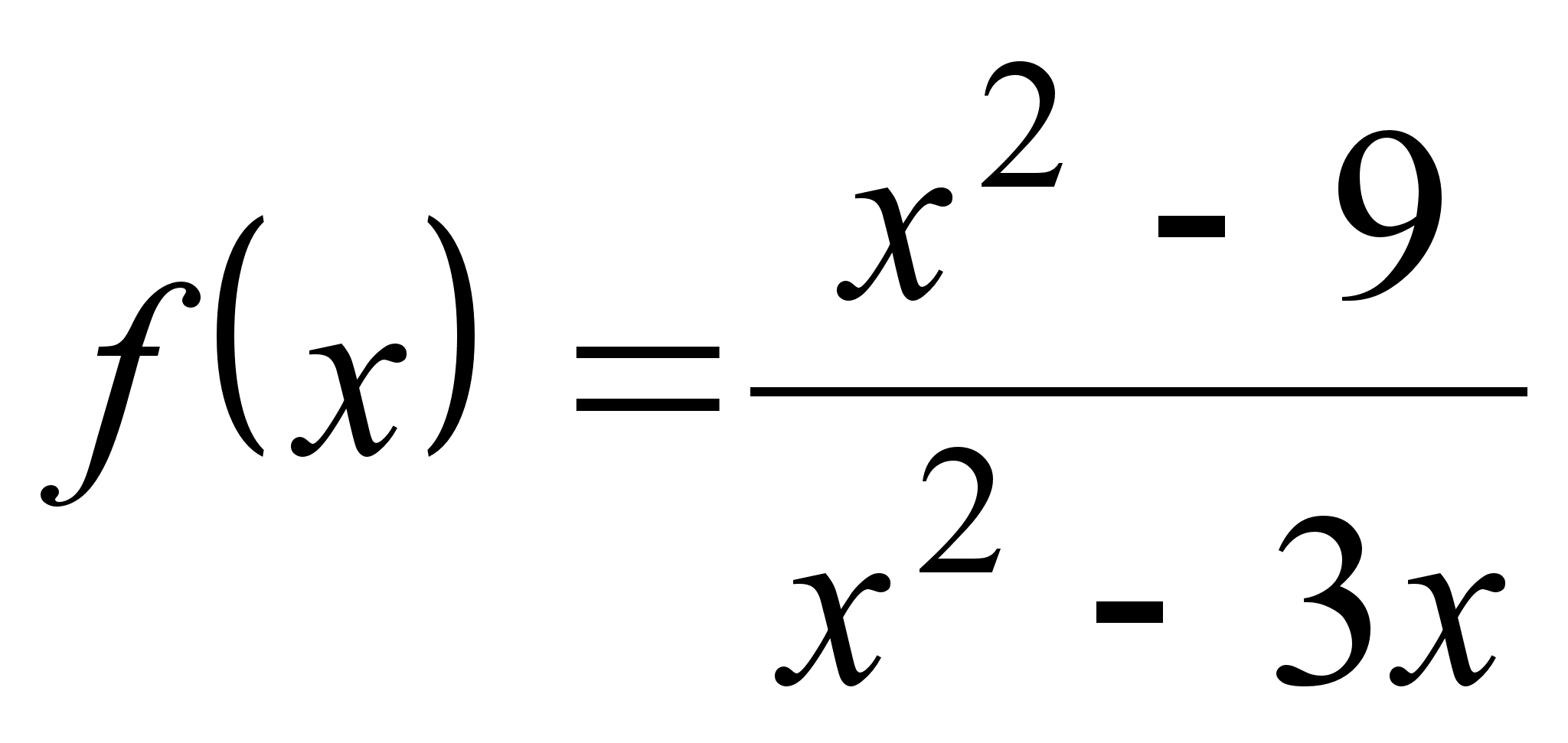 в точке
в точке ![]() ,
в которой функция
не определена.
Для произвольной
последовательности
,
в которой функция
не определена.
Для произвольной
последовательности
![]() такой, что
такой, что ![]() ,
,
![]() ,
имеем
,
имеем
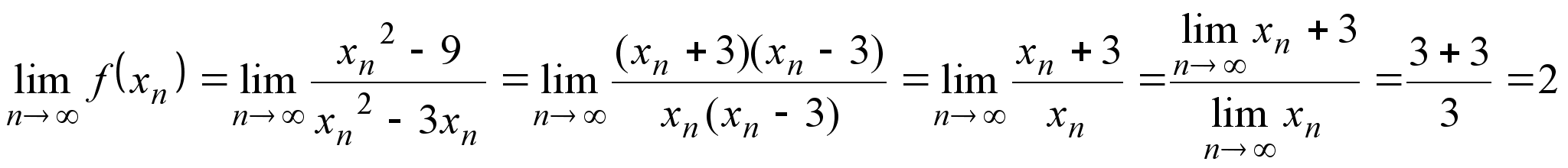 .
.
Отсюда получаем
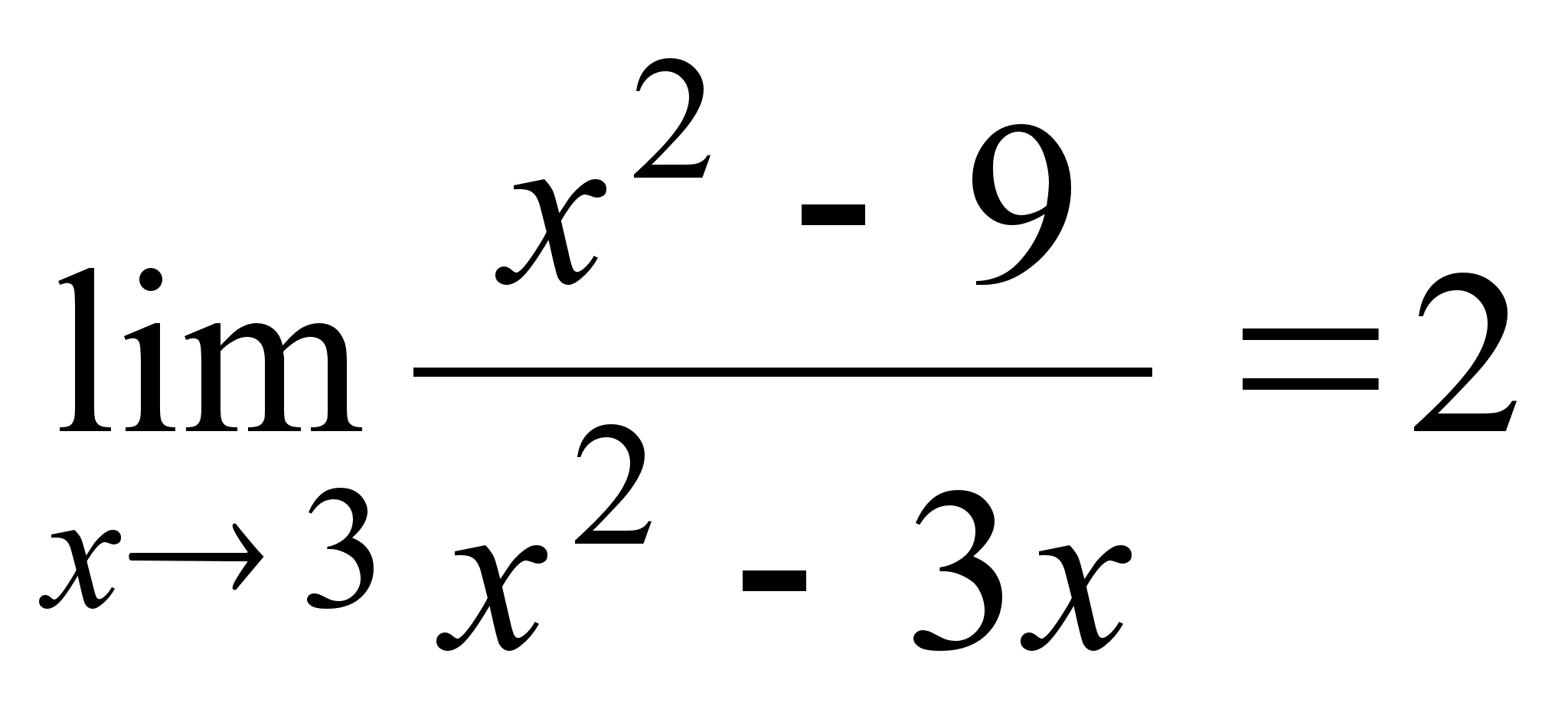 .
.
Пределы в бесконечности. Бесконечные пределы
Данное
выше определение
предела функции
можно распространить
на случаи, когда
![]() или
или ![]() (по отдельности
или вместе)
являются не
числами, а символами
(по отдельности
или вместе)
являются не
числами, а символами
![]() ,
,
![]() или
или ![]() .
Так, например,
запись
.
Так, например,
запись
![]() ,
,
где ![]() - число, означает,
что для любой
бесконечно
большой последовательности
- число, означает,
что для любой
бесконечно
большой последовательности
![]() ,
стремящейся
к
,
стремящейся
к ![]() ,
последовательность
,
последовательность
![]() сходится к
сходится к ![]() .
Аналогично,
запись
.
Аналогично,
запись
![]() ,
,
означает,
что для любой
последовательности
![]() ,
стремящейся
к
,
стремящейся
к ![]() ,
последовательность
,
последовательность
![]() стремится к
стремится к
![]() .
.
Примеры. а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) 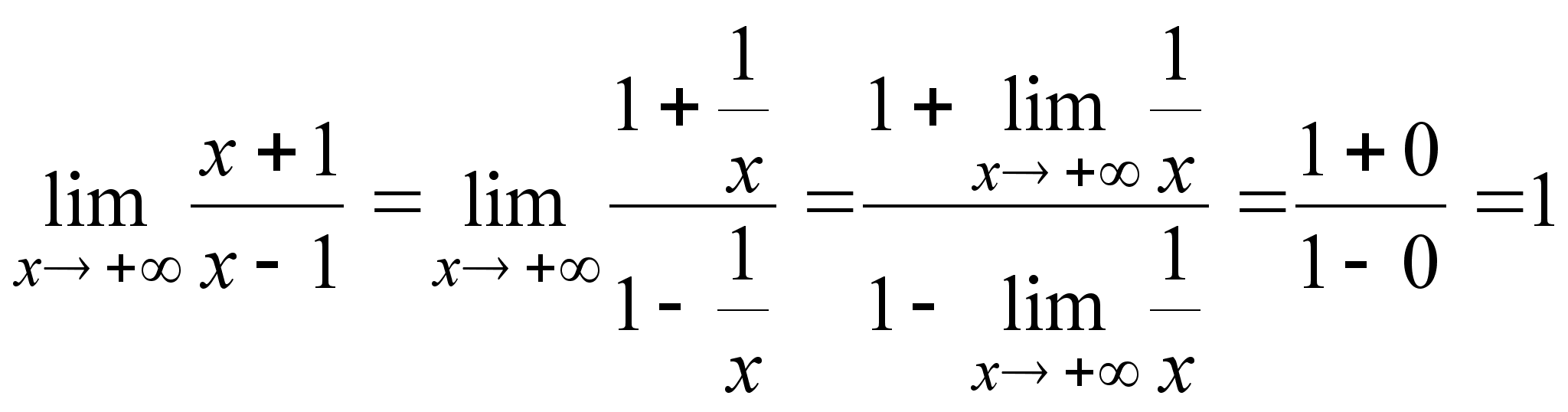 .
.
В качестве более сложного примера приведем равенство
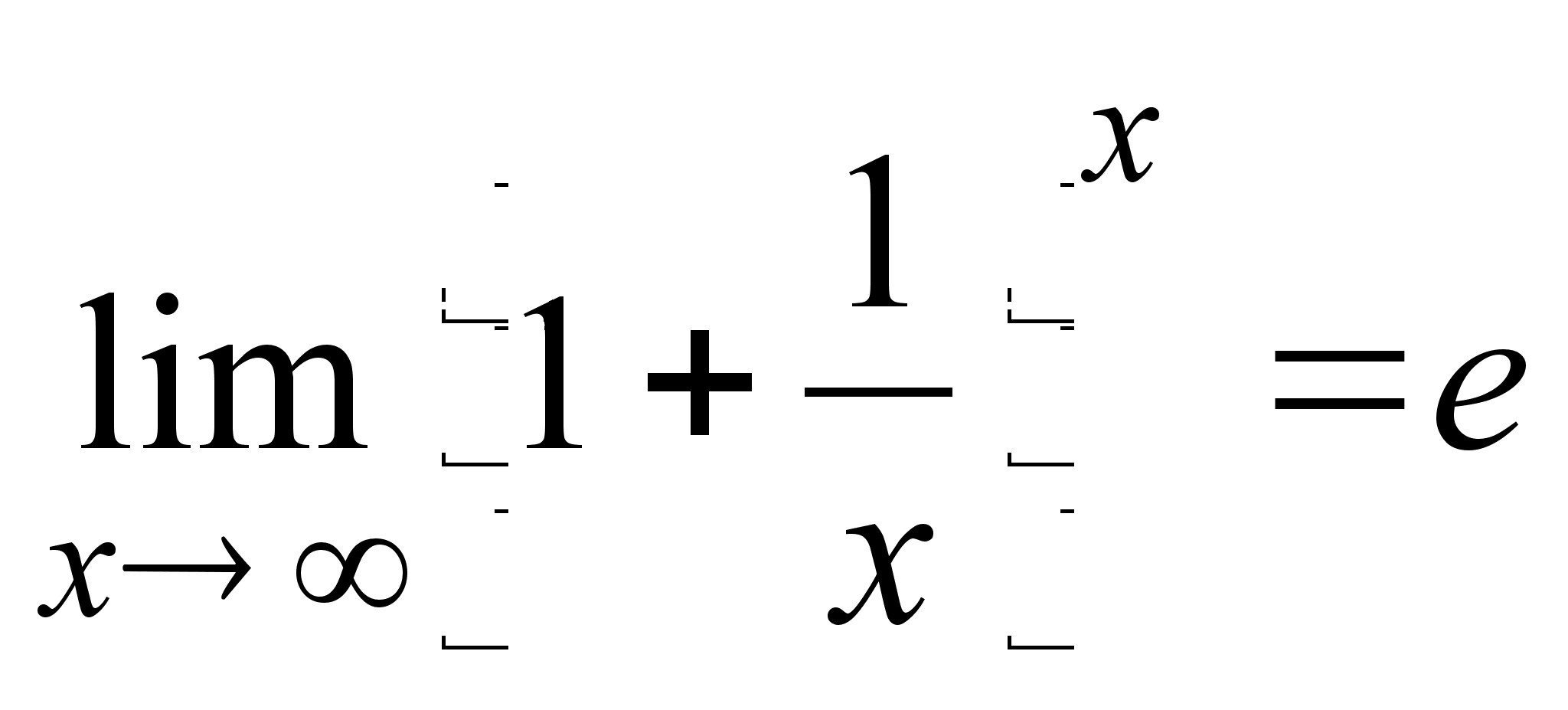 ,
,
которое
можно доказать,
исходя из определения
числа ![]() .
Заметим, что
этому равенству
можно придать
вид
.
Заметим, что
этому равенству
можно придать
вид
![]() .
.
Непрерывность функции
Функция ![]() ,
определенная
в некоторой
окрестности
точки
,
определенная
в некоторой
окрестности
точки ![]() ,
называется
непрерывной
в точке
,
называется
непрерывной
в точке ![]() ,
если
,
если
![]() .
.
Если
ввести обозначения
![]() и
и ![]() (
(![]() называется
приращением
аргумента,
а
называется
приращением
аргумента,
а ![]() - соответствующим
приращением
функции), то
определению
непрерывности
можно придать
вид
- соответствующим
приращением
функции), то
определению
непрерывности
можно придать
вид
![]() .
.
Таким образом, непрерывность означает, что малым приращениям аргумента соответствуют малые приращения функции.
Функция называется
непрерывной
на множестве
![]() ,
если она непрерывна
в каждой точке
этого множества.
Справедливо
следующее
утверждение:
все основные
элементарные
функции непрерывны
на своих областях
определения.
,
если она непрерывна
в каждой точке
этого множества.
Справедливо
следующее
утверждение:
все основные
элементарные
функции непрерывны
на своих областях
определения.
Примеры. Следующие функции непрерывны на указанных множествах:
а) функция ![]() непрерывна
на R;
непрерывна
на R;
б) функция ![]() непрерывна
на
непрерывна
на ![]() ;
;
в) функция ![]() непрерывна
для всех
непрерывна
для всех ![]() ;
;
г) функция 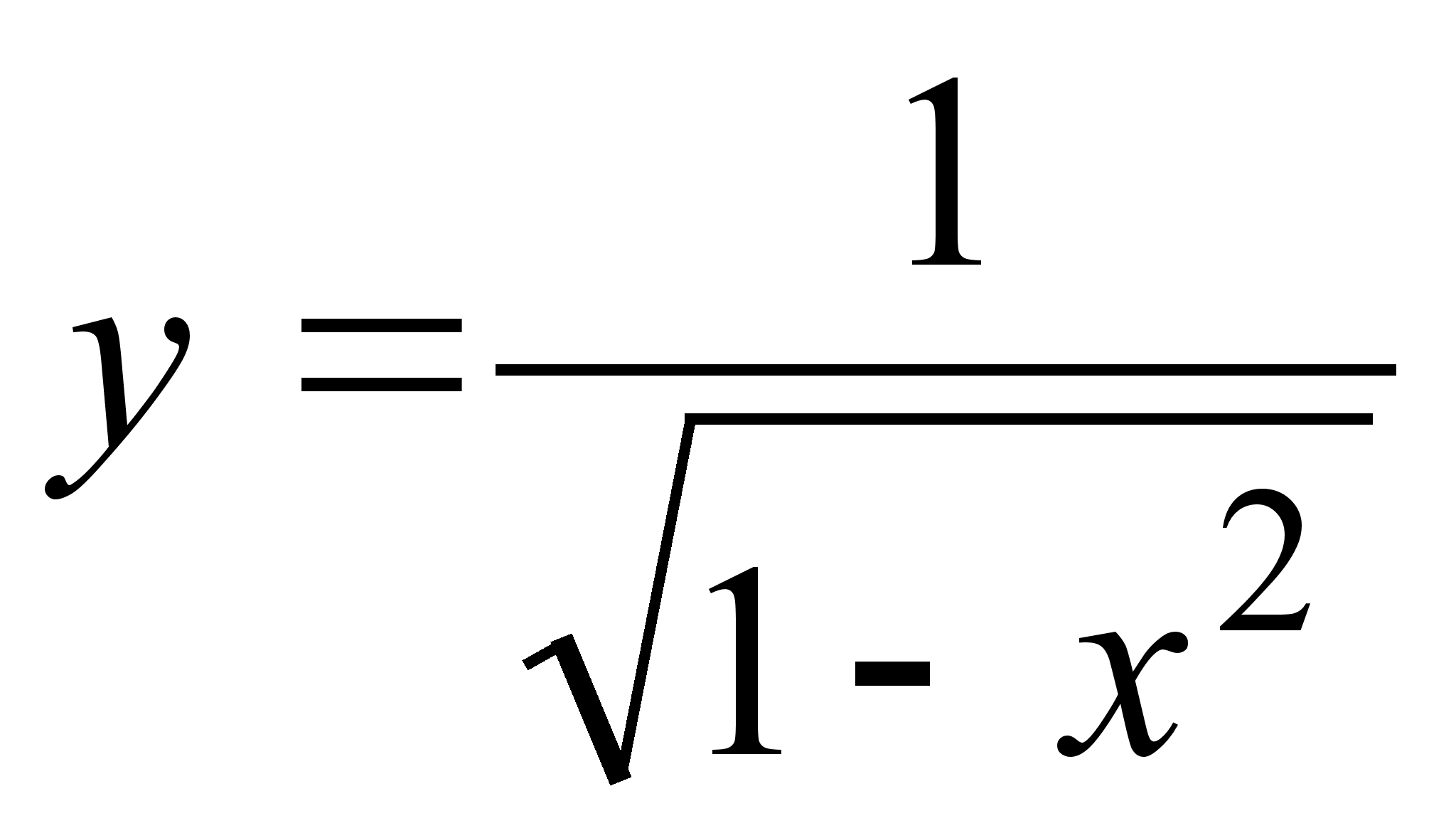 непрерывна
на
непрерывна
на ![]() .
.
Упражнения
1. Найти пределы последовательностей:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) 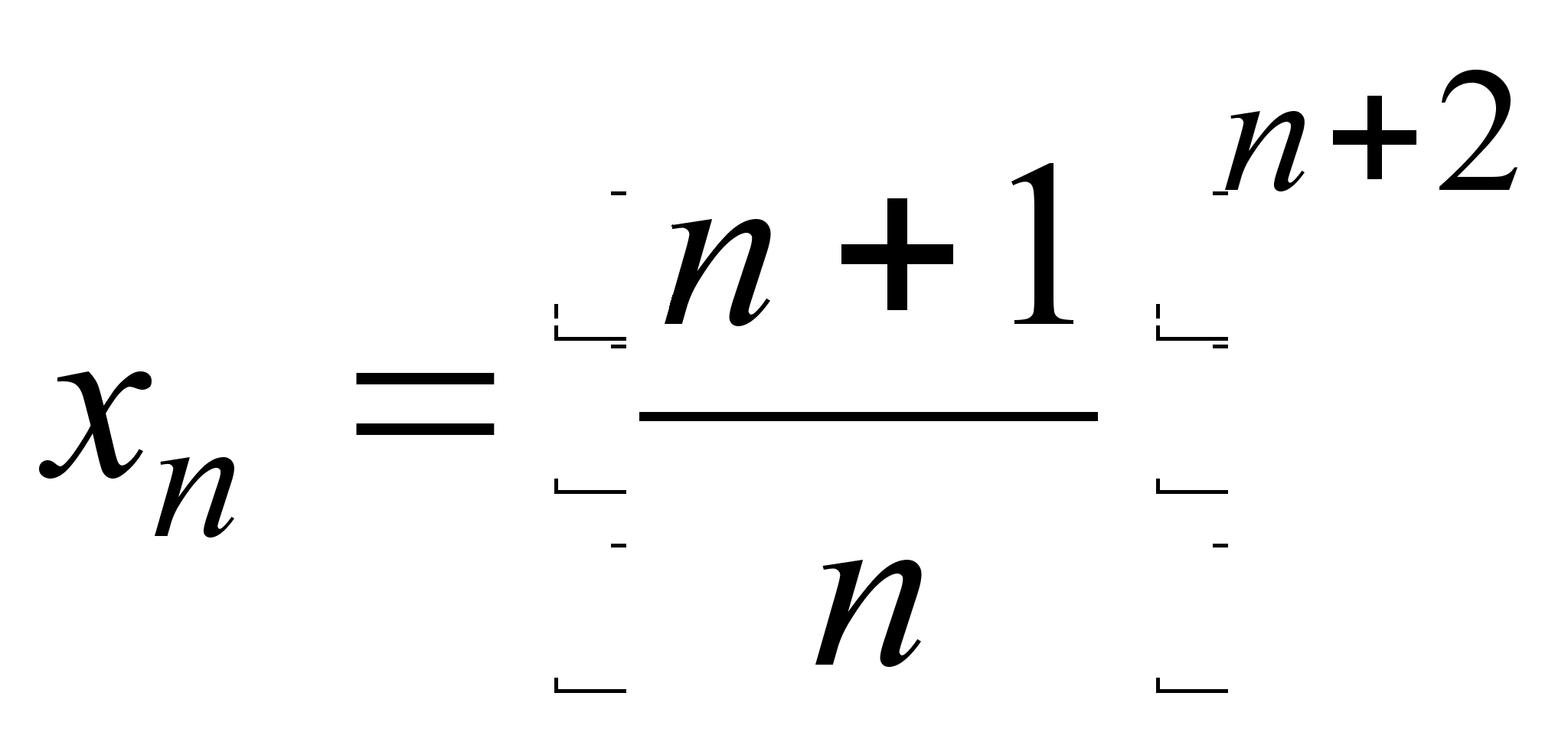 ;
;
18) 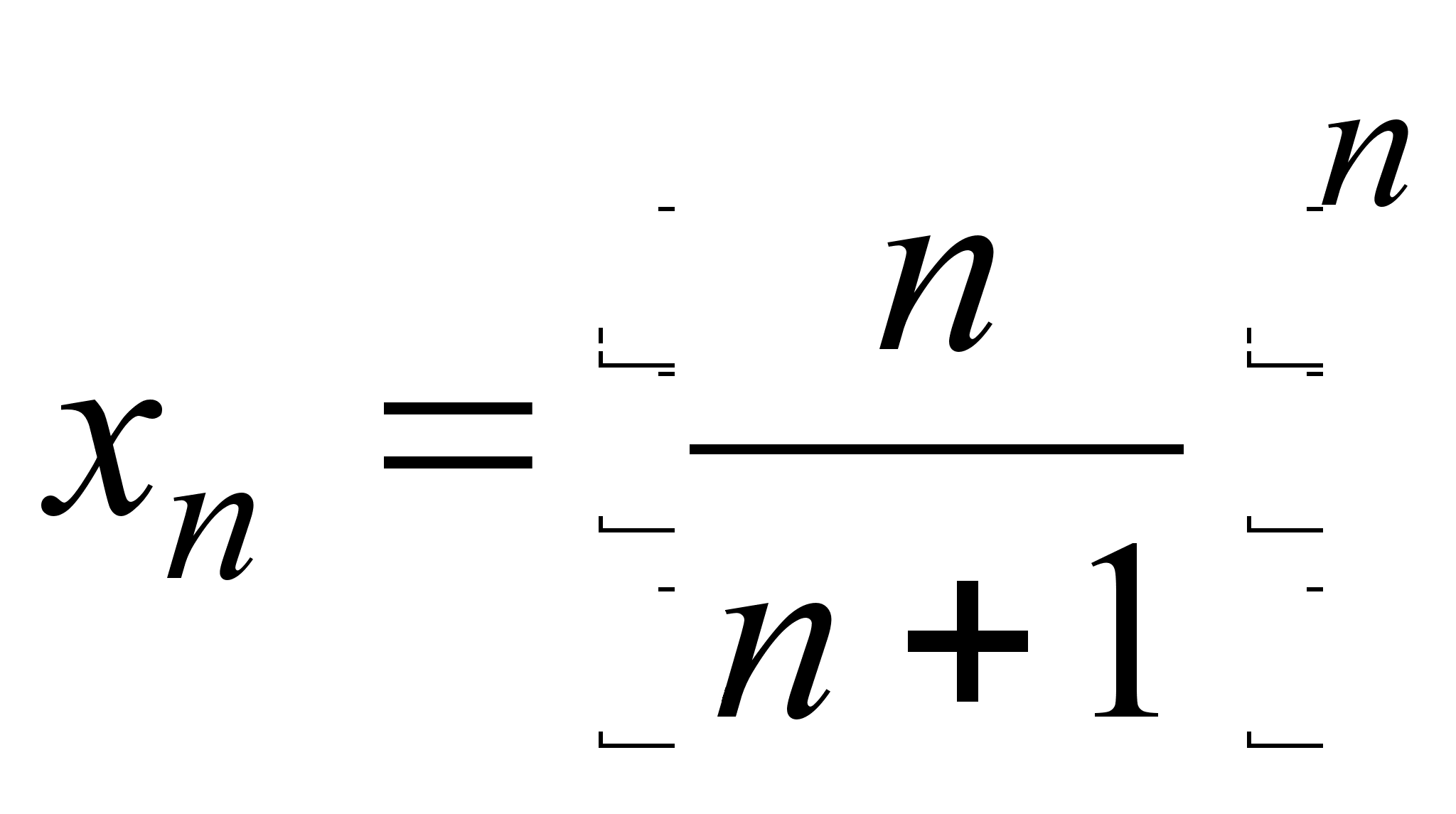 ;
;
19) 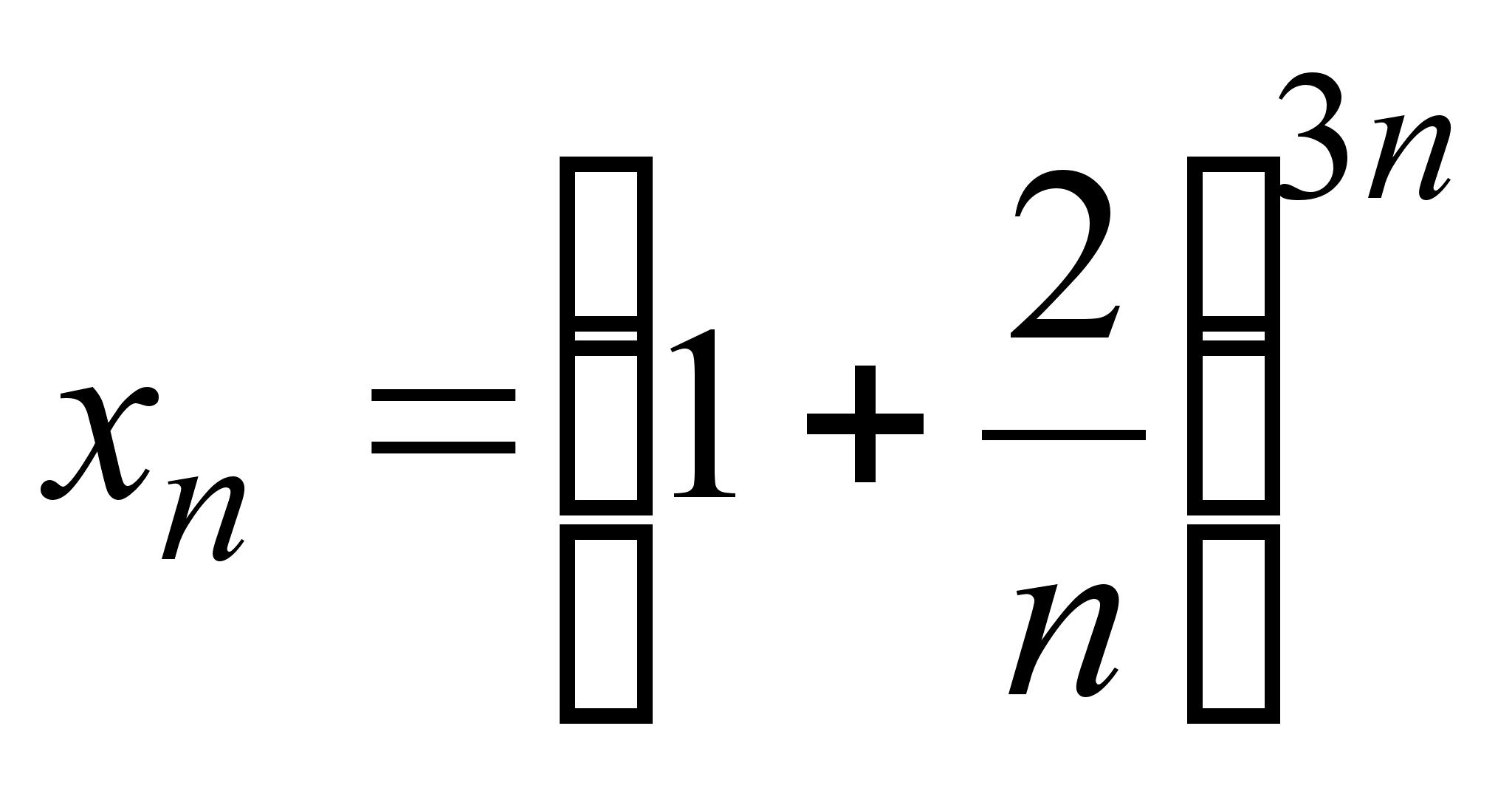 ;
;
20) 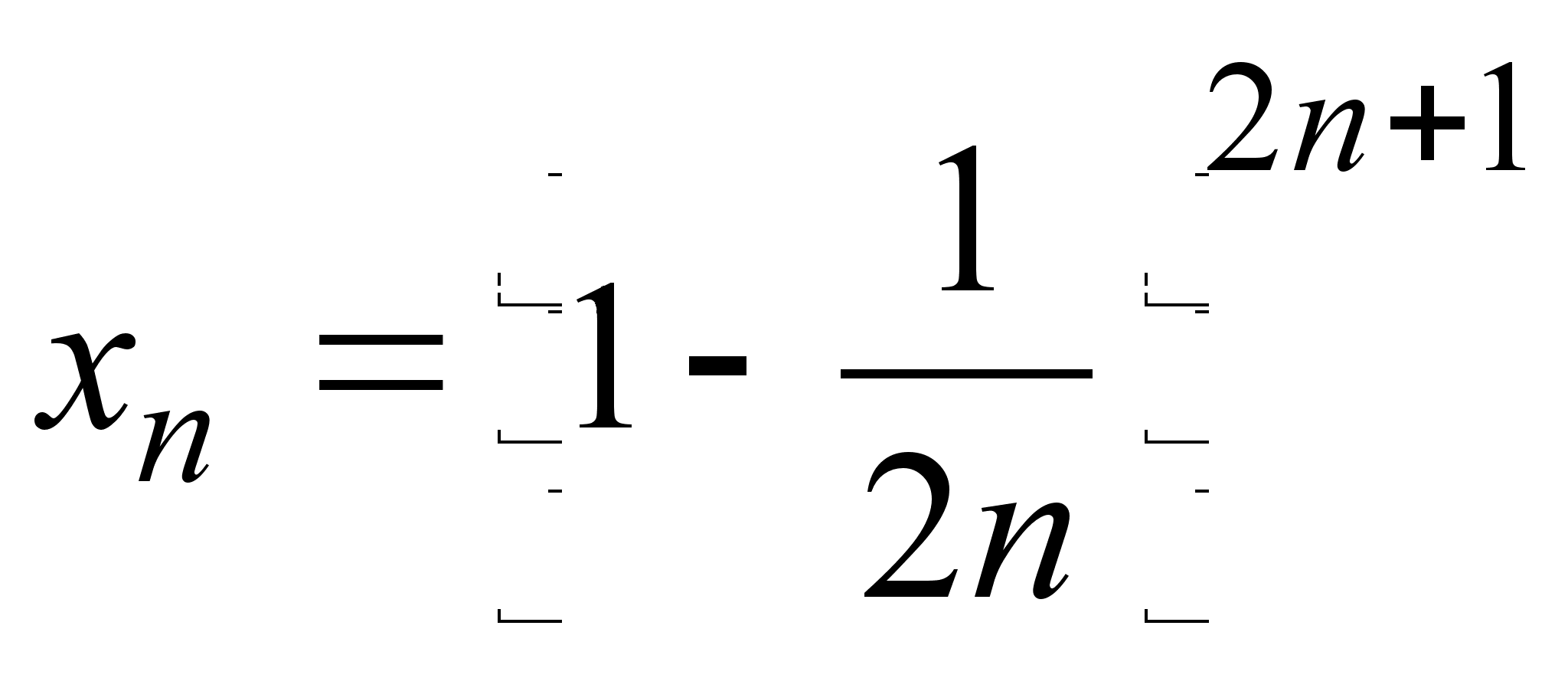 ;
;
21) ![]() ;
;
22) ![]() ;
;
23) ![]() ;
;
24) ![]() .
.
2. Найти пределы функций:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) 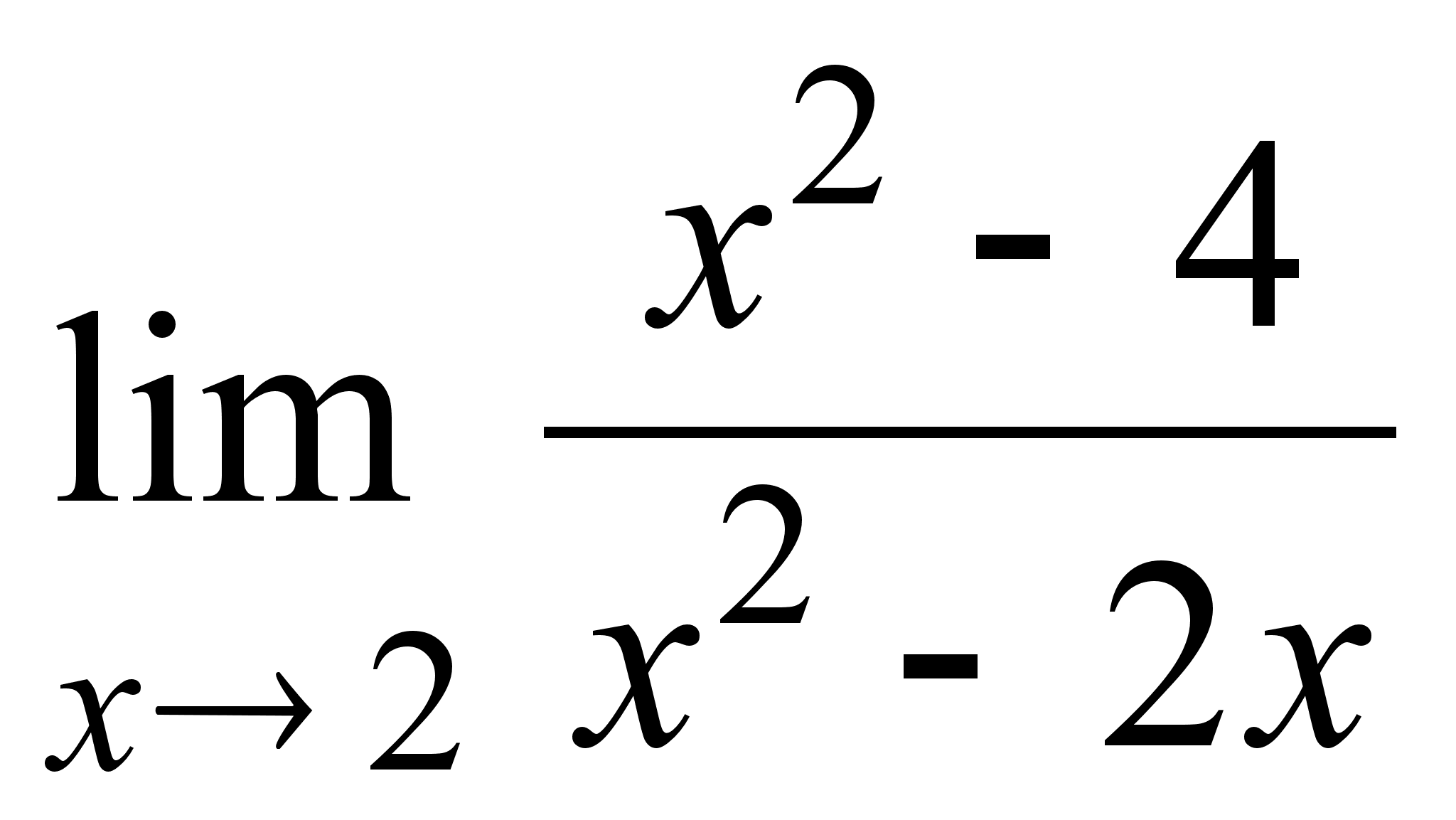 ;
;
5) ![]() ;
;
6) ![]() ;
;
7) 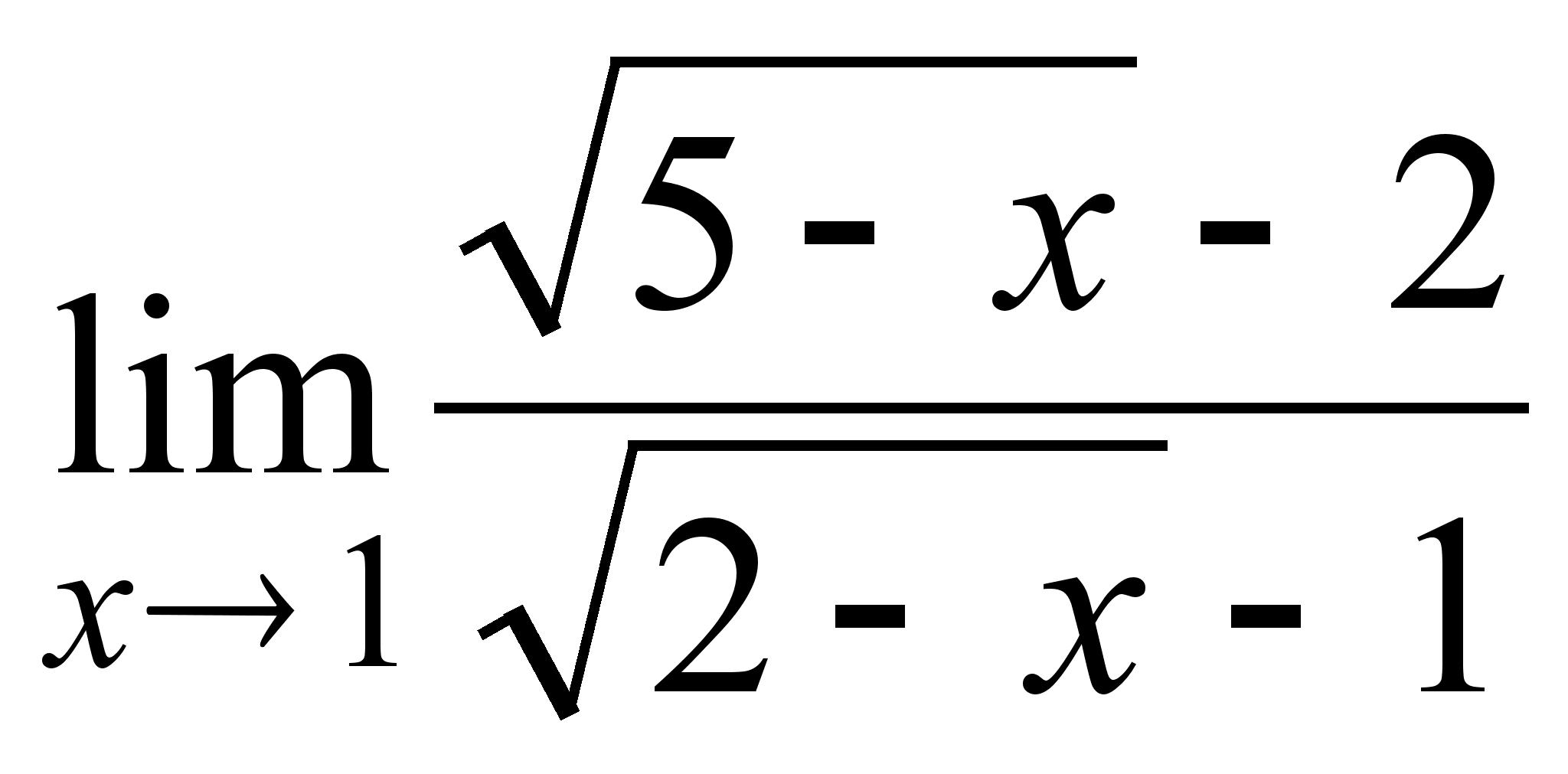 ;
;
8) 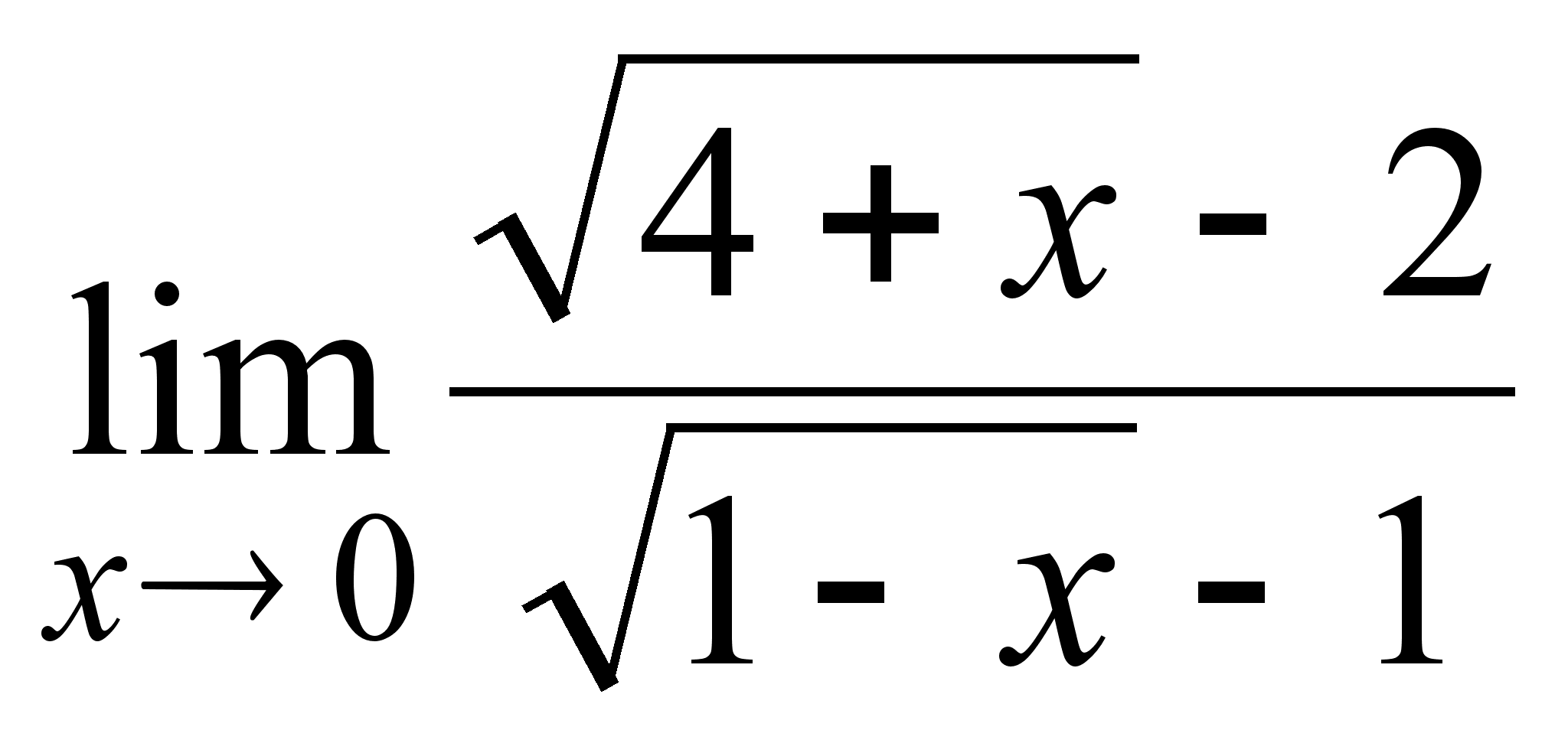 ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) 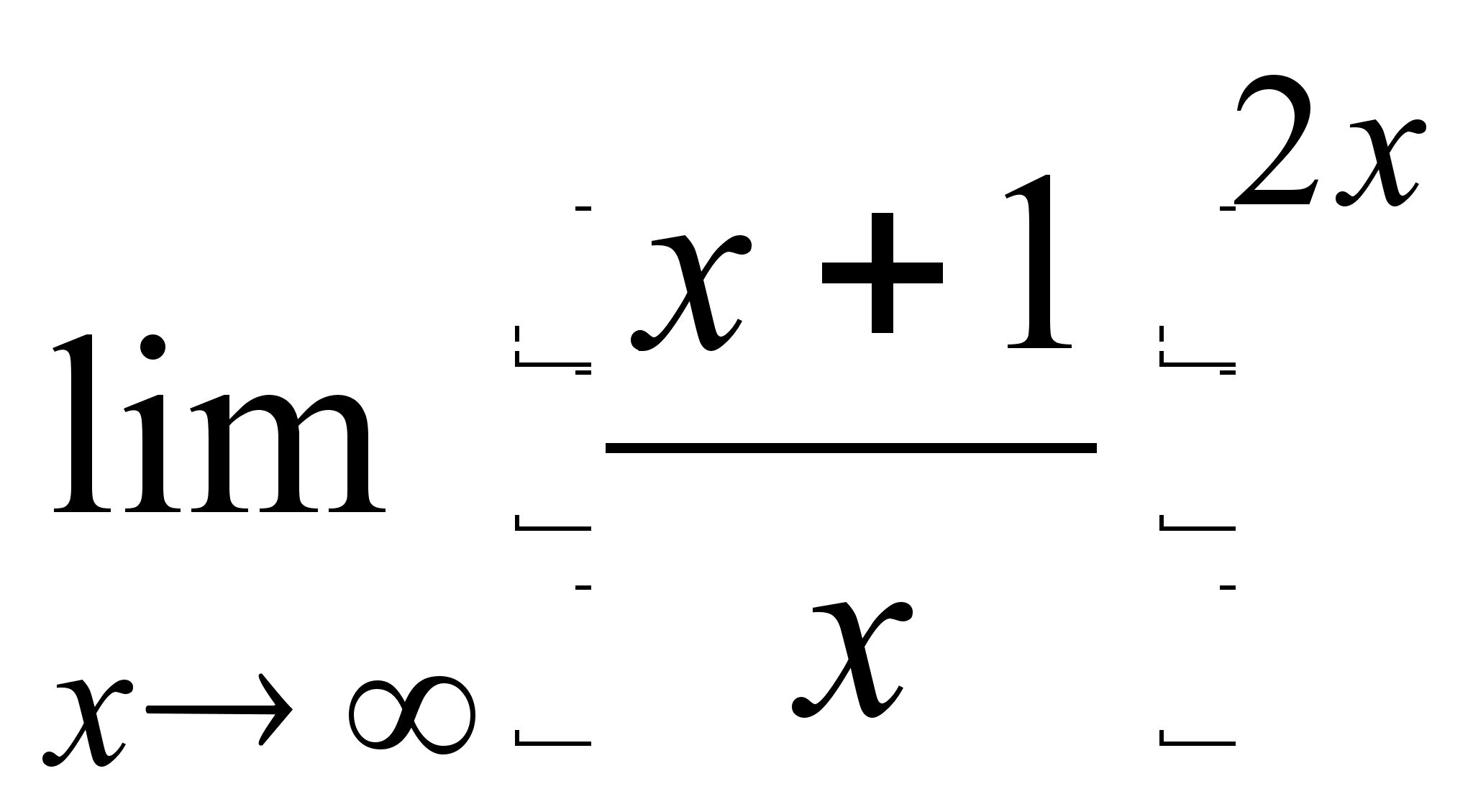 ;
;
18) 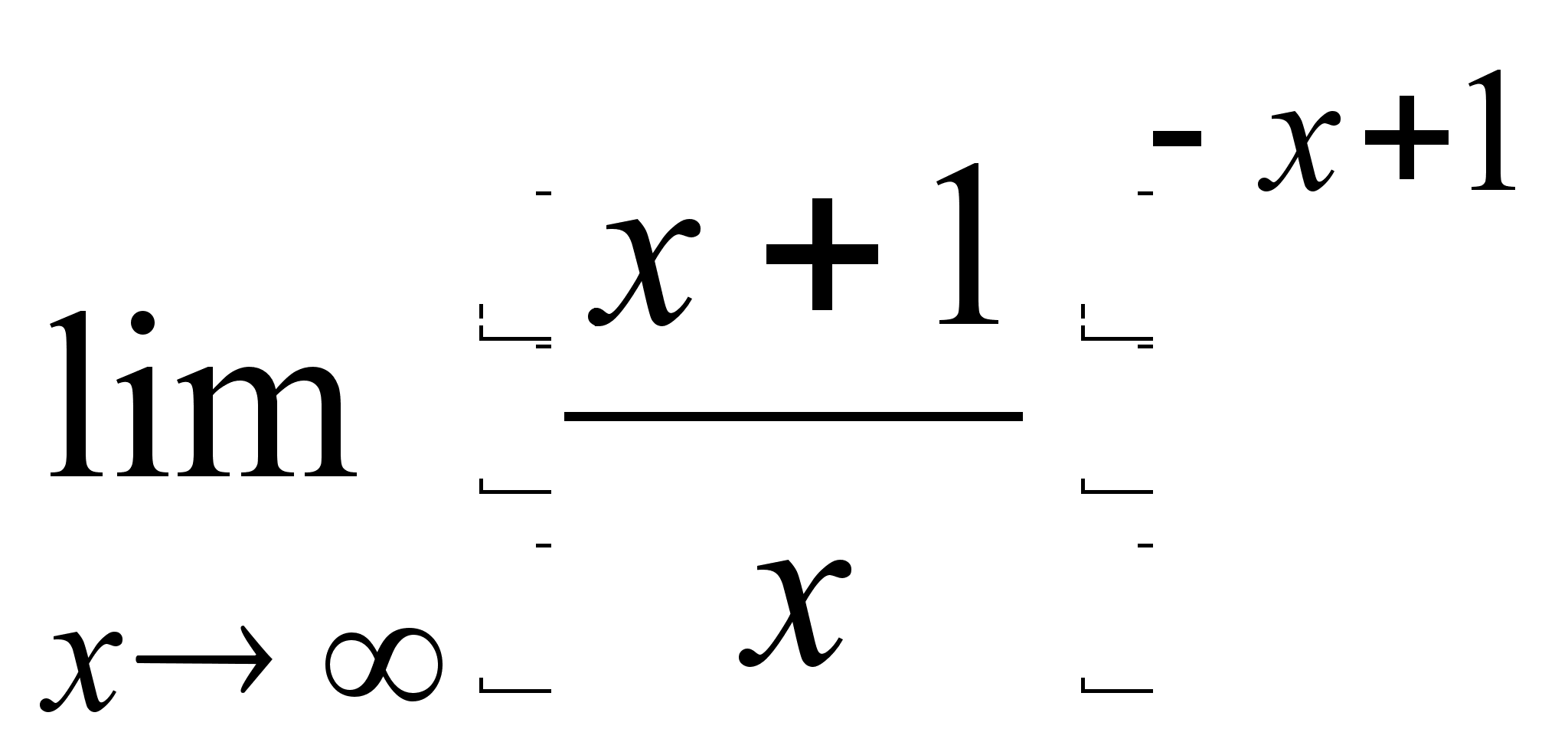 ;
;
19) 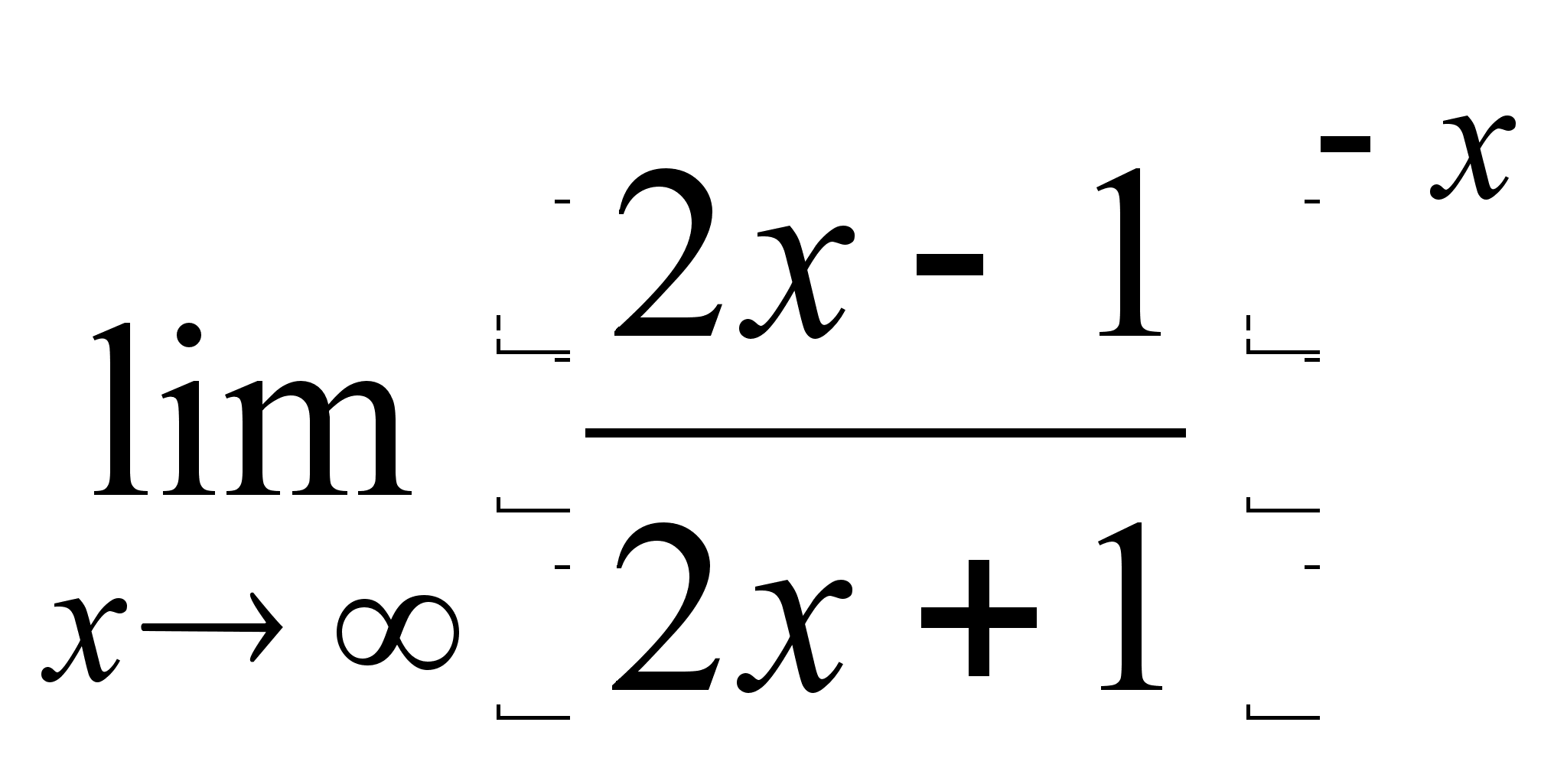 ;
;
20) 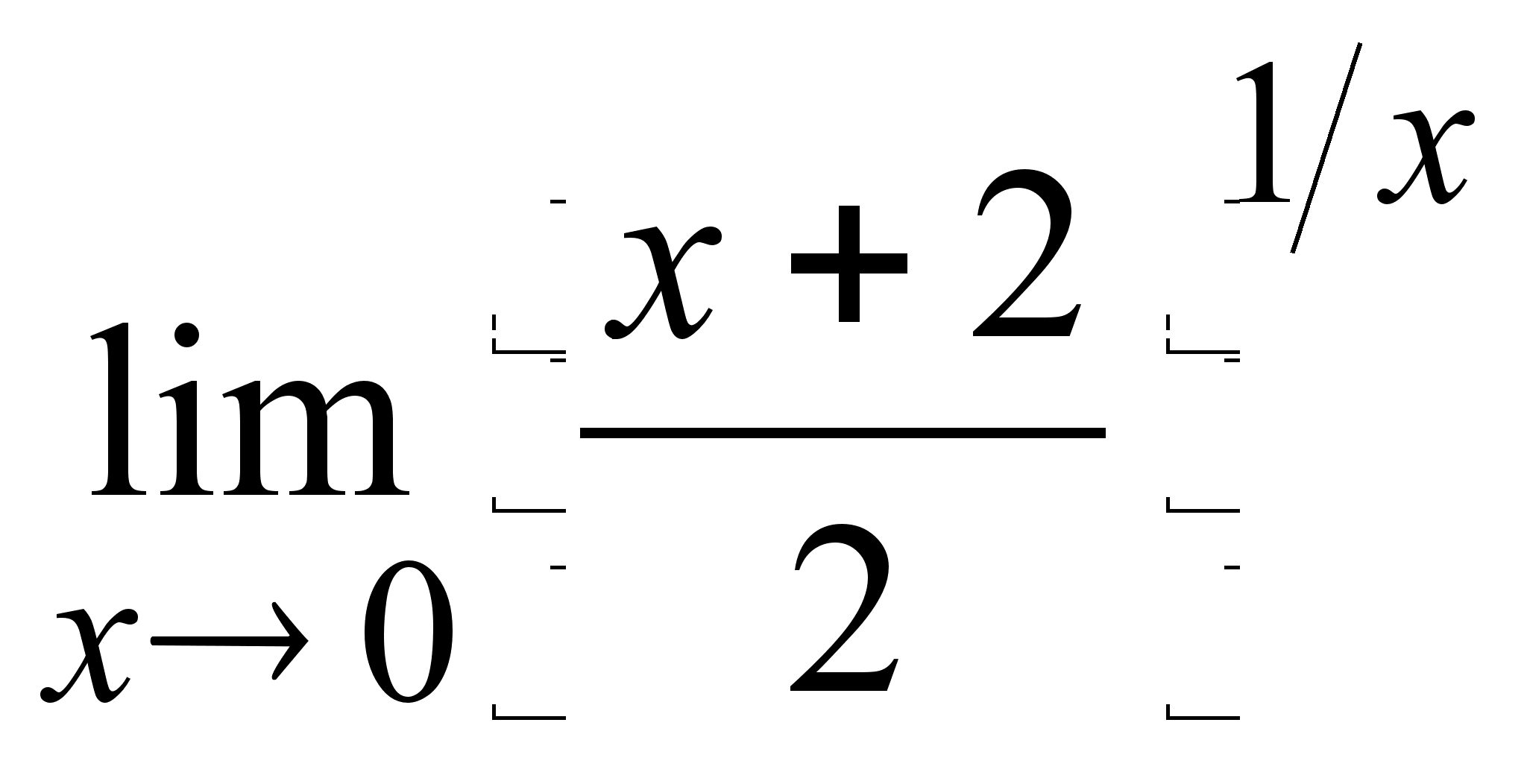
Ответы и указания к решению
1.
1) 0;
2) 0;
3) 1;
4) ![]() ;
;
5) 0;
6) 0;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) 0;
14) ![]() ;
;
15) 0;
16) ![]() ;
;
17) ![]() ; представить
; представить ![]() в виде произведения
в виде произведения 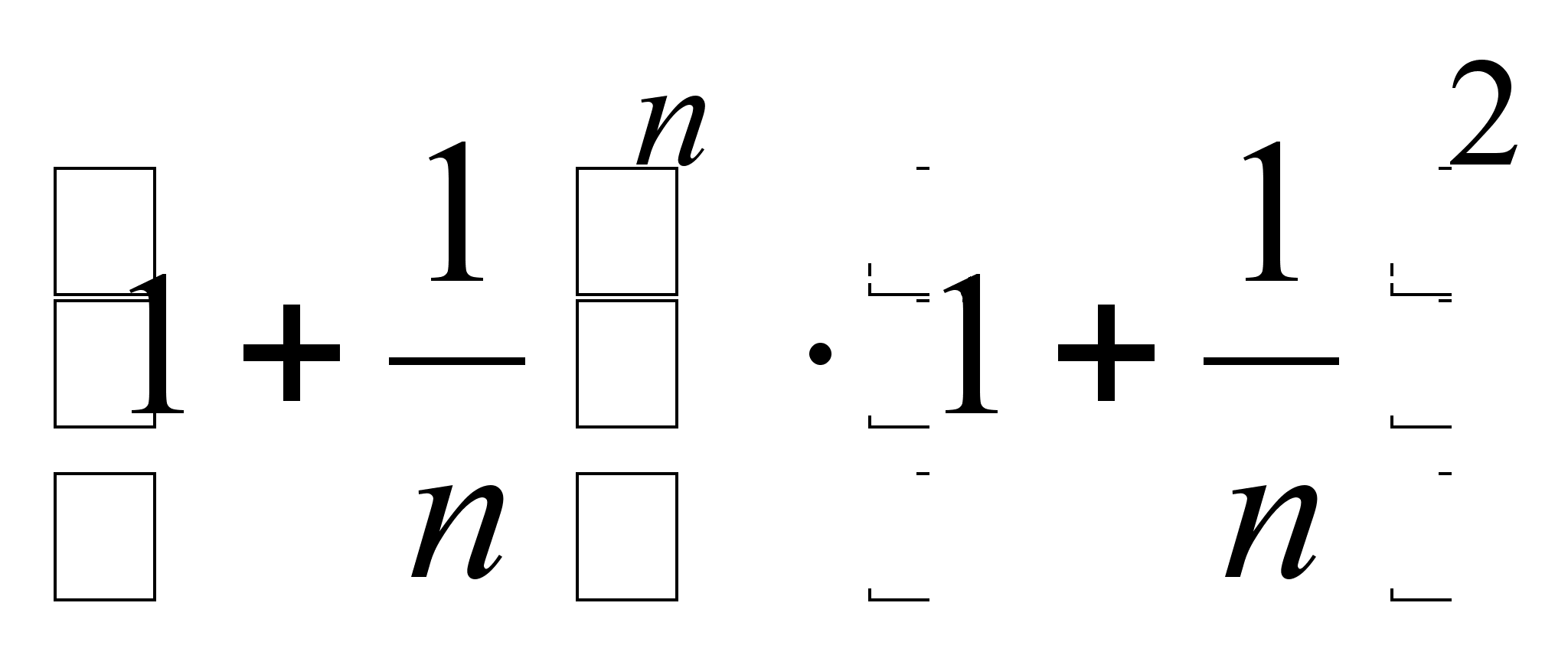 ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() ;
;
21) 0; преобразовать ![]() к виду
к виду ![]() ;
;
22) 0;
23) ![]() ;
;
24) ![]() .
.
2.
1) 2;
2) 1;
3) 2;
4) 2;
5) 3;
6) 4;
7) ![]() ;
;
8) ![]() ;
;
9) 2;
10) 0;
11) ![]() ;
;
12) ![]() ;
;
13)![]() ;
;
14) ![]() ;
;
15) 0;
16) 2;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() .
.
§ 3. Производная и ее применение
Производная характеризует скорость изменения функции при изменении ее аргумента. Она является основным инструментом исследования функций в математическом анализе, в частности, используется для отыскания точек экстремума: в этих точках производная либо равна нулю, либо не существует. Через производную определяется понятие эластичности функции, применяемое в экономических приложениях.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
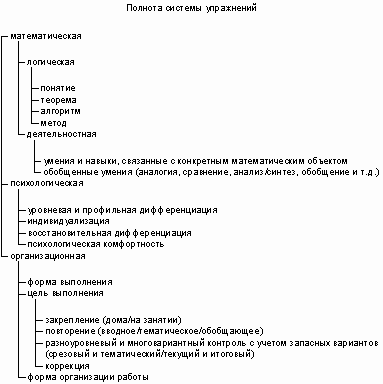
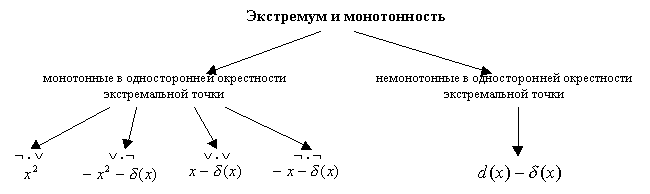
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
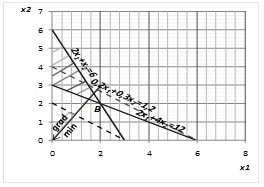
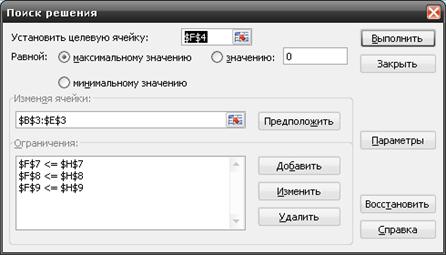
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





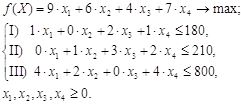
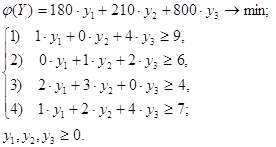
0 комментариев