Навигация
Геометрический и физический смысл производной
43586
знаков
0
таблиц
1328
изображений
2. Геометрический и физический смысл производной
а) Геометрический смысл производной. Рассмотрим график функции 
, дифференцируемой в точке 
(рис. 13). Проведем через точки 
и 
графика прямую 
, и пусть 
- угол ее наклона к оси 
. Тогда
. (1)
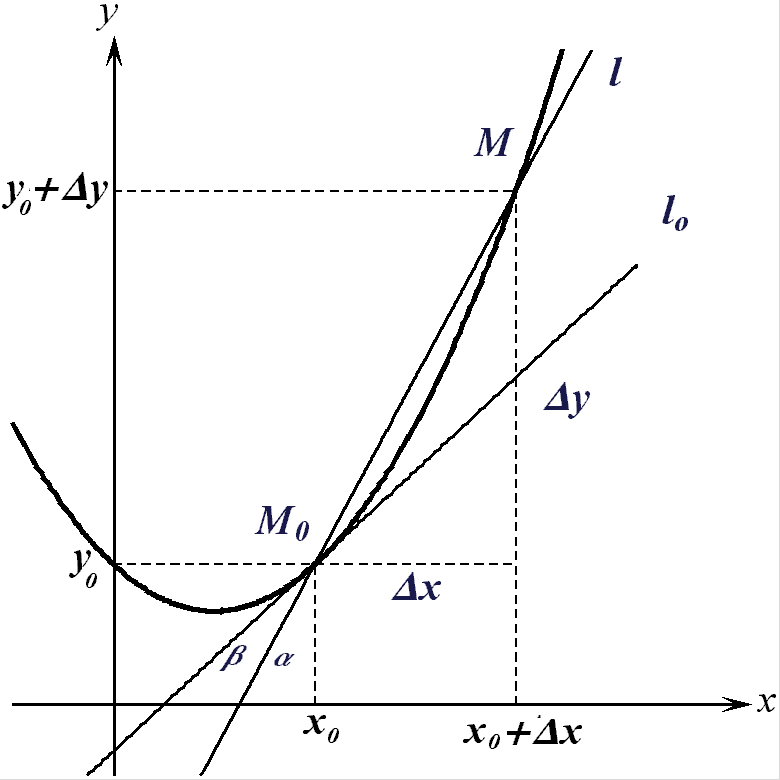
Рис. 13.
Если 
стремится к нулю, то 
также стремится к нулю, и точка 
приближается к точке 
, а прямая - к касательной 
, образующей с осью угол 
. При этом равенство (1) принимает вид:
, (2)
откуда следует, что производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке.
Пример. Найдем угол 
наклона касательной к графику функции 
в точке 
. Поскольку 
, то в силу формулы (2) получаем 
. Следовательно угол 
, то есть касательная параллельна оси 
.
б) Физический смысл производной. Если - время движения, а 
- путь, пройденный за это время, то отношение 
есть средняя скорость движения на отрезке 
, а 
- мгновенная скорость в момент времени 
.
3. Исследование функций с помощью производной
Функция 
называется возрастающей (убывающей) на интервале 
, если для любых 
из 
следует 
(
).
Интервалы возрастания или убывания могут быть найдены на основании следующего утверждения.
Теорема 1. Если 
для всех 
, то функция возрастает на интервале ; если 
для всех , то функция убывает на интервале .
Точка 
называется точкой локального максимума (минимума) функции , если для всех из некоторой окрестности точки , 
, выполнено неравенство 
(
). Точки максимума и минимума называются точками экстремума функции.
Для отыскания точек экстремума используются следующие теоремы.
Теорема 2 (необходимое условие экстремума). Если функция имеет экстремум в точке и дифференцируема в этой точке, то 
.
Из этой теоремы вытекает, что в точках экстремума функции производная либо равна нулю, либо не существует. Такие точки называются критическими. Экстремумы функции следует искать среди ее критических точек.
Теорема 3 (достаточное условие экстремума). Пусть 
- критическая точка функции 
. Если при переходе через точку производная 
меняет знак с "+" на "–", то в точке функция 
имеет максимум, а если с "–" на "+", то – минимум. Если производная не меняет знак при переходе через точку , то в этой точке экстремума нет.
Проводимый на основе сформулированных теорем анализ поведения функций используют при построении их графиков.
Примеры. а) Найдем интервалы возрастания и убывания функции
,
и ее экстремумы.
Производная рассматриваемой функции существует при любом и равна 
. Приравняв производную нулю и решив полученное квадратное уравнение, найдем две критические точки: 
и 
. Ось разбивается этими точками на три интервала: 
, 
и 
, причем на каждом из них 
сохраняет знак. Определим эти знаки, например, вычислив в произвольных точках указанных интервалов, получим:
на и , и 
на .
Отсюда в силу теорем 1-3 заключаем, что функция возрастает на интервалах и , убывает на интервале , в точке 
достигает максимального значения 
, а в точке 
- минимального значения 
.
б) Пусть 
. Тогда 
, и единственной критической точкой является 
. Так как знак производной не меняется при переходе через эту точку, то она не является точкой экстремума. График этой функции приведен в § 1 на рис. 7.
в) Пусть 
, 
. Тогда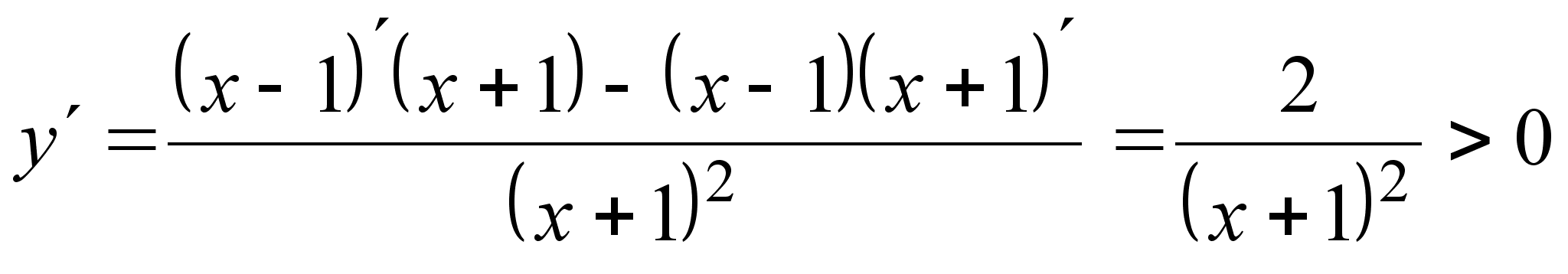 
при всех . Это означает, что данная функция возрастает на интервалах (
) и (
).
г) Точка является критической точкой функции 
- производная функции в этой точке не существует. Функция достигает в этой точке минимума, что иллюстрирует ее график (рис. 5).
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
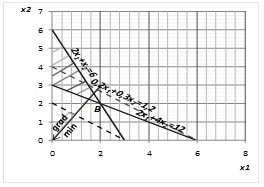
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...
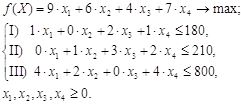
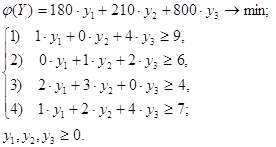
0 комментариев