Навигация
Определение производной и правила дифференцирования
1. Определение производной и правила дифференцирования
Пусть функция
![]() определена
в некоторой
окрестности
точки
определена
в некоторой
окрестности
точки ![]() .
Пусть
.
Пусть ![]() – приращение
аргумента
в точке
– приращение
аргумента
в точке ![]() ,
а
,
а ![]() – соответствующее
приращение
функции. Составим
отношение
– соответствующее
приращение
функции. Составим
отношение ![]() этих приращений
и рассмотрим
его предел при
этих приращений
и рассмотрим
его предел при
![]() .
Если указанный
предел существует,
то он называется
производной
функции
.
Если указанный
предел существует,
то он называется
производной
функции ![]() в точке
в точке ![]() и обозначается
и обозначается
![]() ,
,
![]() или
или ![]() ,
то есть
,
то есть
![]() .
.
Операция вычисления
производной
называется
дифференцированием,
а функция, имеющая
производную
в точке, – дифференцируемой
в этой точке.
Если функция
имеет производную
в каждой точке
интервала ![]() ,
то она называется
дифференцируемой
на этом интервале.
,
то она называется
дифференцируемой
на этом интервале.
Примеры. Найдем производные
функций в
произвольной
точке ![]() :
:
а) ![]() ,
,
![]() ;
;
б)
![]() ,
,
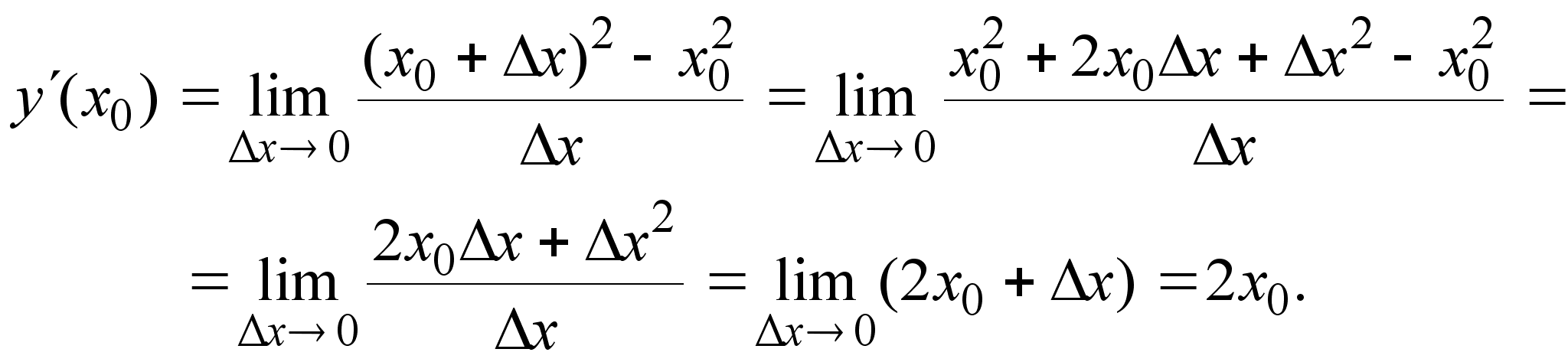
Заметим, что на практике при вычислении производных редко прибегают к определению. Вместо этого используют таблицу, содержащую выражения для производных всех основных элементарных функций, а также правила дифференцирования, позволяющие находить производную суммы, разности, произведения, частного и композиции функций.
Приведем таблицу производных некоторых основных элементарных функций и правила дифференцирования.
Таблица производных1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ,
,
где ![]() ,
, ![]() и
и ![]() - произвольные постоянные,
- произвольные постоянные, ![]() ,
, ![]() .
.
Примеры. Получим некоторые следствия формулы 2:
а) ![]() ,
,
б) ![]() ;
;
в) 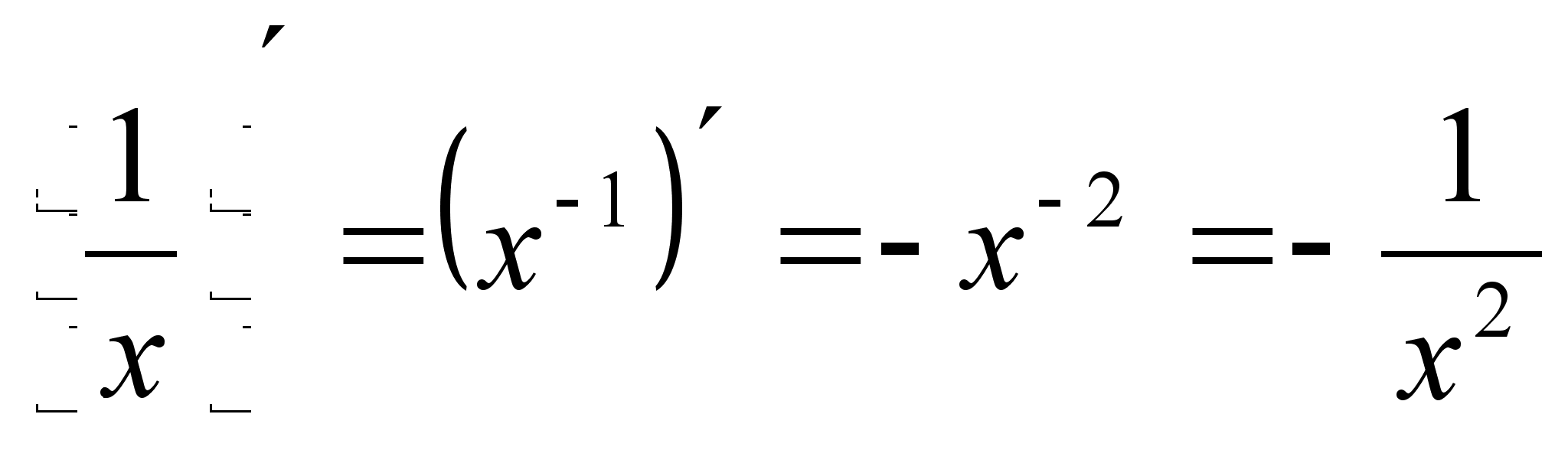 .
.
Правила дифференцирования
![]() ;
;
![]() , где
, где ![]() - постоянная;
- постоянная;
![]() ;
;
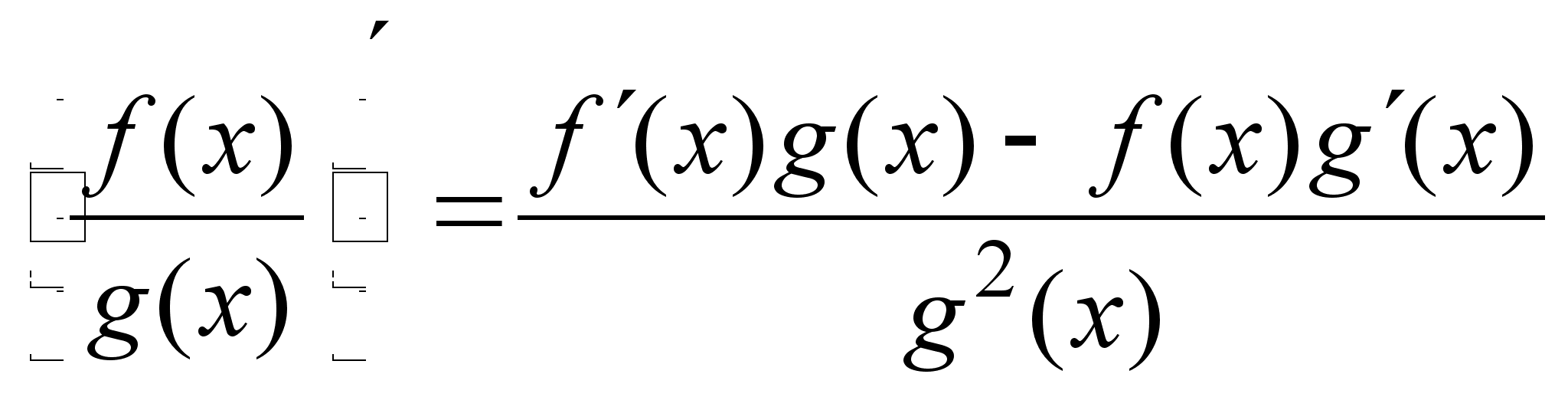 ;
;
если ![]() , а
, а ![]() , то производная сложной функции
, то производная сложной функции ![]() находится по формуле
находится по формуле
![]() ,
,
где индексы указывают, по какому аргументу производится дифференцирование.
Примеры. Найдем производные функций, используя правила 1-4:
а) ![]() ;
;
б) ![]() ;
;
в) 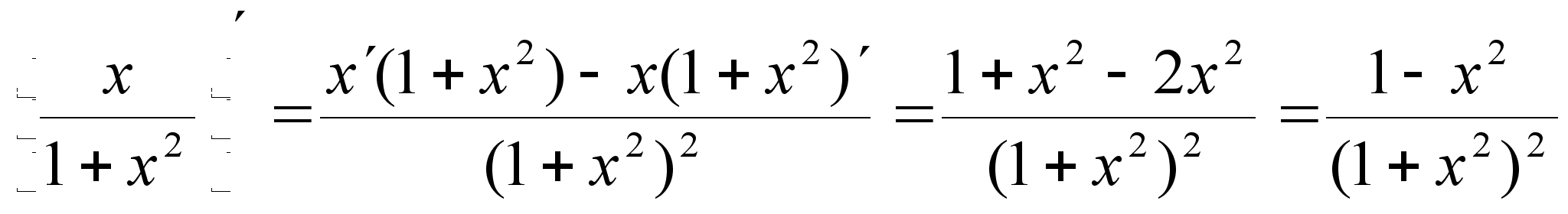 ;
;
Примеры. Найдем производные сложных функций по правилу 5:
а) ![]() ; положим
; положим ![]() , тогда
, тогда ![]() , и, следовательно,
, и, следовательно,
![]() ;
;
б) ![]() ; положим
; положим ![]() , тогда
, тогда ![]() , и
, и
![]() .
.
Заметим, что производная ![]() , называемая также первой производной функции
, называемая также первой производной функции ![]() , сама является функцией аргумента
, сама является функцией аргумента ![]() . Производная этой функции называется второй производной функции
. Производная этой функции называется второй производной функции ![]() и обозначается
и обозначается ![]() , то есть
, то есть ![]() . Аналогично можно ввести третью и более высокие производные.
. Аналогично можно ввести третью и более высокие производные.
Примеры. Найдем вторые производные:
а) ![]() ;
;
б) ![]() .
.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
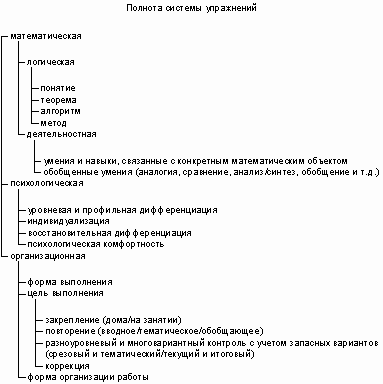
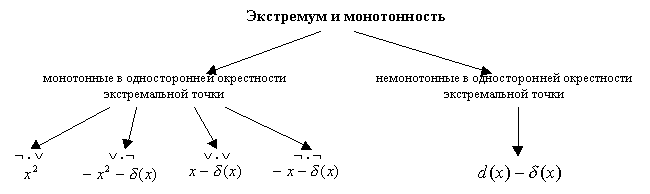
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
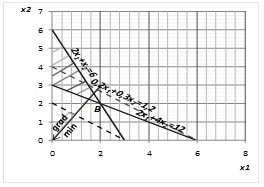
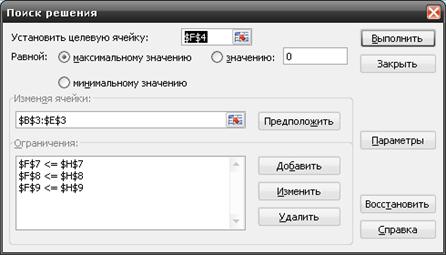
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





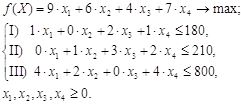
0 комментариев