Навигация
Математические модели некоторых процессов
3. Математические модели некоторых процессов
Рассмотрим примеры задач, исследование которых проводится с использованием обыкновенных дифференциальных уравнений.
Пример (закон
роста населения
Земли). Пусть
![]() - число людей
на Земле в момент
времени
- число людей
на Земле в момент
времени ![]() .
Демографические
данные показывают,
что за небольшой
интервал времени
.
Демографические
данные показывают,
что за небольшой
интервал времени
![]() прирост населения
прирост населения
![]() пропорционален
квадрату числа
людей и интервалу
времени:
пропорционален
квадрату числа
людей и интервалу
времени:
![]() ,
,
где ![]() - некоторая
постоянная.
Разделив левую
и правую части
этого равенства
на
- некоторая
постоянная.
Разделив левую
и правую части
этого равенства
на ![]() и перейдя к
пределу при
и перейдя к
пределу при
![]() ,
получим уравнение
,
получим уравнение
![]() , (5)
, (5)
где ![]() - дифференцируемая
функция, приближающая
функцию
- дифференцируемая
функция, приближающая
функцию ![]() .
Уравнение (5)
аналогично
уравнению (4),
рассмотренному
выше. Его общее
решение имеет
вид
.
Уравнение (5)
аналогично
уравнению (4),
рассмотренному
выше. Его общее
решение имеет
вид ![]() .
Заметим, что
известные
демографические
данные хорошо
согласуются
с частным решением
.
Заметим, что
известные
демографические
данные хорошо
согласуются
с частным решением
![]() ,
,
где время ![]() исчисляется
в годах от начала
нашей эры. Функция
исчисляется
в годах от начала
нашей эры. Функция
![]() не определена
при
не определена
при ![]() ,
поэтому закон
роста населения
в будущем должен
измениться.
,
поэтому закон
роста населения
в будущем должен
измениться.
Пример (модель
производства).
Пусть ![]() - интенсивность
выпуска продукции
некоторым
предприятием
в момент времени
- интенсивность
выпуска продукции
некоторым
предприятием
в момент времени
![]() ,
а
,
а ![]() - цена продукции.
Доход от продажи
этой продукции
составляет
- цена продукции.
Доход от продажи
этой продукции
составляет
![]() .
Пусть часть
вырученных
средств, равная
.
Пусть часть
вырученных
средств, равная
![]() , (6)
, (6)
где ![]() - некоторое
число, направляется
на расширение
производства.
Предположим,
что скорость
изменения
интенсивности
выпуска продукции
прямо пропорциональна
объему инвестиций:
- некоторое
число, направляется
на расширение
производства.
Предположим,
что скорость
изменения
интенсивности
выпуска продукции
прямо пропорциональна
объему инвестиций:
![]() , (7)
, (7)
где
![]() -
постоянная.
Из (6) и (7) получаем
уравнение
-
постоянная.
Из (6) и (7) получаем
уравнение
![]() , (8)
, (8)
общее решение
которого при
постоянном
![]() имеет вид
имеет вид ![]() ,
где
,
где ![]() .
Если задано
начальное
условие
.
Если задано
начальное
условие
![]() , (9)
, (9)
то решением задачи Коши (8), (9) является функция
![]() .
.
Уравнение (8) называется уравнением естественного роста. Им описываются также процессы радиоактивного распада в физике и размножения бактерий в биологии.
На практике
с увеличением
выпуска продукции
происходит
насыщение рынка
и цена падает.
Если, например,
![]() ,
где
,
где ![]() и
и ![]() -
положительные
постоянные,
то вместо (8) получим
уравнение
-
положительные
постоянные,
то вместо (8) получим
уравнение
![]() , (10)
, (10)
аналогичное уравнению, рассматриваемому в следующем примере.
Пример (модель
рекламы). Пусть
![]() - число людей,
знающих к моменту
времени
- число людей,
знающих к моменту
времени ![]() некоторую
новость, а
некоторую
новость, а ![]() -
общее число
людей. Будем
предполагать,
что скорость
распространения
новости
-
общее число
людей. Будем
предполагать,
что скорость
распространения
новости ![]() прямо пропорциональна
как числу людей
прямо пропорциональна
как числу людей
![]() ,
уже ее знающих,
так и числу
людей
,
уже ее знающих,
так и числу
людей ![]() ,
еще не знающих
новости, то
есть
,
еще не знающих
новости, то
есть
![]() , (11)
, (11)
где ![]() -
постоянная.
Разделив переменные
в этом уравнении,
получим
-
постоянная.
Разделив переменные
в этом уравнении,
получим
![]() ,
,
откуда, используя результат последнего примера § 4, найдем
![]()
или
![]() .
.
График этой
функции называется
логистической
кривой. Для
случая ![]() ,
соответстщего
условию, что
в момент
,
соответстщего
условию, что
в момент ![]() половина людей
знает новость
(
половина людей
знает новость
(![]() ),
эта
),
эта
кривая представлена на рис. 15.
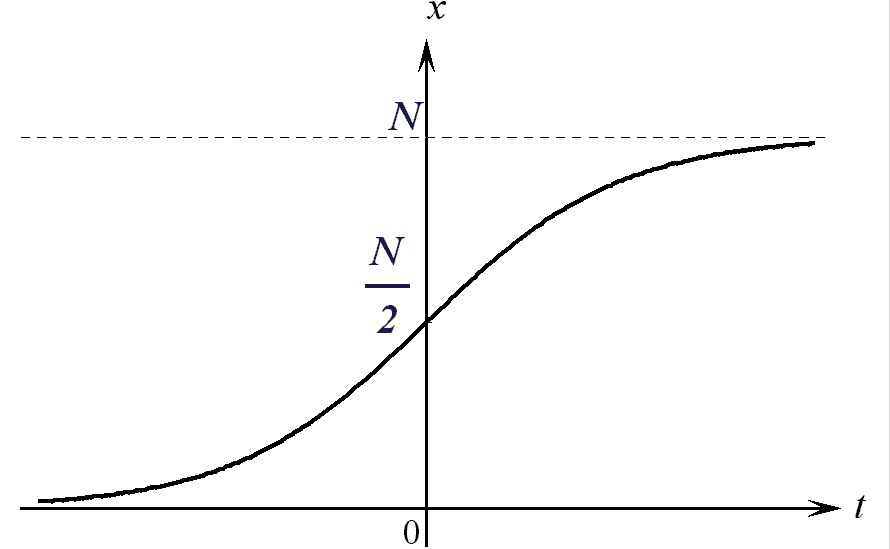
Рис.15.
Рассматриваемое
уравнение
обладает также
решениями ![]() и
и ![]() ,
обращающими
в ноль его правую
часть. Эти решения
соответствуют
ситуациям,
когда новость
не распространяется:
в первом случае
в начальный
момент ее никто
не знает, а во
втором - знают
все.
,
обращающими
в ноль его правую
часть. Эти решения
соответствуют
ситуациям,
когда новость
не распространяется:
в первом случае
в начальный
момент ее никто
не знает, а во
втором - знают
все.
Отметим, что уравнения (10) и (11), описывающие совершенно разные процессы, по существу, совпадают. Уравнения того же типа возникают при описании динамики эпидемий, процессов размножения бактерий в ограниченной среде обитания, применяются в математической теории экологии.
Упражнения
1. Решить уравнения:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4)![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() ;
;
21) ![]() ;
;
22) ![]() ;
;
23) ![]() ;
;
24) ![]() ;
;
25) ![]() ;
;
26) ![]() .
.
2. Решить задачи Коши:
1) ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ;
;
4) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() ;
;
6) ![]() ,
, ![]() ;
;
7) ![]() ,
, ![]() ;
;
8) ![]() ,
, ![]() ;
;
9) ![]() ,
, ![]() ;
;
10) ![]() ,
, ![]() ;
;
11) ![]() ,
, ![]() ;
;
12) ![]() ,
, ![]() ;
;
13) ![]() ,
, ![]() ;
;
14) ![]() ,
, ![]() ;
;
15) ![]() ,
, ![]() ,
,
16) ![]() ,
, ![]() ;
;
17) ![]() ,
, ![]() ;
;
18) ![]() ,
, ![]() ;
;
19) ![]() ,
, ![]() ;
;
20) ![]() ,
, ![]() .
.
Ответы
1.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) ![]() ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) Общее решение находится
из уравнения ![]() ;
;
21) ![]() ;
;
22) ![]() ;
;
23) ![]() ;
;
24 ) ![]() ;
;
25) ![]() ;
;
26) ![]() .
.
2.
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ;
;
5) ![]() ;
;
6) 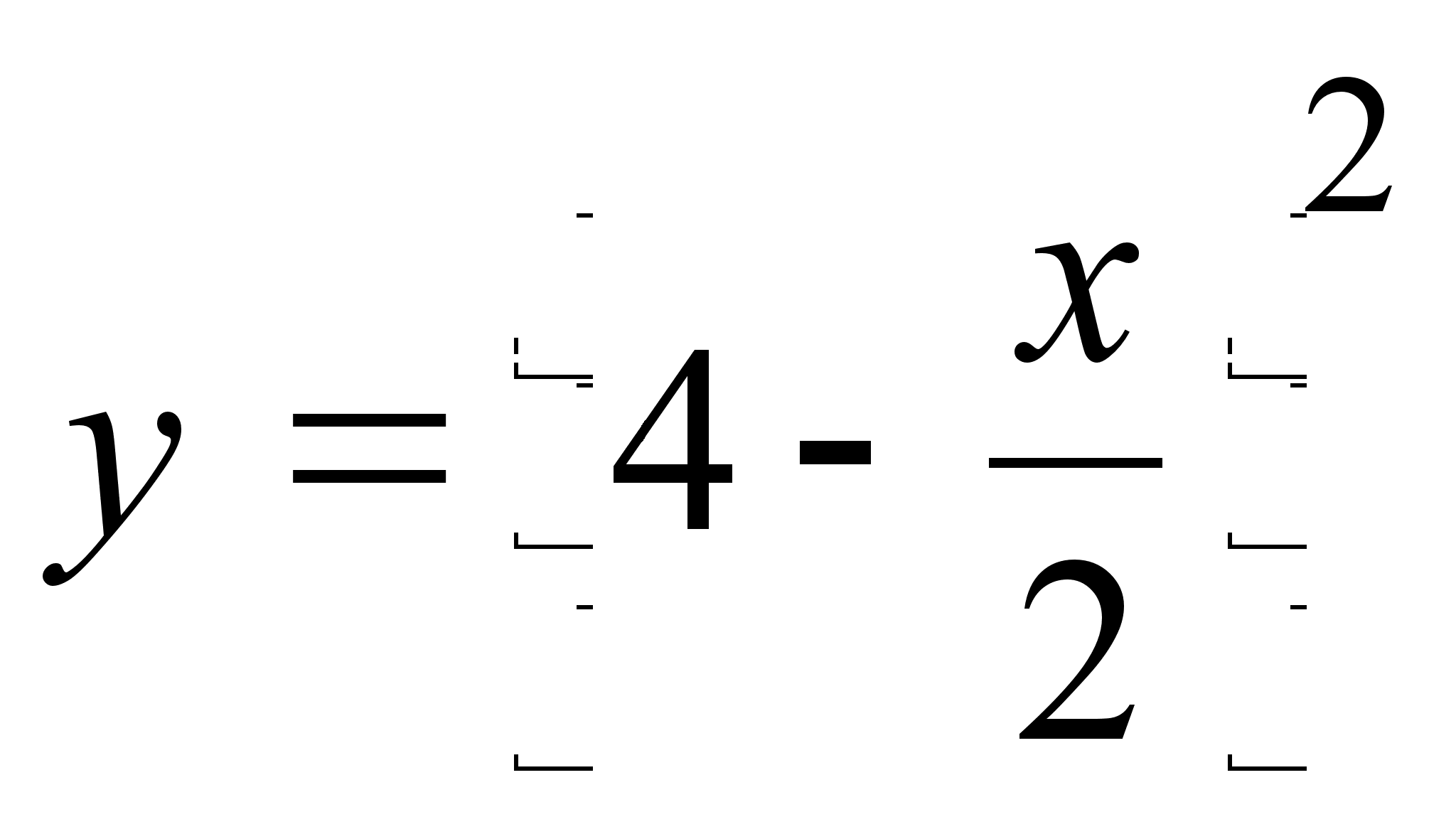 ;
;
7) ![]() ;
;
8) ![]() ;
;
9) ![]() ;
;
10) ![]() ;
;
11) ![]() ;
;
12) ![]() ;
;
13) ![]() ;
;
14) ![]() ;
;
15) ![]() и
и ![]() ;
;
16) ![]() ;
;
17) ![]() ;
;
18) ![]() ;
;
19) ![]() ;
;
20) ![]() .
.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
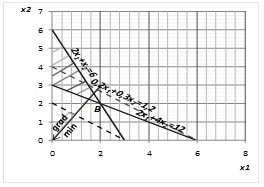
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





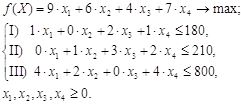
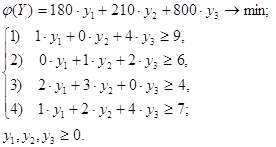
0 комментариев