Навигация
Формула Ньютона – Лейбница
3. Формула Ньютона – Лейбница
Если функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() и
и ![]() - любая ее первообразная
на этом отрезке,
то справедлива
основная формула
интегрального
исчисления:
- любая ее первообразная
на этом отрезке,
то справедлива
основная формула
интегрального
исчисления:
![]() ,
,
называемая
формулой
Ньютона-Лейбница.
Используя
краткое обозначение ![]() ,
эту формулу
можно записать
в виде
,
эту формулу
можно записать
в виде
![]() .
.
Таким образом, вычисление определенного интеграла от непрерывной функции сводится к отысканию ее первообразной, то есть, по существу, неопределенного интеграла, что позволяет использовать методы, изложенные в § 4.
Пример.
Найдем интеграл ![]() .
Поскольку
.
Поскольку ![]() ,
то по формуле
Ньютона-Лейбница
получаем
,
то по формуле
Ньютона-Лейбница
получаем
 .
.
Пример.
Площадь ![]() криволинейной
трапеции,
ограниченной
графиком функции
криволинейной
трапеции,
ограниченной
графиком функции ![]() ,
осью
,
осью ![]() и прямыми
и прямыми ![]() и
и ![]() ,
равна
,
равна
![]() .
.
Упражнения
1. Вычислить определенные интегралы:
1) ![]() ; 6)
; 6) 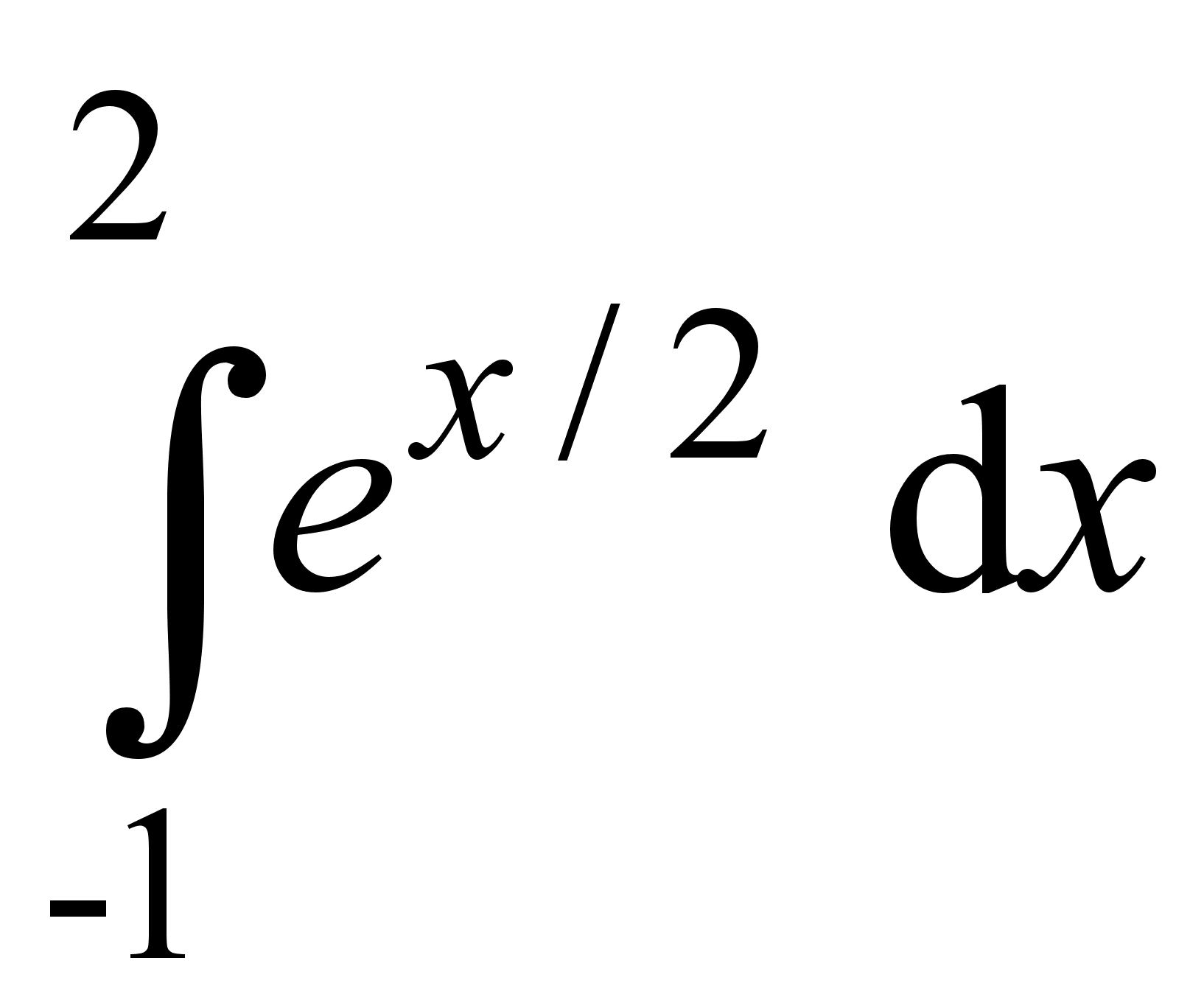 ; 11)
; 11) 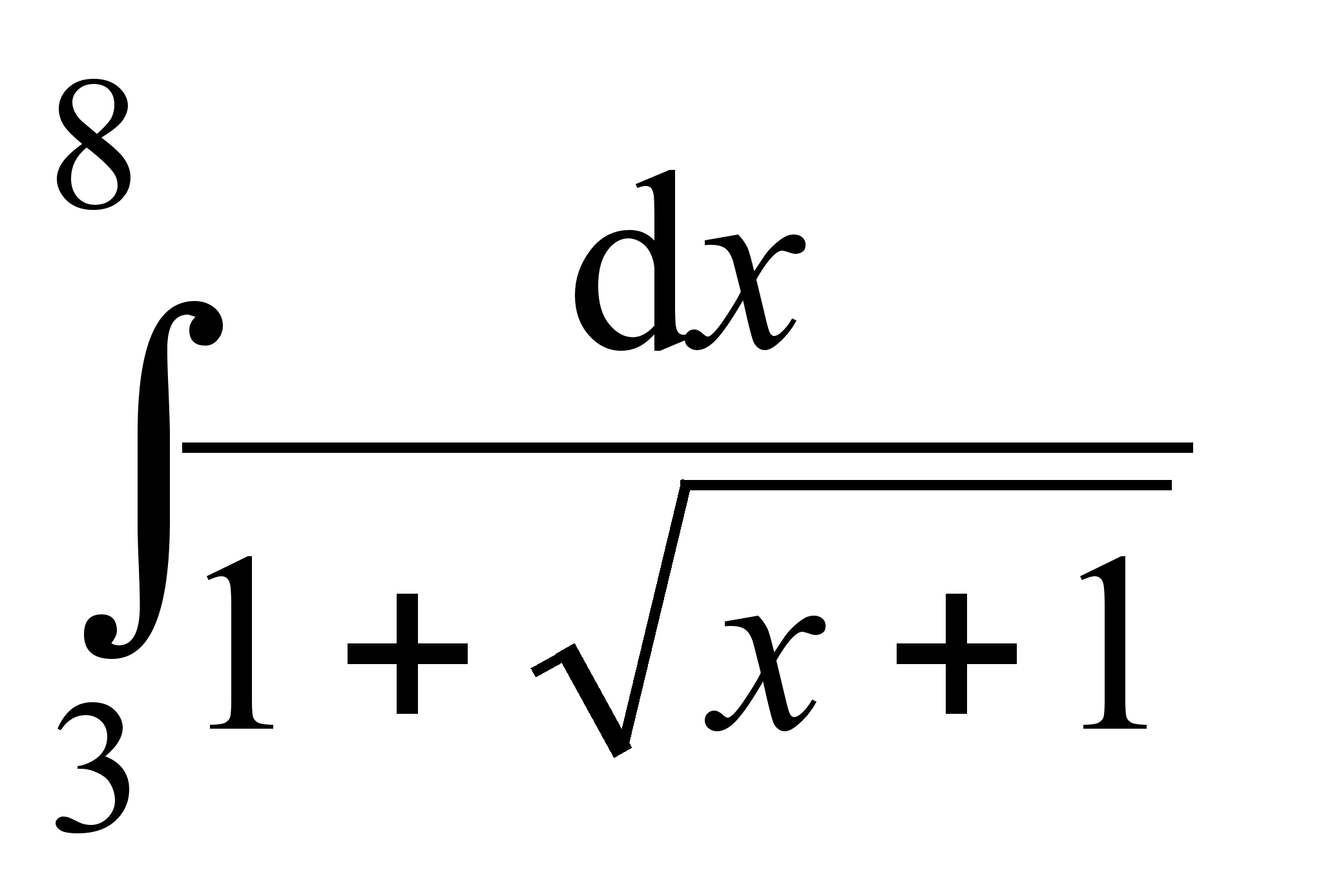 ;
;
2) 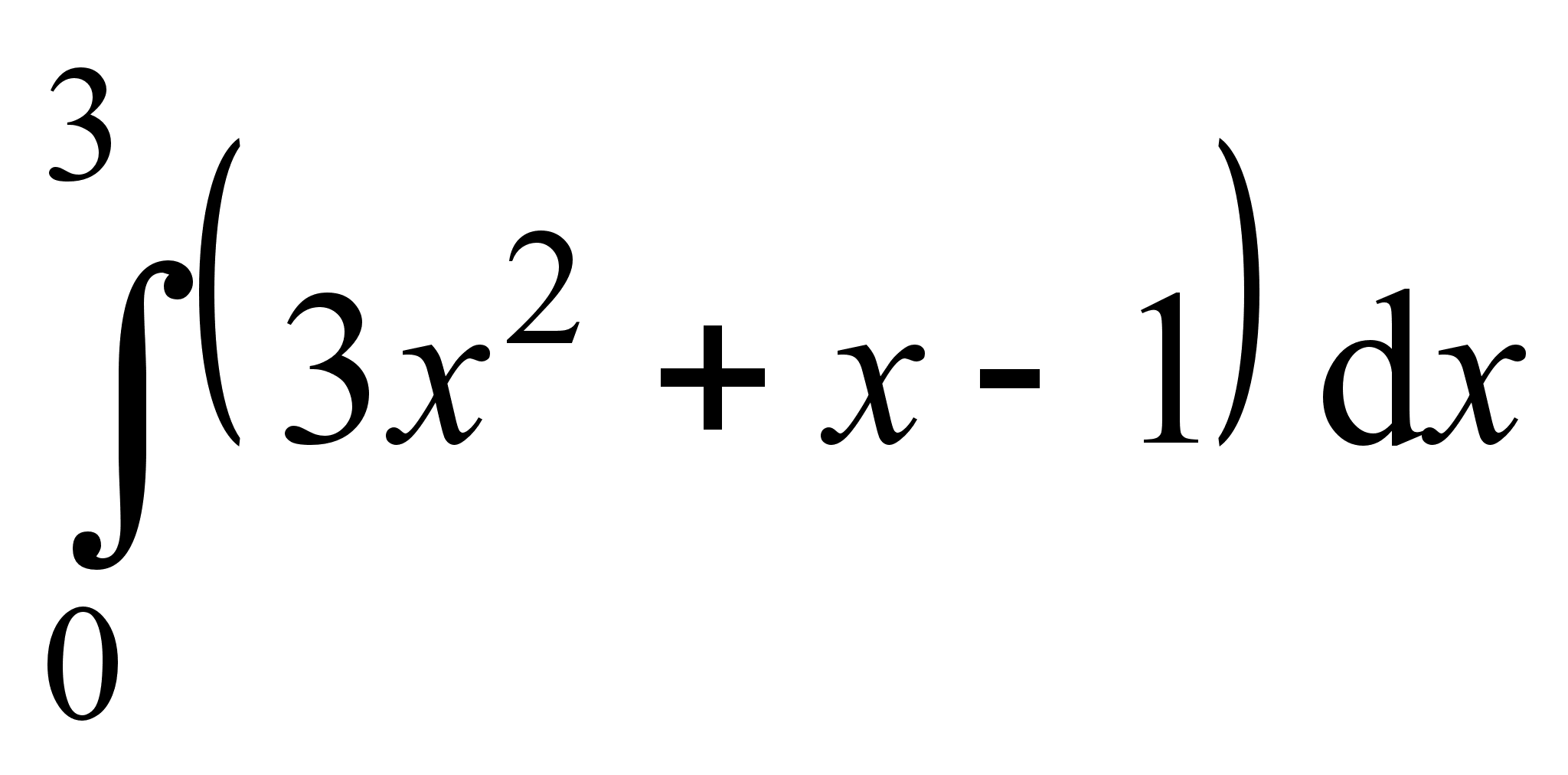 ; 7)
; 7) 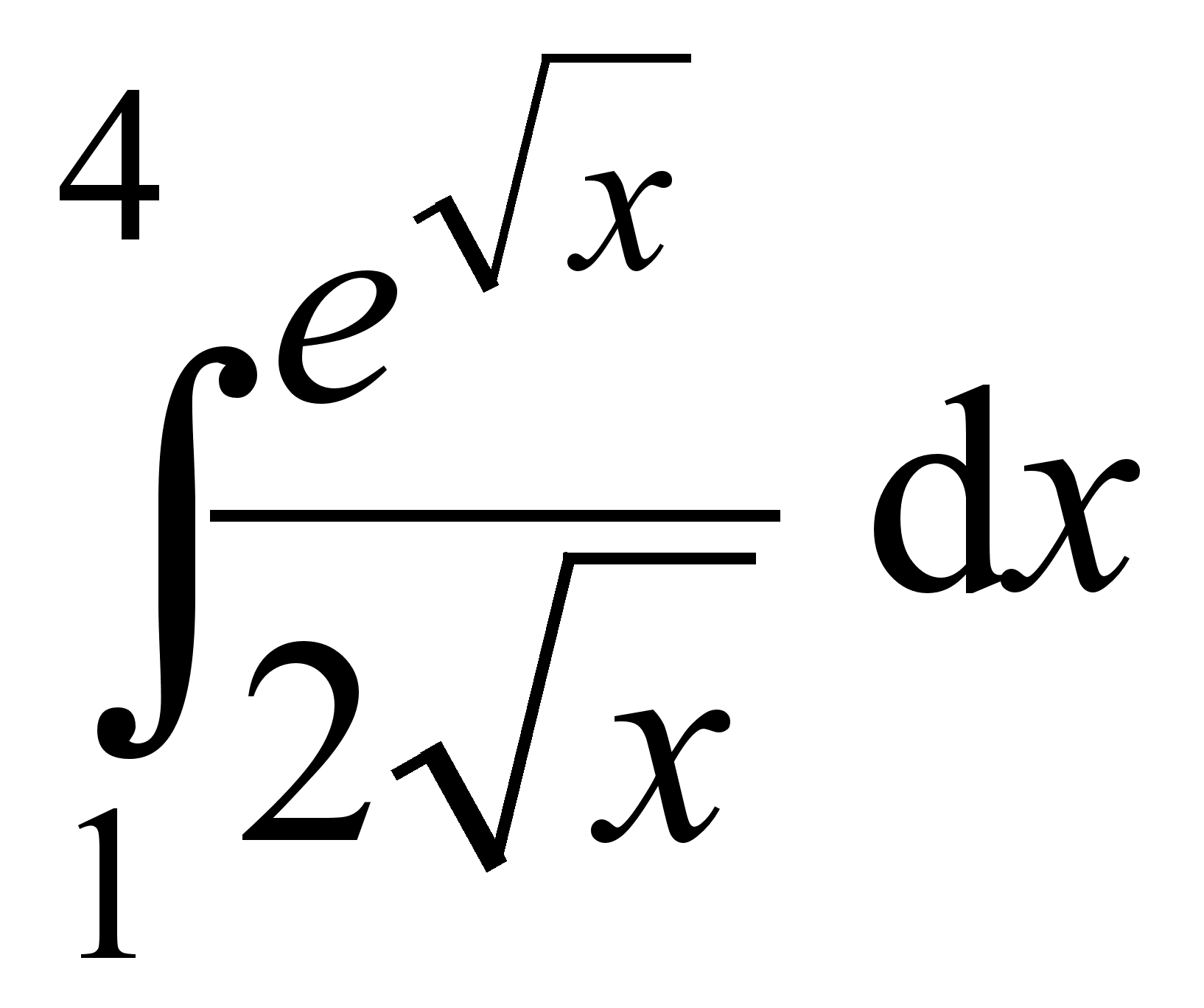 ; 12)
; 12) 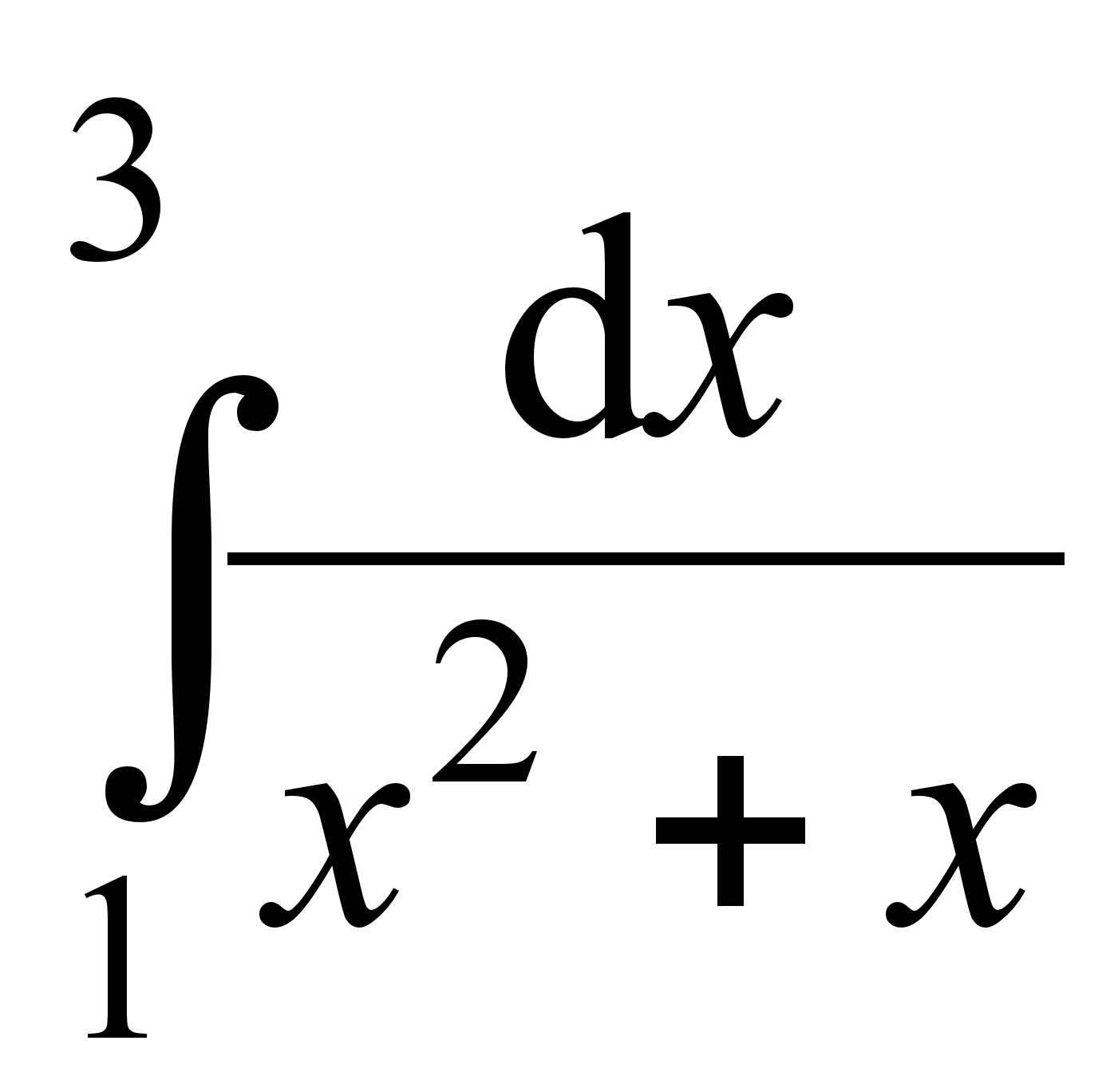 ;
;
3) ![]() ; 8)
; 8)  ; 13)
; 13) 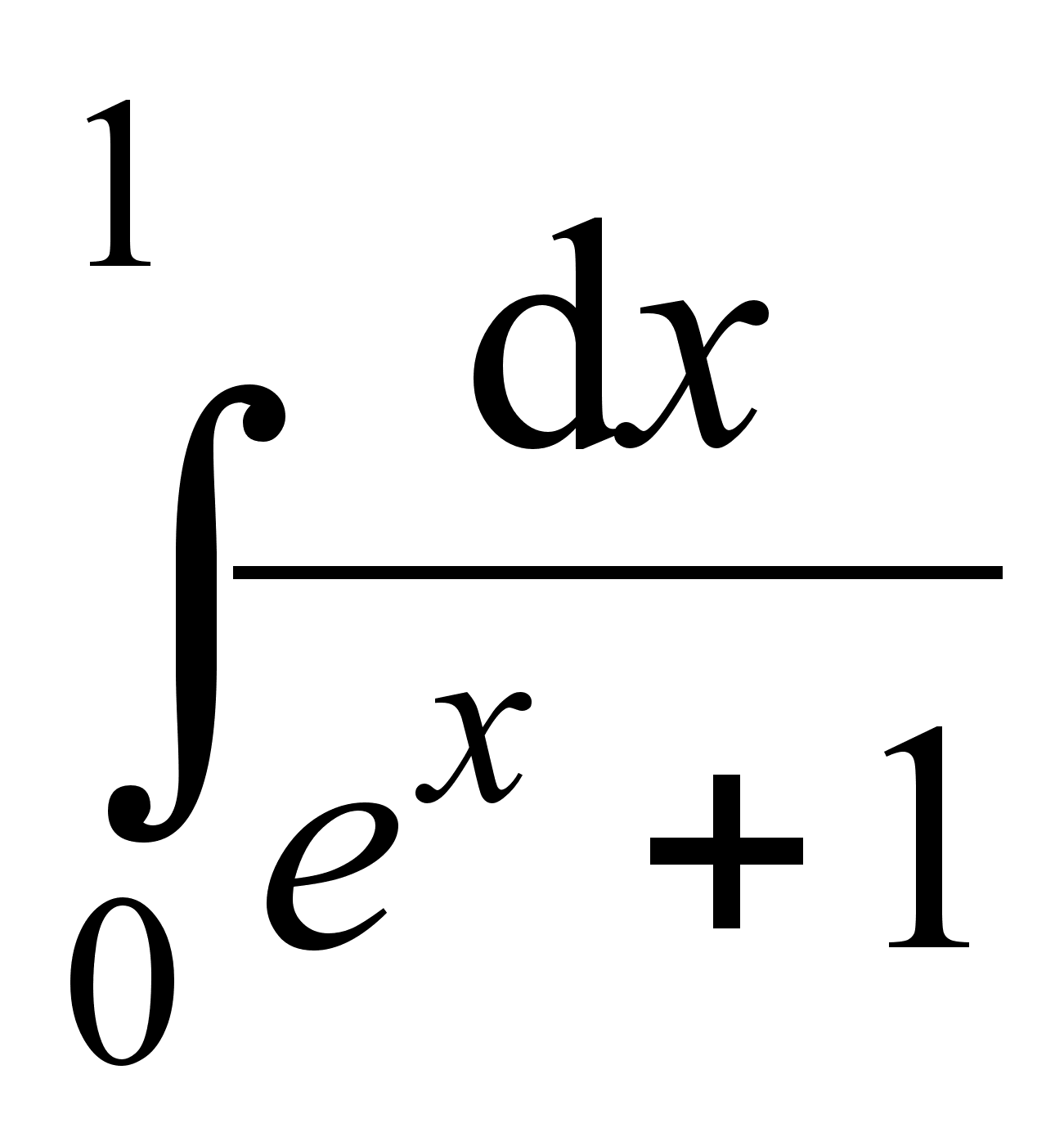 ;
;
4) ![]() ; 9)
; 9) 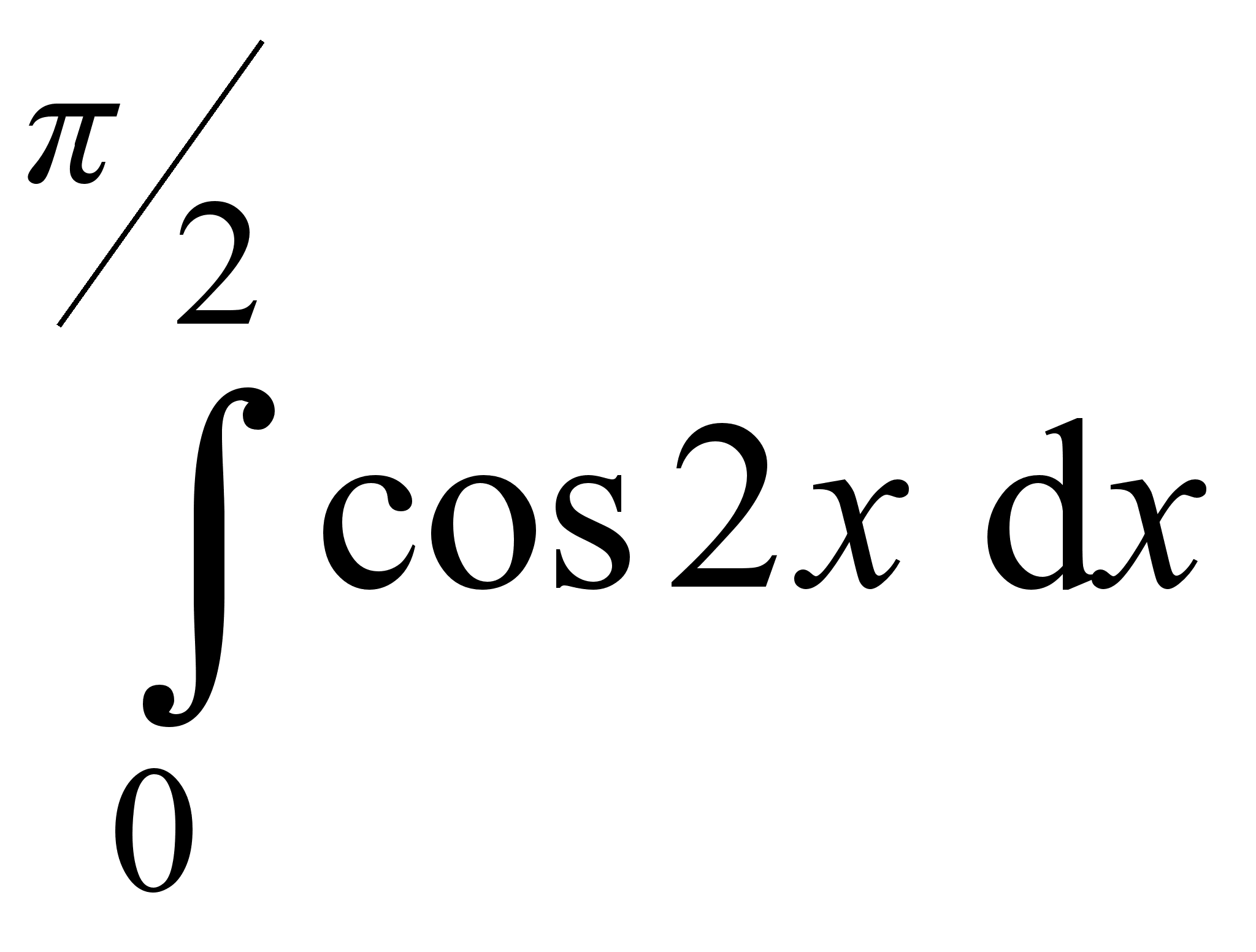 ; 14)
; 14) 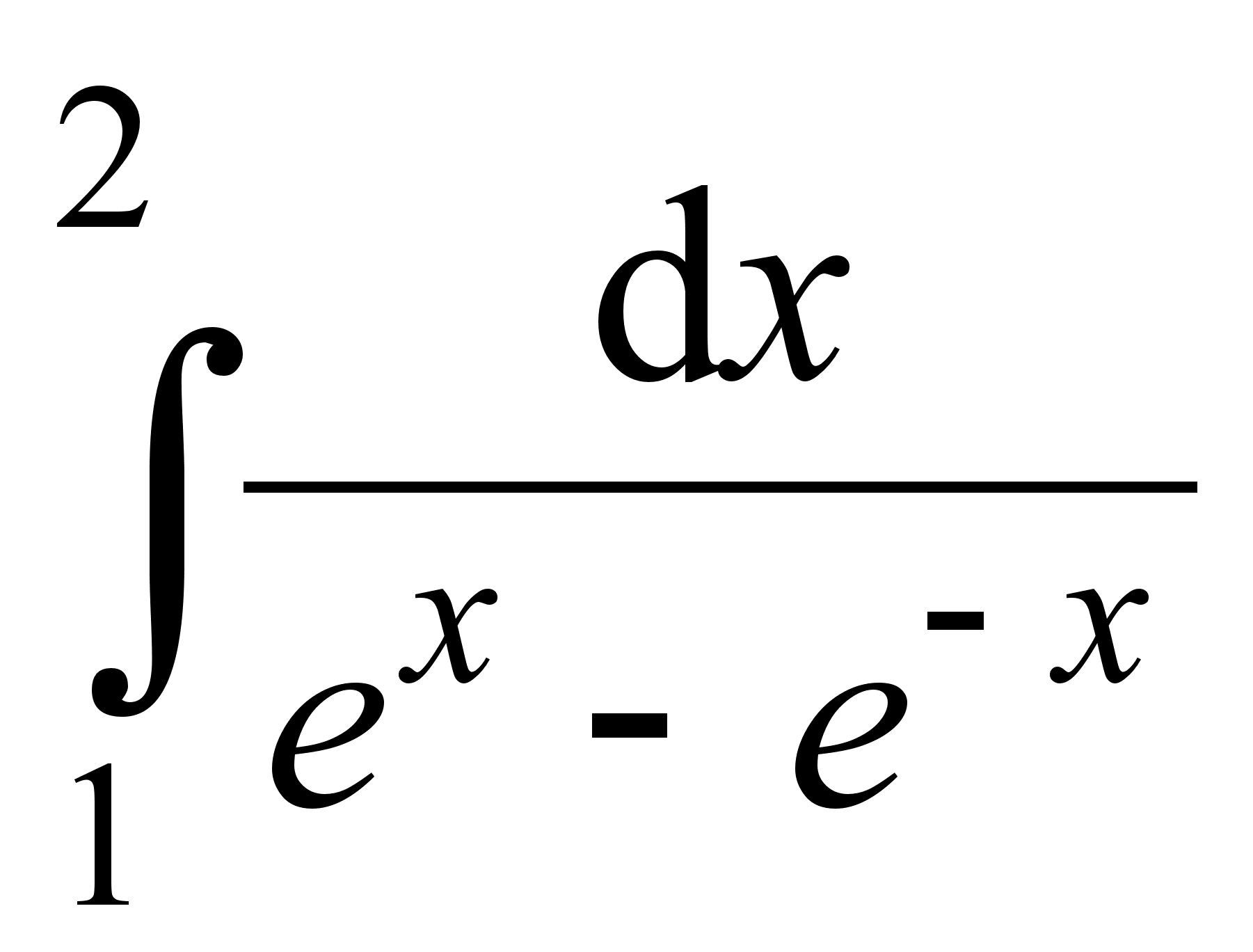 .
.
5) 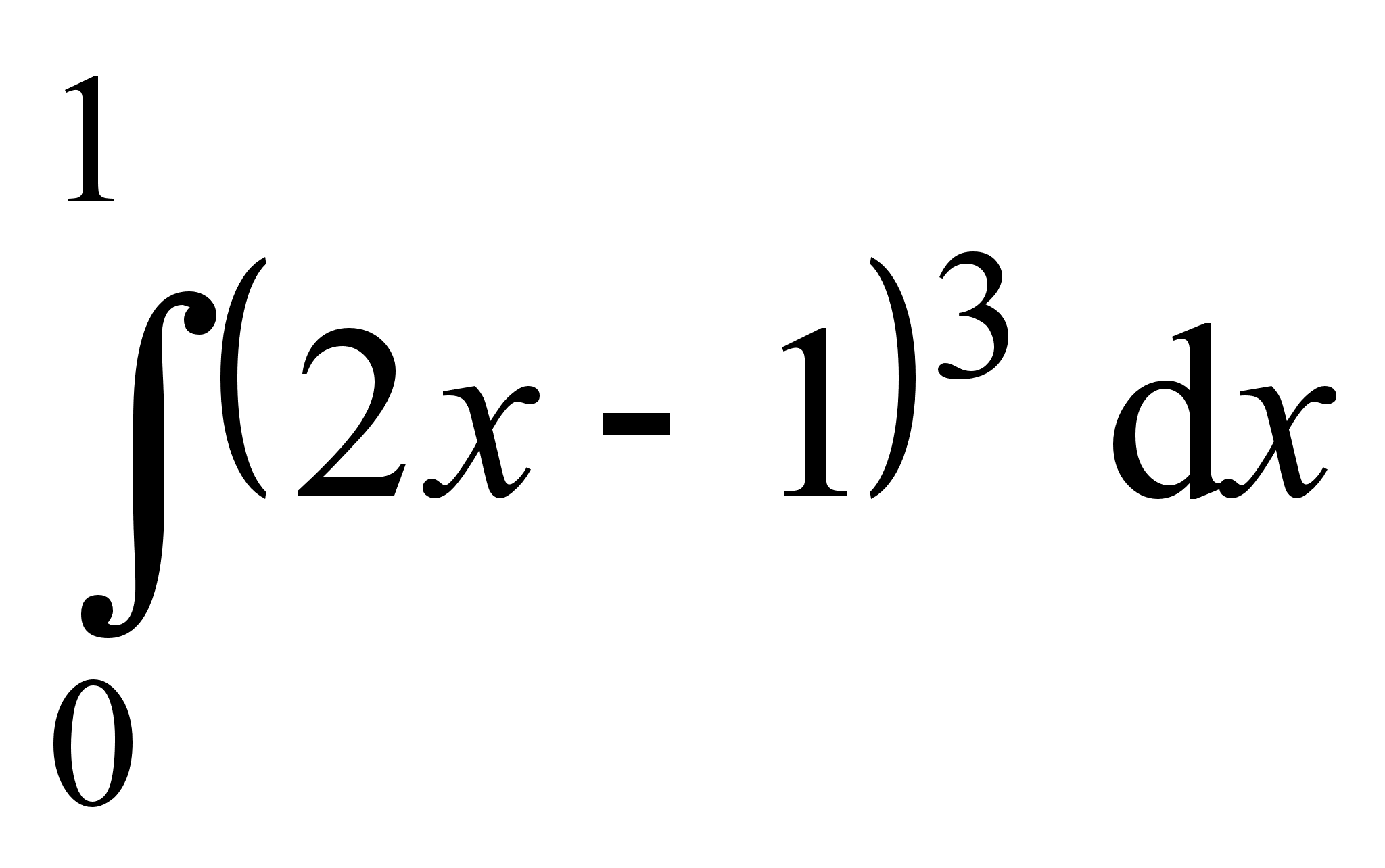 ; 10)
; 10) 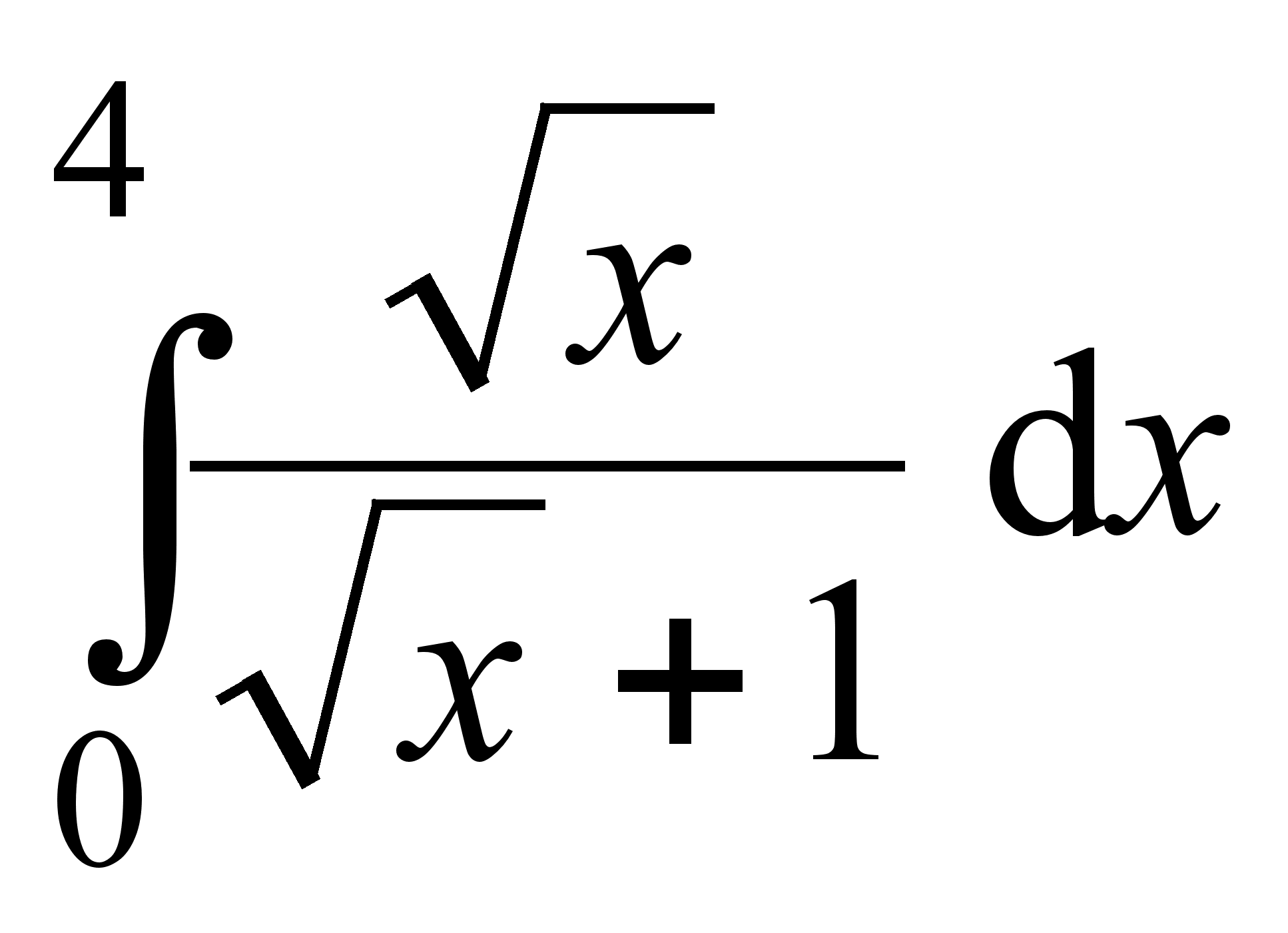 ;
;
2. Найти площади фигур, ограниченных линиями:
1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() .
.
Ответы
1. 1) 4; 2) ![]() ; 3)
; 3) ![]() ; 4) 1; 5) 0; 6) 2(
; 4) 1; 5) 0; 6) 2(![]() ); 7)
); 7) ![]() ; 8) 2; 9) 0; 10)
; 8) 2; 9) 0; 10) ![]() ;
;
11) ![]() ; 12)
; 12) ![]() : 13)
: 13) ![]() ; 14)
; 14) 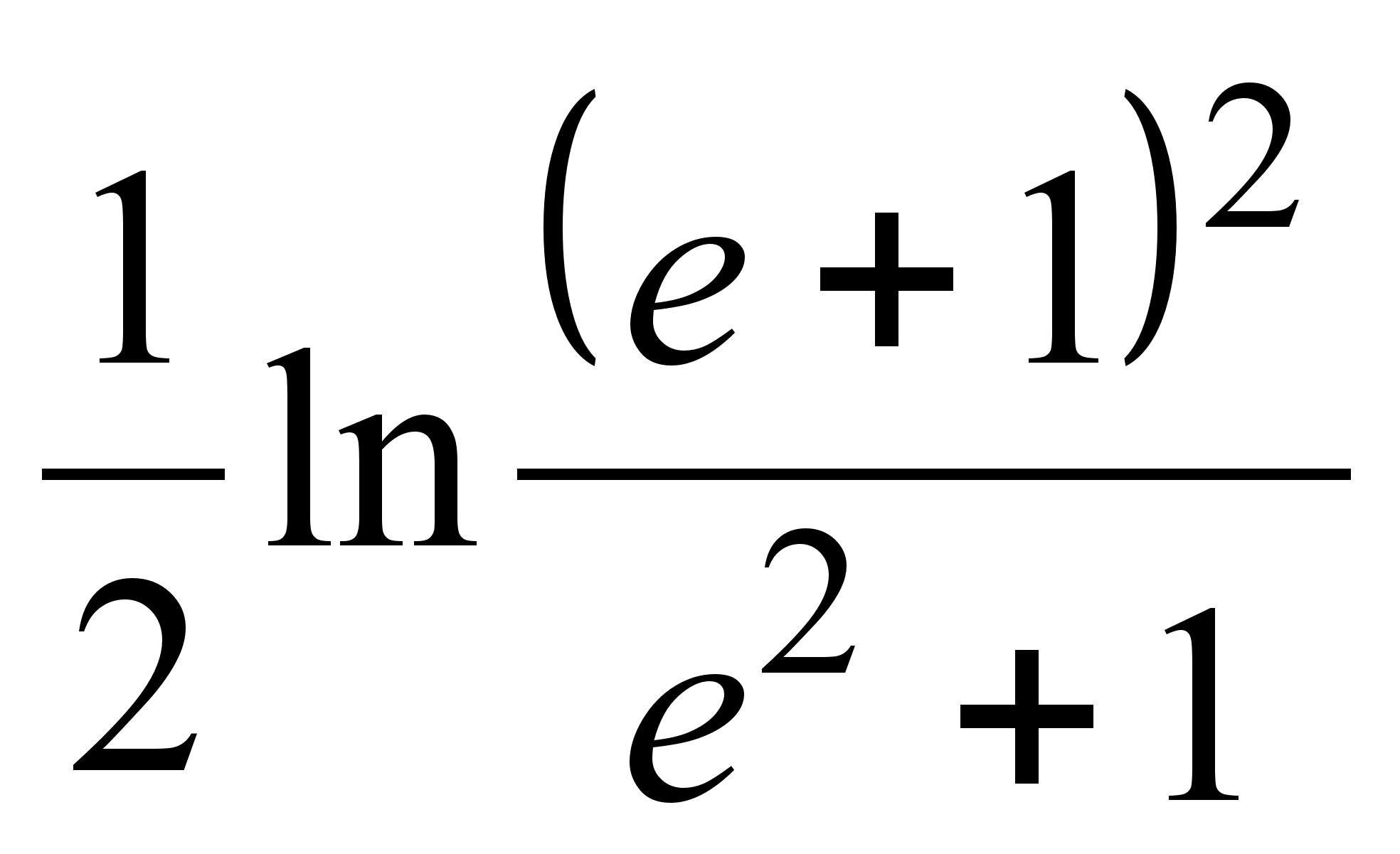 ;
;
2. 1) 12; 2) 1; 3) ![]() ;
Графики функций
;
Графики функций ![]() и
и ![]() пересекаются
в точках с абсциссами
пересекаются
в точках с абсциссами ![]() .
Площадь фигуры
может быть
вычислена как
разность двух
площадей:
.
Площадь фигуры
может быть
вычислена как
разность двух
площадей: 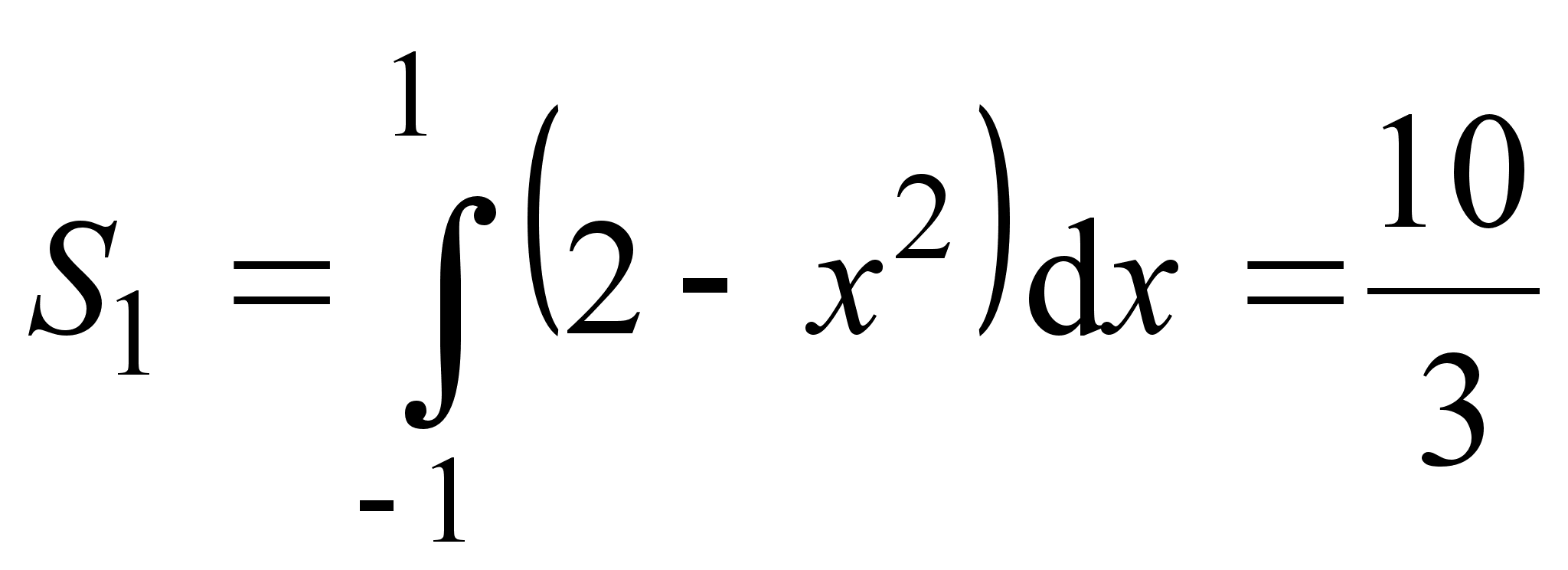 и
и 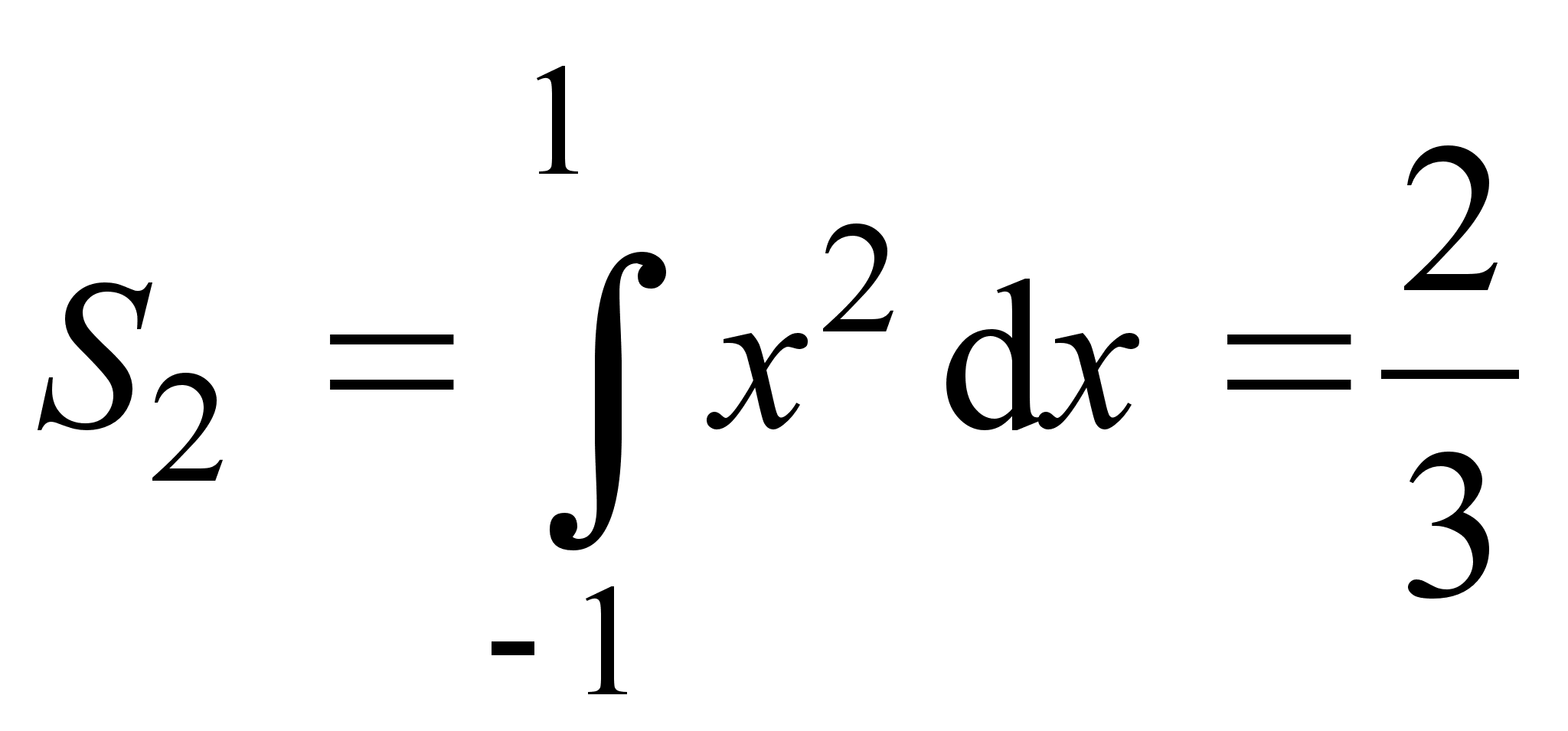 .
.
§ 6. Функции нескольких переменных
Функции нескольких переменных возникают при необходимости учета зависимости некоторой величины более чем от одного фактора. Многие понятия: предел, непрерывность, производная и другие, введенные для функций одной переменной, переносятся на случай функций нескольких переменных.
Мы ограничимся здесь рассмотрением функций двух переменных. Для функций большего числа переменных указанные понятия вводятся аналогично.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
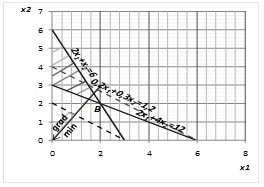
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





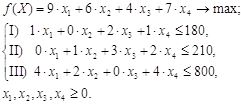
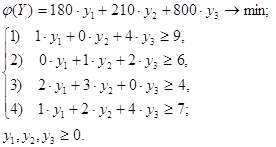
0 комментариев