Навигация
1. Определение
Пусть функция ![]() определена
на отрезке
определена
на отрезке ![]() .
Разобьем отрезок
на
.
Разобьем отрезок
на ![]() частей точками
частей точками ![]() (
(![]() )
такими, что
)
такими, что ![]() .
Длины полученных
отрезков обозначим
.
Длины полученных
отрезков обозначим ![]() (
(![]() ),
и пусть
),
и пусть ![]() – наибольшая
из этих длин.
Выберем на
каждом из отрезков
разбиения
произвольную
точку
– наибольшая
из этих длин.
Выберем на
каждом из отрезков
разбиения
произвольную
точку ![]() и составим
сумму
и составим
сумму
![]() , (1)
, (1)
которую
назовем интегральной
суммой для
функции ![]() .
.
Рассмотрим
интегральные
суммы, соответствующие разбиениям
отрезка ![]() при различных
значениях
при различных
значениях ![]() .
Если существует
предел таких
сумм при
.
Если существует
предел таких
сумм при ![]() ,
то он называется
определенным
интегралом
функции
,
то он называется
определенным
интегралом
функции ![]() на отрезке
на отрезке ![]() и обозначается
и обозначается
![]() ,
,
при
этом функция ![]() называется
интегрируемой
(по Риману) на
отрезке
называется
интегрируемой
(по Риману) на
отрезке ![]() ,
числа
,
числа ![]() и
и ![]() называются
соответственно
нижним и верхним
пределами
интегрирования.
называются
соответственно
нижним и верхним
пределами
интегрирования.
Заметим, что всякая непрерывная на отрезке функция интегрируема на этом отрезке.
Пример. Функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() и, следовательно,
интегрируема
на нем. Чтобы
вычислить
интеграл
и, следовательно,
интегрируема
на нем. Чтобы
вычислить
интеграл ![]() ,
достаточно
рассмотреть
любую последовательность
разбиений
отрезка
,
достаточно
рассмотреть
любую последовательность
разбиений
отрезка ![]() ,
для которой
,
для которой ![]() ,
и найти предел
соответствующей
последовательности
интегральных
сумм. При этом
промежуточные
точки
,
и найти предел
соответствующей
последовательности
интегральных
сумм. При этом
промежуточные
точки ![]() для каждого
разбиения можно
выбирать произвольно.
Рассмотрим
равномерные
разбиения вида
для каждого
разбиения можно
выбирать произвольно.
Рассмотрим
равномерные
разбиения вида ![]() ,
, ![]() ,
а в качестве
,
а в качестве ![]() выберем правые
концы отрезков
выберем правые
концы отрезков ![]() ,
то есть положим
,
то есть положим ![]() ,
, ![]() .
В этом случае
имеем
.
В этом случае
имеем ![]() ,
, ![]() ,
и интегральная
сумма (1) принимает
вид
,
и интегральная
сумма (1) принимает
вид
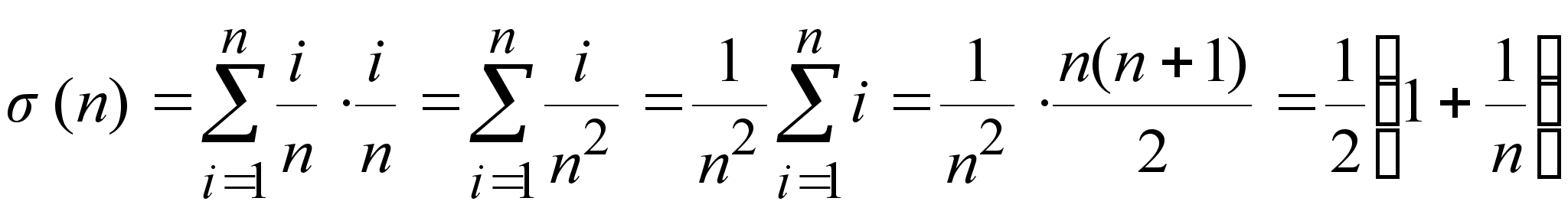 .
.
Переходя
к пределу при ![]() ,
получаем
,
получаем
![]() .
.
2. Геометрический смысл
Пусть функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() и неотрицательна:
и неотрицательна: ![]() .
Фигуру, ограниченную
графиком функции
.
Фигуру, ограниченную
графиком функции ![]() , вертикальными
прямыми
, вертикальными
прямыми ![]() и
и ![]() и осью
и осью ![]() ,
назовем криволинейной
трапецией.
Рассмотрим
разбиение
отрезка
,
назовем криволинейной
трапецией.
Рассмотрим
разбиение
отрезка ![]() ,
описанное в
предыдущем
пункте, и соответствующую
интегральную
сумму (1). Заметим,
что слагаемые
в (1) равны площадям
прямоугольников
с основаниями
,
описанное в
предыдущем
пункте, и соответствующую
интегральную
сумму (1). Заметим,
что слагаемые
в (1) равны площадям
прямоугольников
с основаниями ![]() и высотами
и высотами ![]() (
(![]() ),
а вся сумма
представляет
площадь ступенчатой
фигуры, образованной
этими прямоугольниками,
см. Рис. 14. Предел
интегральных
сумм (если он
существует),
то есть определенный
интеграл, естественно
принять в качестве
площади криволинейной
трапеции.
),
а вся сумма
представляет
площадь ступенчатой
фигуры, образованной
этими прямоугольниками,
см. Рис. 14. Предел
интегральных
сумм (если он
существует),
то есть определенный
интеграл, естественно
принять в качестве
площади криволинейной
трапеции.
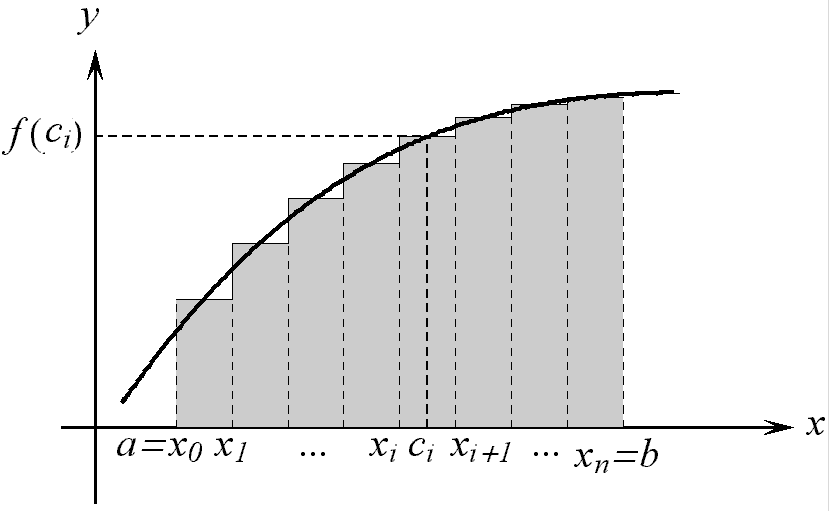
Рис. 14.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
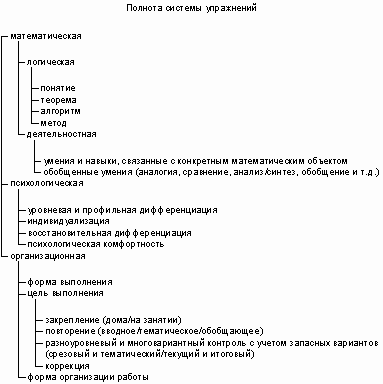
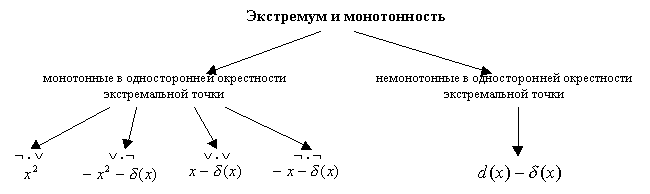
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
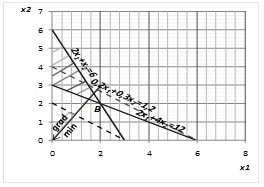
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





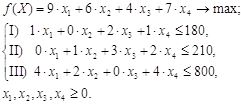
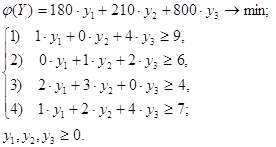
0 комментариев