Навигация
1. Определения
Порядком дифференциального уравнения называется наибольший порядок входящих в него производных. Этот параграф посвящен обыкновенным дифференциальным уравнениям первого порядка, то есть уравнениям вида
![]() ,
,
где ![]() - заданная функция,
- заданная функция,
![]() - независимая
переменная,
- независимая
переменная,
![]() - искомая функция,
- искомая функция,
![]() - ее производная.
Уравнения вида
- ее производная.
Уравнения вида
![]()
называются разрешенными относительно производной.
Функция ![]() называется
решением
дифференциального
уравнения, если
после ее подстановки
уравнение
обращается
в тождество.
Процесс нахождения
решений называется
интегрированием
уравнения.
Решить уравнение
значит найти
все его решения.
называется
решением
дифференциального
уравнения, если
после ее подстановки
уравнение
обращается
в тождество.
Процесс нахождения
решений называется
интегрированием
уравнения.
Решить уравнение
значит найти
все его решения.
Ниже рассматриваются
только уравнения,
разрешенные
относительно
производной.
В простейшем
случае, когда
правая часть
уравнения не
зависит от ![]() ,
то есть уравнение
имеет вид
,
то есть уравнение
имеет вид
![]() ,
,
любое его решение
является
первообразной
функции ![]() ,
а интегрирование
уравнения
сводится к
отысканию
неопределенного
интеграла от
,
а интегрирование
уравнения
сводится к
отысканию
неопределенного
интеграла от
![]() (см. § 4). Совокупность
всех решений,
то есть общее
решение уравнения,
можно представить
формулой
(см. § 4). Совокупность
всех решений,
то есть общее
решение уравнения,
можно представить
формулой
![]() ,
,
где ![]() - произвольная
постоянная.
При этом в данном
параграфе под
неопределенным
интегралом
функции условимся
понимать не
все множество
ее первообразных,
а любую фиксированную
первообразную.
- произвольная
постоянная.
При этом в данном
параграфе под
неопределенным
интегралом
функции условимся
понимать не
все множество
ее первообразных,
а любую фиксированную
первообразную.
Пример. Для уравнения
![]() ,
,
интегрируя, получим общее решение
![]() .
.
В следующем пункте рассматривается один класс уравнений, общее решение которых представляется в квадратурах, то есть с использованием интегралов от известных функций.
2. Уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
![]() , (1)
, (1)
где ![]() и
и ![]() -
заданные функции.
-
заданные функции.
Заметим, что
если для некоторого
значения ![]() выполнено
выполнено ![]() ,
то функция
,
то функция ![]() является решением
уравнения (1).
является решением
уравнения (1).
Рассмотрим
случай ![]() .
Разделив левую
и правую части
уравнения на
.
Разделив левую
и правую части
уравнения на
![]() ,
получим
,
получим ![]() ,
откуда следует
соотношение
между первообразными
,
откуда следует
соотношение
между первообразными
![]() ,
где
,
где ![]() - произвольная
постоянная.
Используя
формулу замены
переменной
в неопределенном
интеграле (см.
§ 4), получаем
равенство
- произвольная
постоянная.
Используя
формулу замены
переменной
в неопределенном
интеграле (см.
§ 4), получаем
равенство
![]() , (2)
, (2)
определяющее в неявном виде семейство решений уравнения (1), зависящее от произвольной постоянной.
Замечание. Чтобы из бесконечного множества решений дифференциального уравнения выделить частное решение нужно задать какое-либо дополнительное условие, например,
![]() , (3)
, (3)
где ![]() ,
,
![]() - некоторые
постоянные.
Условие (2) называется
начальным,
а задача отыскания
решения, удовлетворяющего
такому условию,
называется
задачей Коши.
- некоторые
постоянные.
Условие (2) называется
начальным,
а задача отыскания
решения, удовлетворяющего
такому условию,
называется
задачей Коши.
Пример. Найдем общее решение уравнения
![]() .
.
Используя (2),
получаем ![]() ,
то есть
,
то есть ![]() ,
где
,
где ![]() - произвольная
постоянная.
Отсюда находим
семейство
решений
- произвольная
постоянная.
Отсюда находим
семейство
решений ![]() .
Кроме того,
имеется решение
.
Кроме того,
имеется решение
![]() ,
при котором
правая часть
уравнения
обращается
в ноль. Все найденные
решения можно
представить
одной формулой
,
при котором
правая часть
уравнения
обращается
в ноль. Все найденные
решения можно
представить
одной формулой
![]() ,
,
где ![]() - произвольная
постоянная.
- произвольная
постоянная.
Пример. Рассмотрим уравнение
![]() . (4)
. (4)
Как и в предыдущем
примере, ![]() является решением.
При
является решением.
При ![]() получаем
получаем ![]() или
или ![]() ,
откуда находим
бесконечное
семейство
решений
,
откуда находим
бесконечное
семейство
решений
![]() .
.
Пример. Решим задачу Коши
![]() ,
,
![]() .
.
Заметим, что
функция ![]() удовлетворяет
уравнению, но
не удовлетворяет
начальному
условию. Пусть
удовлетворяет
уравнению, но
не удовлетворяет
начальному
условию. Пусть
![]() ,
тогда общее
решение определяется
из равенства
,
тогда общее
решение определяется
из равенства
![]() ,
откуда
,
откуда 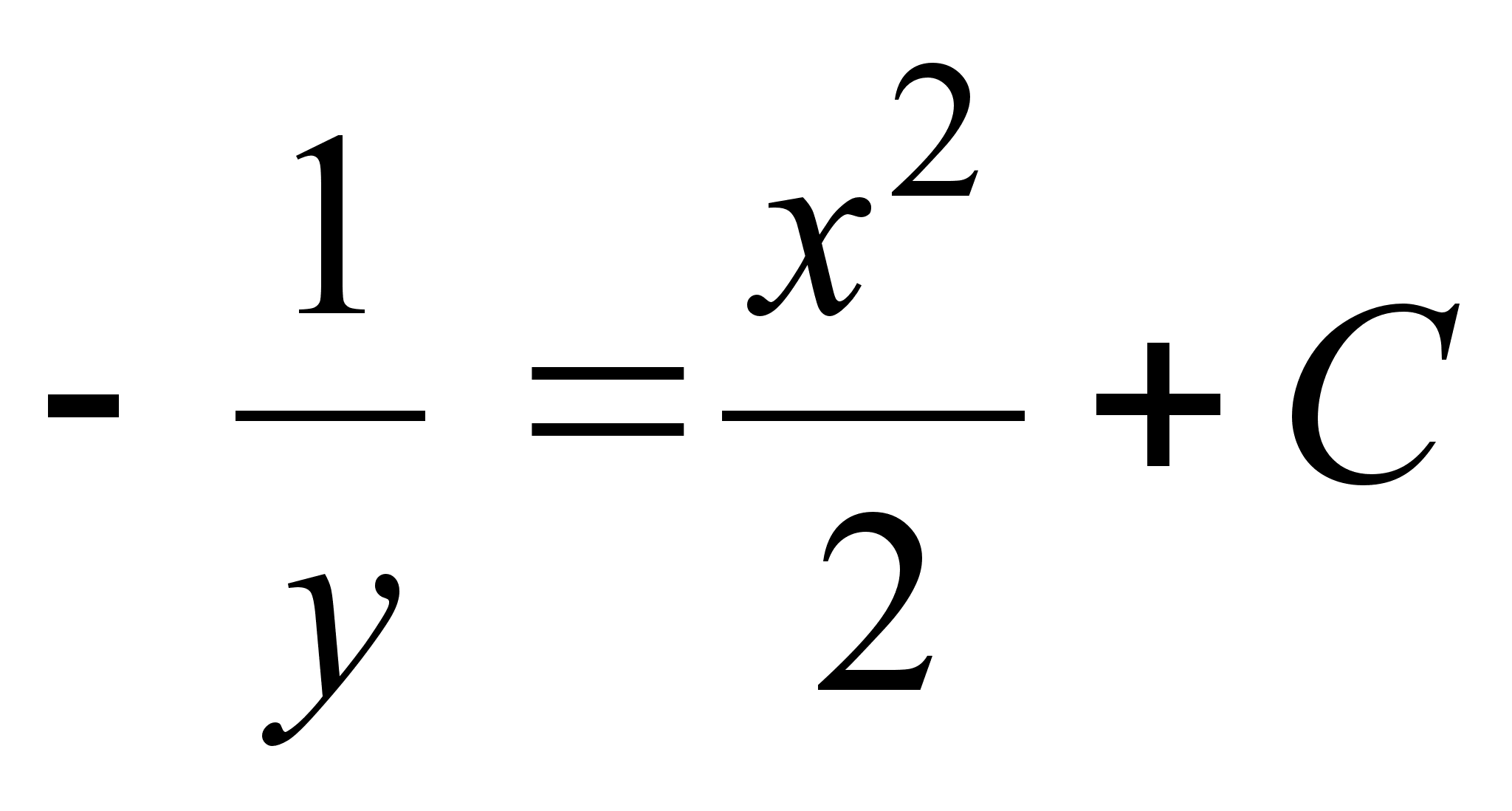 и, следовательно,
и, следовательно,
![]() .
.
При ![]() с учетом начального
условия получим
с учетом начального
условия получим
![]() ,
откуда
,
откуда ![]() .
Таким образом,
решением задачи
Коши является
функция
.
Таким образом,
решением задачи
Коши является
функция
![]() .
.
Похожие работы
... и докажите сходимость полученного разложения к порождающей функции. Исследовать на абсолютную и условную сходимость . Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЙ АНАЛИЗ Билет № 12 Сформулируйте теорему Ролля и объясните ее геометрический смысл. Исследуйте функцию на выпуклость и вогнутость. Какая ...
... «Математических лекциях о методе интеграла»[9]. Здесь дан способ взятия большинства элементарных интегралов и указаны методы решения многих дифференциальных уравнений первого порядка. 2 Вклад Л.Эйлера в развитие математического анализа Леонард Эйлер (Euler, Leonhard) (1707–1783) входит в первую пятерку величайших математиков всех времен и народов. Родился в Базеле (Швейцария) 15 апреля ...
... педагогически значимого подмножества, на основе которого можно было бы провести углубленное изучение понятия экстремума в его взаимосвязях с другими понятиями математического анализа. Во-вторых, объективно получается, что традиционные коллекции упражнений созданы не столько для изучения понятия экстремума, сколько для иллюстрации методов дифференциального исчисления для его отыскания. Этого вполне ...
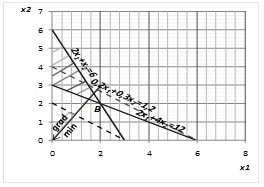
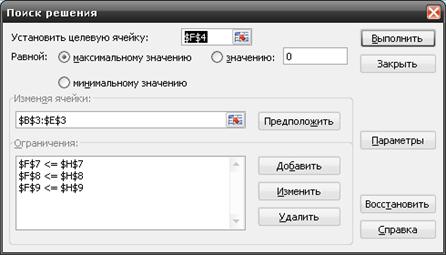
... решений целевая функция принимает в точке (0; 6), и это значение равно . рис. 1 - Графическое решение задачи линейного программирования ЗАДАЧА 2 Использовать аппарат теории двойственности для экономико-математического анализа оптимального плана задачи линейного программирования Для изготовления четырех видов продукции используют три вида сырья. ...





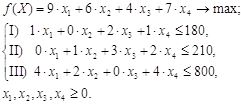
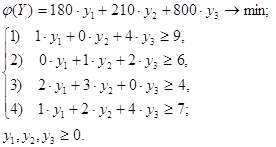
0 комментариев