Основні елементарні функції та їх графіки
Перетворення графіків функцій
Для всіх основних елементарних функцій у довільній точці їх визначення справедлива рівність
Неперервність функції. Дослідження функції на неперервність
Похідна складеної та оберненої функції
Диференціювання неявної функції та функції, заданої параметрично
Логарифмічне диференціювання
Диференціал функції
Монотонність функції. Екстремум функції
Знаходження найбільшого і найменшого значень функції
Навигация
Знаходження найбільшого і найменшого значень функції
Вивчення диференціального числення функцій однієї та багатьох змінних в умовах модульно-рейтингової системи
34055
знаков
1
таблица
17
изображений
3.2 Знаходження найбільшого і найменшого значень функції
Нехай на відрізку
задано неперервну функцію 
, тоді за теоремою Вейєрштрасса функція на даному відрізку досягає свого найбільшого і свого найменшого значень. Це може статися як всередині відрізка, так і на його кінцях. Якщо функція набуває найбільшого значення всередині відрізка, то це найбільше значення є одночасно і один з максимумів (локальний максимум) заданої функції.
Теж саме можна сказати про найменше значення функції. Але може бути й так, що одне із значень функція набуває всередині відрізка, а друге на одному з кінців.
Звідси випливає спосіб знаходження точок, в яких функція набуває найбільшого та найменшого значення на відрізку :
1) знайти критичні точки функції;
2) обчислити значення функції в критичних точках, які належать відрізку, і на кінцях відрізка;
3) найбільше (найменше) значення серед утвореної множини і буде найбільшим (найменшим) значенням функції, заданої на відрізку .
Приклад 1. Знайти найбільше і найменше значення функції 
на відрізку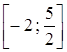 
.
Розв’язання. Знаходимо стаціонарні точки. Для цього знайдемо похідну:
Прирівнюючи цю похідну до нуля і розв’язуючи рівняння
,
дістаємо стаціонарні точки: 
. Точок, в яких функція не існує, немає.
Обчислюємо значення функції в точках 
, а також на кінцях відрізка, тобто в точках 
:
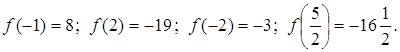
Отже, найбільше значення 
, найменше є 
.
Приклад 2. Знайти найбільше та найменше значення функції 
на відрізку 
.
Розв’язання. Функція є неперервною на відрізку . Знаходимо екстремуми функції. Обчислюємо першу похідну:
.
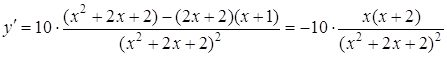Функція має дві критичні точки: 
. Але 
не належить відрізку . В точці 
функція має максимум, причому 
. Обчислюємо значення функції 
на кінцях відрізка: 
.
Таким чином, 
.
Приклад 3. Знайти найбільше та найменше значення функції 
на відрізку 
.
Розв’язання. Знаходимо критичні точки функції, розв’язавши рівняння 
:
.
Коренями цього рівняння є числа: 
. Проте ці точки не належать відрізку , тому всередині цього відрізка критичних точок немає.
Обчислюємо значення функції на кінцях відрізка:
.
Отже, 
.
3.3 Інтервали опуклості та угнутості кривої, точки перегину
Графік функції 
може бути опуклим або угнутим.
Графік функції є опуклим на проміжку 
, якщо відповідна дуга кривої лежить нижче дотичної, проведеної в довільній точці 
.
Графік функції є угнутим на проміжку , якщо відповідна дуга кривої лежить вище дотичної, проведеної в довільній точці .
Для дослідження графіка функції на опуклість застосовується друга похідна функції. Якщо друга похідна двічі диференційовної функції від’ємна 
в інтервалі , тоді графік функції опуклий на даному проміжку, якщо друга похідна додатна 
, тоді графік функції угнутий на .
Точка, при переході через яку крива змінює опуклість на угнутість або навпаки, називається точкою перегину.
Точками перегину функції можуть бути лише точки, в яких друга похідна 
дорівнює нулю або не існує. Такі точки називають критичними точками другого роду.
Похожие работы
... мов полягає в наявності сформованої іншомовної комунікативної компетенції,яка входить до складу когнітивно-технологічного компоненту. 2. Компонентно-стурктурний аналіз професійної компетентності вчителя іноземних мов Професійна компетентність учителя синтезує в собі, по-перше, загальні вимоги до педагога як до особистості, по-друге, особливості його професійно-педагогічної діяльності, по-трет ...
... єнню студентами навчальної програми. Система розрахована на студентів з різним рівнем підготовки і допомагає кожному з них зайняти своє місце у суспільстві та набути високу професійну кваліфікацію. 1.5 Педагогічний процес у ВНЗ МВС Франції Сучасна система вищої освіти Франції, яка склалася в процесі історичного розвитку, нині включає: університети з традиційною системою факультетів і пі ...
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується методика розробки ефективних критеріїв оцінки інноваційних ...
... українського народу. Україна на шляху суверенного розвитку: суспільно-політичні трансформації. Формування політичних партій. “Партія влади” та опозиція, їх вплив на громадсько-політичне життя в Україні. Соціальна політика в контексті нових реалій. Культура, освіта та наука в умовах функціонування суверенної держави. Українська церква та проблеми духовного відродження нації. Партійне життя. ...
0 комментариев