Диференціал функції

2.7 Диференціал функції

 

Диференціал функції, як і похідна, застосовується при розв’язанні ряду практичних задач, зокрема в наближених обчисленнях.

Диференціалом функції  в точці х називається головна (лінійна відносно ) частина приросту  диференційовної в точці х функції.

Диференціал дорівнює добутку похідної функції в точці х на приріст незалежної змінної, тобто

Зокрема, диференціалом незалежної змінної є ії приріст:

Тоді формула диференціала має вигляд

відкіля

Основні властивості диференціала

Для довільних диференційованих функцій  та  мають місце такі рівності:

1. ;

2.  — довільні сталі;

3. ;

4. ;

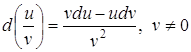5. .

Приклад 1. Знайти диференціал функції .

Розв’язання. За формулою

Приклад 2. Знайти диференціал функції .

Розв’язання. За формулою

Застосування диференціала до наближених обчислень

При малих  справедлива формула , тобто

.

Приклад 1. Обчислити наближено за допомогою диференці-ала значення функції  в точці .

Розв’язання. Найближча к 1,97 точка, в якої легко обчислити значення  и , — це точка .

, .

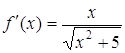За наведеною формулою маємо

Приклад 2. Знайти, наскільки зміниться довжина ребра куба, якщо об’єм його зменшиться з 64 до 63,98 м³.

Розв’язання. Якщо х – об’єм куба, а у – його ребро, тоді

.

За умовою задачі , . Приріст  сторони куба обчислюємо наближено:

,

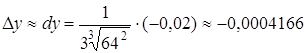тобто ребро куба зменшиться на 0,0004166 м.

2.8 Похідні та диференціали вищих порядків

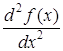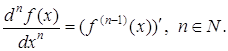
Похідні вищих порядків Похідною другого порядку (другою похідною функції)  у точці х називається похідна від її першої похідної  при умові, що  диференційовна в точці х. Вона позначається такими символами: , , , , . Аналогічно визначається похідна п-го порядку функції , яка має (п-1) похідну в точці х:

Похідну, для якої існує п-а похідна в точці х, називають п разів диференційовною в цій точці.

Основні формули обчислення похідних вищих порядків

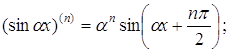
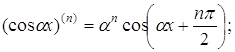
зокрема,

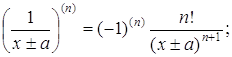
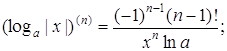
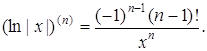
Основні правила обчислення похідних

Якщо функції  та  п разів диференційовні, тоді мають місце такі рівності:

1)

2) 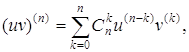 (формула Лейбніца)

де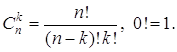

Обчислення похідних вищих порядків функцій, заданих параметрично

Якщо функція задана параметрично рівняннями , , тоді похідні 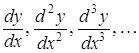 обчислюються за формулами:

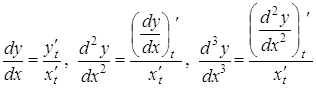 і т.д.

Для похідної другого порядку має місце формула:

Диференціали вищих порядків

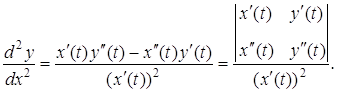
Диференціалом другого порядку двічі диференційовної функції  називають диференціал від диференціала першого порядку функції , тобто . У випадку, коли х – незалежна змінна, диференціали обчислюються за формулами:

Якщо ж х — деяка функція від t, , тоді

 і т.д.

Якщо для функцій  та , х — незалежна змінна, існують диференціали  та , тоді

 ( — сталі),

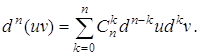
Приклад 1. Знайти похідну другого порядку функції, заданої параметрично

Розв’язання.

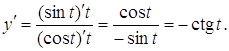
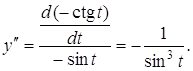
Приклад 2. Знайти похідну другого порядку функції

Розв’язання. Спочатку знаходиться перша похідна від складної функції:

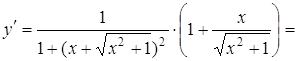
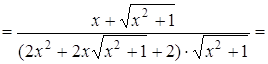
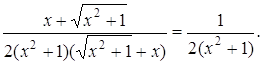
Тоді друга похідна дорівнює:

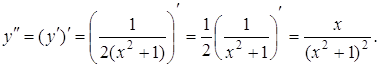
Приклад 3. Знайти диференціал другого порядку функції  в точці .

Розв’язання. Згідно з формулою для обчислення диференці-алу другого порядку  обчислюється :

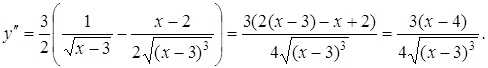
Тоді

Отже,

Приклад 4. Знайти  у випадку, коли функція задана неявно рівнянням

Розв’язання. Диференціюємо ліву та праву частини рівняння, маючи на увазі, що у є функція від х: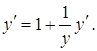

Звідси 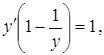 тобто 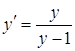, тому

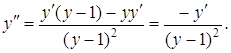
Підставляючи замість  відповідне значення, знаходимо:

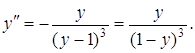
Приклад 5. Знайти  функції, яка задана параметрично рівняннями:

Розв’язання. За правилами диференціювання функції, заданої параметрично, маємо:

 

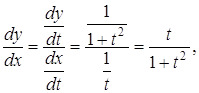
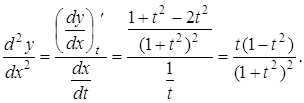
Приклад 6. Знайти , якщо .

Розв’язання. З попереднього прикладу маємо , . Тоді

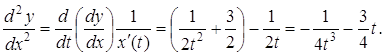
Приклад 7. Знайти , якщо .

Розв’язання.

 

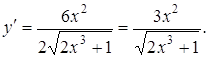
3. Дослідження функції за допомогою похідних