Навигация
Неперервність функції. Дослідження функції на неперервність
1.5 Неперервність функції. Дослідження функції на неперервність
Функція![]() називається неперервною в точці
називається неперервною в точці ![]() , якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці
, якщо існує границя функції в цій точці і вона дорівнює значенню функції в точці ![]() :
:
![]()
Функція ![]() в точці
в точці ![]() буде неперервною тоді і тільки тоді, коли виконуються умови:
буде неперервною тоді і тільки тоді, коли виконуються умови:
1. функція ![]() визначена в околі точки
визначена в околі точки ![]() ;
;
2. існує границя ![]() функції в точці
функції в точці ![]() ;
;
3. границя функції дорівнює значенню функції в цій точці, тобто
![]() (1)
(1)
Разом усі ці умови є необхідними й достатніми для того, щоб функція ![]() була неперервною в точці
була неперервною в точці ![]() .
.
На практиці при дослідженні функцій на неперервність користуються ознаками, які безпосередньо випливають із співвідношення (1), а саме:
для того, щоб функція ![]() була неперервною в точці
була неперервною в точці ![]() , треба щоб:
, треба щоб:
1. ![]() була визначеною в околі точки
була визначеною в околі точки ![]() ;
;
2. існувала лівостороння границя функції в точці, тобто існувало число ![]() ;
;
3. існувала правостороння границя функції – число
![]() ;
;
4. лівостороння й правостороння границя були рівні
![]() =
=![]() ;
;
5. правостороння й лівостороння границя в точці ![]() дорівнювали значенню функції в цій точці, тобто
дорівнювали значенню функції в цій точці, тобто
![]() =
=![]() =
=![]()
Якщо хоч одна с цих умов не виконується в точці, яка є внутрішньою точкою проміжку, в якому визначена функція, то функція в цій точці називається розривною.
Якщо функція ![]() визначена на відрізку
визначена на відрізку ![]() , то в точках а і b можна ставити питання тільки про односторонню неперервність, а саме, в точці а — про неперервність справа, а в точці b — зліва. Тому природно постає питання про введення таких понять, як неперервність функції в точці зліва і справа.
, то в точках а і b можна ставити питання тільки про односторонню неперервність, а саме, в точці а — про неперервність справа, а в точці b — зліва. Тому природно постає питання про введення таких понять, як неперервність функції в точці зліва і справа.
Функція ![]() називається неперервною в точці
називається неперервною в точці ![]() зліва, якщо виконуються умови:
зліва, якщо виконуються умови:
1. ![]() визначена в точці
визначена в точці ![]() (існує число
(існує число ![]() );
);
2. в точці ![]() існує лівостороння границя функції;
існує лівостороння границя функції;
3. лівостороння границя функції дорівнює значенню функції в точці ![]() .
.
Отже, якщо ![]() неперервна в точці
неперервна в точці ![]() зліва, то виконується співвідношення
зліва, то виконується співвідношення
![]() =
=![]() ,
,
де ![]() — лівостороння границя функції в точці
— лівостороння границя функції в точці ![]() .
.
Функція ![]() називається неперервною в точці
називається неперервною в точці ![]() справа, якщо виконуються умови:
справа, якщо виконуються умови:
1. ![]() визначена в точці
визначена в точці ![]() (існує число
(існує число ![]() );
);
2. в точці ![]() існує правостороння границя функції;
існує правостороння границя функції;
3. правостороння границя функції дорівнює значенню функції в точці ![]() .
.
Отже, для неперервної функції справа повинно виконуватися співвідношення
![]() =
=![]() ,
,
де ![]() — правостороння границя функції
— правостороння границя функції ![]() в точці
в точці ![]() .
.
Точкою розриву функції ![]() називають точку
називають точку ![]() в околі якої функція визначена, але в самій точці не задовольняє умові неперервності, що
в околі якої функція визначена, але в самій точці не задовольняє умові неперервності, що ![]() .
.
1. Точка ![]() є точкою усувного розриву, якщо існує
є точкою усувного розриву, якщо існує ![]() , проте
, проте ![]() не визначена в точці
не визначена в точці ![]() , або
, або ![]() . Даний розрив можна усунути, для цього до визначають певним чином функцію в точці
. Даний розрив можна усунути, для цього до визначають певним чином функцію в точці ![]() ;
;
2. Точка ![]() є точкою розриву першого роду, якщо існують скінченні ліва
є точкою розриву першого роду, якщо існують скінченні ліва ![]() та права
та права ![]() границі функції, але
границі функції, але ![]() , різницю
, різницю
![]()
називають стрибком функції ![]() в точці
в точці ![]()
3. Точка ![]() є точкою розриву другого роду функції
є точкою розриву другого роду функції ![]() , якщо в точці
, якщо в точці ![]() не існує принаймні одна з односторонніх границь функції.
не існує принаймні одна з односторонніх границь функції.
Приклад 1. Дослідити точки розриву функції 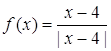 .
.
 Розв’язання. В точці
Розв’язання. В точці ![]() функція не визначена. Знайдемо при
функція не визначена. Знайдемо при ![]() границі даної функції зліва та справа:
границі даної функції зліва та справа:
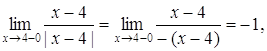
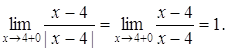
Оскільки односторонні границі скінченні, але
![]() ,
,
то ![]() є точкою розриву першого роду.
є точкою розриву першого роду.
Стрибок в даному випадку в точці ![]() дорівнює 2.
дорівнює 2.
Приклад 2. Дослідити на неперервність функцію ![]()
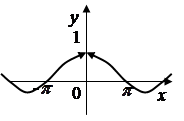 Розв’язання. Дана функція визначена у всіх точках за винятком х = 0. Знайдемо односторонні границі функції в цій точці:
Розв’язання. Дана функція визначена у всіх точках за винятком х = 0. Знайдемо односторонні границі функції в цій точці:
![]()
Рівність ![]() означає, що х = 0 є точкою усувного розриву.
означає, що х = 0 є точкою усувного розриву.
Приклад 3. Визначити характер розриву функції
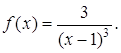
 Розв’язання. Функція в точці
Розв’язання. Функція в точці ![]() не визначена.
не визначена.
При ![]() маємо
маємо ![]() , при
, при ![]()
![]() . Отже,
. Отже, ![]() ,
, ![]() .
.
Тому точка ![]() є точкою розриву другого роду.
є точкою розриву другого роду.
2. Диференціальне числення функції однієї змінної
2.1 Похідна функції в точці ![]()
Похідною функції ![]() в точці х називається границя (як що вона існує) відношення приросту функції
в точці х називається границя (як що вона існує) відношення приросту функції ![]() до приросту аргументу
до приросту аргументу ![]() , коли приріст аргументу прямує до нуля, тобто:
, коли приріст аргументу прямує до нуля, тобто:
![]() . (2.1)
. (2.1)
Функція, яка має скінчену похідну в точці х, називається диференційовною в цій точці. Приріст диференційовної в точці х функції має вигляд
![]() ,
(2.2)
,
(2.2)
де ![]() – нескінченно мала функція при
– нескінченно мала функція при ![]() , тобто диференційовна функція неперервна.
, тобто диференційовна функція неперервна.
Якщо ![]() , тоді функція
, тоді функція ![]() в точці х має нескінченну похідну.
в точці х має нескінченну похідну.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
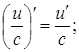 (4)
(4)
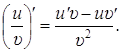 (5)
(5)
Похідні основних елементарних функцій
![]() (6)
(6)
![]() (7)
(7)
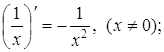 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
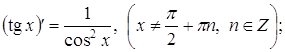 (12)
(12)
![]() (13)
(13)
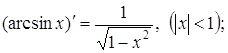 (14)
(14)
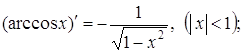 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
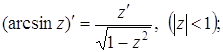 (18)
(18)
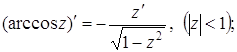 (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Розв’язання. Застосовуючи основні правила диференцію-вання, маємо:
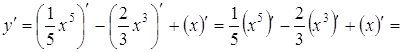
![]()
Приклад 2. Знайти похідну функції ![]() .
.
Розв’язання.
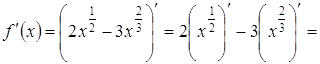
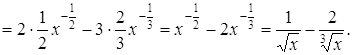
Приклад 3. Знайти похідну функції ![]() .
.
Розв’язання. Використовуючи формули, маємо:
![]()
Приклад 4. Знайти похідну функції ![]() .
.
Розв’язання.
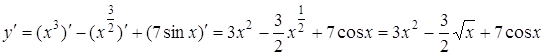 .
.
Приклад 5. Знайти похідну функції ![]() .
.
Розв’язання.
![]() .
.
Приклад 6. Знайти похідну функції ![]() .
.
Розв’язання.
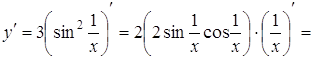
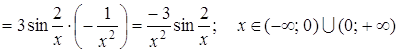 .
.
Приклад 7. Знайти похідну функції ![]() .
.
Розв’язання.
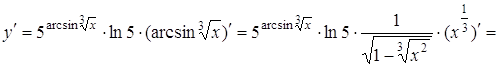
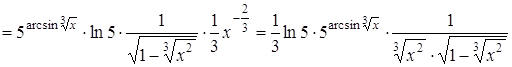 .
.
Похожие работы
... мов полягає в наявності сформованої іншомовної комунікативної компетенції,яка входить до складу когнітивно-технологічного компоненту. 2. Компонентно-стурктурний аналіз професійної компетентності вчителя іноземних мов Професійна компетентність учителя синтезує в собі, по-перше, загальні вимоги до педагога як до особистості, по-друге, особливості його професійно-педагогічної діяльності, по-трет ...
... єнню студентами навчальної програми. Система розрахована на студентів з різним рівнем підготовки і допомагає кожному з них зайняти своє місце у суспільстві та набути високу професійну кваліфікацію. 1.5 Педагогічний процес у ВНЗ МВС Франції Сучасна система вищої освіти Франції, яка склалася в процесі історичного розвитку, нині включає: університети з традиційною системою факультетів і пі ...
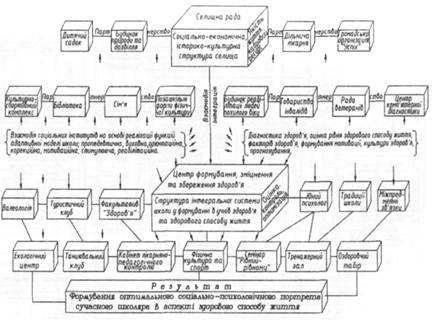
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується методика розробки ефективних критеріїв оцінки інноваційних ...
... українського народу. Україна на шляху суверенного розвитку: суспільно-політичні трансформації. Формування політичних партій. “Партія влади” та опозиція, їх вплив на громадсько-політичне життя в Україні. Соціальна політика в контексті нових реалій. Культура, освіта та наука в умовах функціонування суверенної держави. Українська церква та проблеми духовного відродження нації. Партійне життя. ...

0 комментариев