Монотонність функції. Екстремум функції

3.1 Монотонність функції. Екстремум функції

Припустимо, що функція  визначена на деякому проміжку (а; b), а  є внутрішньою точкою цього проміжку.

Функція  називається зростаючою в точці , якщо існує окіл  точки , який міститься в проміжку (а; b) і такий, що , для всіх  і  для всіх .

Якщо функція  диференційовна на інтервалі (а; b) і зростає (спадає) на цьому інтервалі, то її похідна на інтервалі (а; b) невід’ємна, тобто .

Якщо функція  диференційована на інтервалі (а; b) і ії похідна  для , то ця функція зростає (спадає) на інтервалі (а; b).

Функція  називається спадною в точці , якщо існує окіл  точки , який міститься в проміжку (а; b) і такий, що , для будь якого  і  для будь якого .

Якщо існує окіл  точки , який міститься в проміжку (а; b) і такий, що  для всіх , то точка  називається точкою максимуму функції , а саме число  називається максимумом функції  в точці .

Якщо існує окіл  точки , який міститься в проміжку (а; b) і такий, що  для всіх , то точка  називається точкою мінімуму функції , а саме число  називається мінімумом функції  в точці .

Точки максимуму й мінімуму функції називають ще екстремальними точками, а максимум і мінімум називають екстремумом функції.

Приклад 1. Довести, що функція  є зростаючою в інтервалі .

Розв’язання. Знаходимо похідну функції :

У кожній точці  маємо

Отже, за попередньою теоремою робимо висновок, що функція  є зростаючою в кожній точці даного інтервалу.

Приклад 2. Довести, що показникова функція , , , в інтервалі  при є спадною, а при  — зростаючою.

Розв’язання. Знаходимо похідну функції :

Внаслідок того, що  при , то

Отже, при  функція  є спадною.

Якщо , то  і тому . Таким чином,  у цьому випадку є зростаючою.

Приклад 3. Знайти інтервали зростання і спадання функції:

.

Розв’язання. Знаходимо похідну:

При будь якому  маємо .

Отже, функція  на всій числовій осі  є зростаючою.

Приклад 4. Знайти інтервали зростання і спадання функції:

.

Розв’язання. Знаходимо похідну:

.

При маємо , при  маємо .

Отже, в інтервалі  функція  спадає, а в інтервалі  зростає.

При цьому точка  є точкою мінімуму заданої функції.

Приклад 5. Знайти інтервали зростання і спадання функції:

.

Розв’язання. Знайдемо похідну:

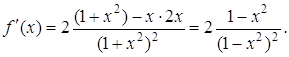
Знайдемо точки, в яких . Це є всі точки, де . Розв’яжемо цю нерівність:

 або .

Отже, в інтервалі  функція зростає. Тоді в інтервалах ,  функція спадає.

Робимо висновок, що точка  є точкою є точкою мінімуму, а точка  — точкою максимуму заданої функції, при цьому мінімум функції дорівнює , максимум .

Якщо функція  у внутрішній точці  проміжку  має екстремум, то в цій точці похідна , якщо вона існує, дорівнює нулю.

Внутрішня точка  проміжку  називається стаціонарною точкою функції , якщо в цій точці . Стаціонарні точки і точки, в яких похідна не існує, називаються критичними точками функції.

Перше правило дослідження функції на екстремум

Щоб дослідити функцію  на екстремум, треба:

1) знайти стаціонарні точки заданої функції, для цього слід розв’язати рівняння , з коренів цього рівняння вибрати тільки дійсні і ті, які є внутрішніми точками існування функції;

2) знайти точки, в яких похідна  не існує (функція  в ціх точках існує). Якщо критичних точок функція  не має, то вона не має й екстремальних точок. Така функція не має екстремуму. Якщо критичні точки є, то їх треба досліджувати далі, для чого:

3) у кожній критичній точці перевірити зміну знака похідної першого порядку.

Якщо  при переході через критичну точку (зліва направо) змінює знак з + на –, то ця точка є точкою максимуму. Якщо  змінює знак з – на +, то ця критична точка є точкою мінімуму.

Якщо при переході через критичну точку знак похідної не змінюється, то розглядувана критична точка не є екстремальною точкою заданою функції.

Теорема. Нехай точка  є стаціонарною для функції  і нехай в цій точці існує похідна другого порядку , яка не дорівнює нулю . Тоді, якщо , то  є точкою мінімуму, якщо , то  є точкою максимуму функції .

Друге правило дослідження функції на екстремум.

Щоб дослідити функцію  на екстремум, треба:

1) знайти стаціонарні точки заданої функції;

2) знайти похідну другого порядку в стаціонарній точці. Якщо в стаціонарній точці  , то  є екстремальною точкою для функції , а саме, точкою мінімуму, якщо , і точкою максимуму, якщо .

Приклад 6. Дослідити функцію на екстремум:

.

Розв’язання. Знаходимо похідну:. Прирівнюємо похідну  до нуля і розв’язуємо рівняння:

Дістаємо стаціонарні точки:

Знаходимо похідну другого порядку:

Підставляємо у вираз для значення  і :

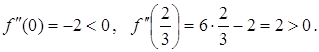
Отже,  є точкою максимуму,  — точкою мінімуму функції , причому максимум і мінімум відповідно дорівнюють .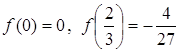

Приклад 7. Дослідити функцію на екстремум:

Розв’язання. Знаходимо похідну першого порядку:

.

Прирівнюємо похідну  до нуля і розв’язуємо утворене рівняння:

.

Звідси знаходимо стаціонарні точки:

Знайдемо похідну другого порядку:

Тоді

Отже, в точці  функція має мінімум , а в точці  — максимум .

Похожие работы

Компетентність вчителя іноземних мов

Скачать

250979

19

4

... мов полягає в наявності сформованої іншомовної комунікативної компетенції,яка входить до складу когнітивно-технологічного компоненту. 2. Компонентно-стурктурний аналіз професійної компетентності вчителя іноземних мов Професійна компетентність учителя синтезує в собі, по-перше, загальні вимоги до педагога як до особистості, по-друге, особливості його професійно-педагогічної діяльності, по-трет ...

Психологічний вплив на педагогічну кваліметнію

Скачать

133248

1

0

... єнню студентами навчальної програми. Система розрахована на студентів з різним рівнем підготовки і допомагає кожному з них зайняти своє місце у суспільстві та набути високу професійну кваліфікацію. 1.5 Педагогічний процес у ВНЗ МВС Франції Сучасна система вищої освіти Франції, яка склалася в процесі історичного розвитку, нині включає: університети з традиційною системою факультетів і пі ...

Взаємодія соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків

Скачать

664560

27

18

... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується ме­тодика розробки ефективних критеріїв оцінки інноваційних ...

Історія України. Соціально-політичні аспекти

Скачать

195443

0

0

... українського народу. Україна на шляху суверенного розвитку: суспільно-політичні трансформації. Формування політичних партій. “Партія влади” та опозиція, їх вплив на громадсько-політичне життя в Україні. Соціальна політика в контексті нових реалій. Культура, освіта та наука в умовах функціонування суверенної держави. Українська церква та проблеми духовного відродження нації. Партійне життя. ...