Логарифмічне диференціювання

2.5 Логарифмічне диференціювання

Якщо маємо громіздкі вирази, що містять добутки, частки, степені, то перш, ніж знаходити похідну, вираз рекомендується прологарифмувати.

Приклад 1. Знайти похідну функції .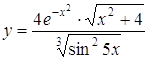

Розв’язання. Прологарифмуємо функцію:

Знайдемо похідну від лівої та правої частин:

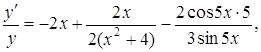
звідки

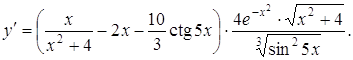
Такий же спосіб використається для знаходження похідної так званої степенево-показникової функції

.

Приклад 2. Продиференціювати функцію:

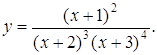
Розв’язання. Цю функцію можна диференціювати як частку двох функцій, але це приведе до складних обчислень. Тому краще спочатку прологарифмувати функцію, а потім продиференціювати.

Дійсно,

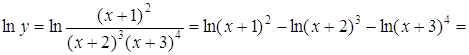
Диференціюючи (у розглядаємо як складену функцію), маємо:

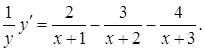
Тоді

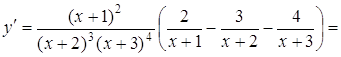
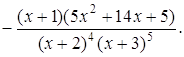
2.6 Геометричний та фізичний зміст похідної

Похідна, особливо її геометричний та фізичний зміст, широко застосовуються при розв’язанні цілого ряду задач в різних галузях діяльності.

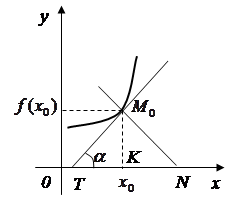Похідна функції  для кожного значення х дорівнює кутовому коефіцієнту дотичної до графіка даної функції у відповідній точці, тобто

,

де  – кут, який утворює дотична до графіка функції в точці  з додатним напрямком осі .

На основі геометричного змісту похідної рівняння дотичної до графіка функції  записується таким чином:

Якщо неперервна функція в точці  має нескінченну похідну, тоді дотичною до графіка функції в точці  буде пряма .

Для нормалі, тобто прямої, що проходить через точку дотику , перпендикулярно до дотичної (пряма ), рівняння має вигляд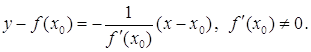

У випадку  нормаллю буде пряма ; якщо функція в точці  має нескінченну похідну, тоді нормаллю до кривої буде пряма .

У деяких задачах потрібно знайти кут  між кривими  та  в їх точці перетинання.

Кутом  між кривими вважається величина кута  між дотичними до даних кривих, в їх точці перетинання;  обчислюється за формулою:

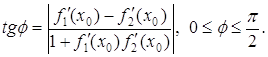
В задачах на застосування геометричного змісту похідної часто зустрічаються також такі поняття, як відрізок дотичної, відрізок нормалі, піддотична, піднормаль, довжини яких визначають за формулами:

а) відрізок дотичної :

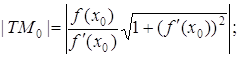
б) відрізок нормалі :

в) піддотична ТК:

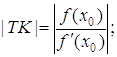
г) піднормаль :

Приклад 1. Знайти, під яким кутом функція  перетинає вісь абсцис.

Розв’язання. Косинусоїда перетинає вісь абсцис в точках . Якщо , тоді

,

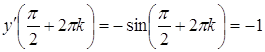тобто кутовий коефіцієнт дотичної до косинусоїди дорівнює –1. Це означає, що в точках  графік функції  перетинає вісь абсцис під кутом .

Якщо , тоді 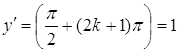. Тому в цих точках косинусоїда перетинає вісь  під кутом .

Приклад 2. Записати рівняння дотичної до кривої

 в точці .

Розв’язання. Згідно з формулою рівняння дотичної до графіку функції, для того, щоб скласти рівняння дотичної, треба обчислити значення функції та похідної функції в точці :

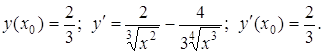
Отже, отримаємо рівняння дотичної:

 або

Приклад 3. Знайти рівняння нормалі до кривої, яка задана параметрично:  в точці .

Розв’язання. Рівняння нормалі має вигляд:

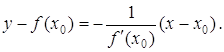
Значення  та  відповідають значенню :

Похідну знайдемо за формулою похідної, заданої параметрично:

.

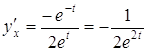В точці  маємо . Таким чином, рівняння нормалі записується у вигляді

, або .

Приклад 4. Знайти рівняння дотичної й нормалі до кривої  у точці .

Розв’язання. Значення похідної даної функції в точці А:

Рівняння дотичної:

Рівняння нормалі:

Фізичний зміст похідної

Під фізичним змістом похідної розуміють швидкість зміни функції в даній точці. Наприклад:

1) при русі тіла швидкість  в даний момент часу  є похідною від шляху :

2) при обертовому русі твердого тіла навколо осі  кутова швидкість  в даний момент часу  є похідною від кута повороту :

3) при охолодженні тіла швидкість охолодження в момент часу  є похідною від температури

4) теплоємність С для даної температури  є похідною від кількості тепла :

5) при нагріванні стержня коефіцієнт лінійного розширення  при даному значенні температури  є похідною від довжини :

Приклад 1. Знайти швидкість точки, рух якої описується рівнянням , наприкінці третьої та десятої секунд.

Розв’язання. Швидкість визначається за формулою

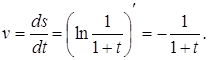
Коли , маємо (м/с).

Коли , маємо (м/с).

Приклад 2. Знайти швидкість точки, яка рухається по колу радіуса , оббігаючи коло за час .

Розв’язання. Нехай точка починає рухатися з положення А проти годинникової стрілки. Нехай за час  вона дійшла до положення .

Кут між її радіусом-вектором та віссю  дорівнює в цей час , тому що точка проходить кут  за час Т, кут  – за одиницю часу і кут  – за час .

Отже, в будь-який момент  положення точки  можна визначити через її дві координати:

Компоненти швидкості знаходимо з таких обчислень:

Тоді швидкість точки буде:

Похожие работы

Компетентність вчителя іноземних мов

Скачать

250979

19

4

... мов полягає в наявності сформованої іншомовної комунікативної компетенції,яка входить до складу когнітивно-технологічного компоненту. 2. Компонентно-стурктурний аналіз професійної компетентності вчителя іноземних мов Професійна компетентність учителя синтезує в собі, по-перше, загальні вимоги до педагога як до особистості, по-друге, особливості його професійно-педагогічної діяльності, по-трет ...

Психологічний вплив на педагогічну кваліметнію

Скачать

133248

1

0

... єнню студентами навчальної програми. Система розрахована на студентів з різним рівнем підготовки і допомагає кожному з них зайняти своє місце у суспільстві та набути високу професійну кваліфікацію. 1.5 Педагогічний процес у ВНЗ МВС Франції Сучасна система вищої освіти Франції, яка склалася в процесі історичного розвитку, нині включає: університети з традиційною системою факультетів і пі ...

Взаємодія соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків

Скачать

664560

27

18

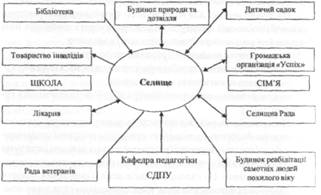
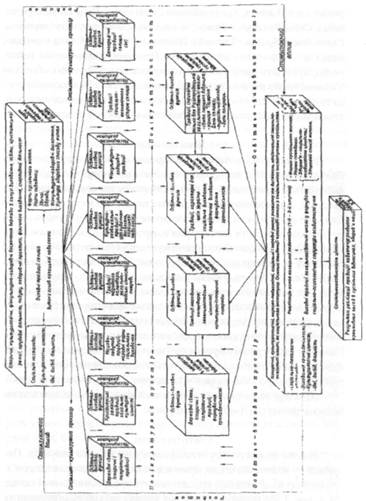
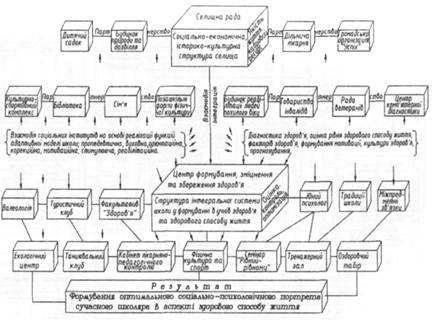
... ів є актуальною, оскільки на її основі реально можна розробити формувальні, розвивальні та оздоровчі структурні компоненти технологічних моделей у цілісній системі взаємодії соціальних інститутів суспільства у формуванні здорового способу життя дітей та підлітків. На основі інформації, яка отримана в результаті діагностики, реалізується ме­тодика розробки ефективних критеріїв оцінки інноваційних ...

Історія України. Соціально-політичні аспекти

Скачать

195443

0

0

... українського народу. Україна на шляху суверенного розвитку: суспільно-політичні трансформації. Формування політичних партій. “Партія влади” та опозиція, їх вплив на громадсько-політичне життя в Україні. Соціальна політика в контексті нових реалій. Культура, освіта та наука в умовах функціонування суверенної держави. Українська церква та проблеми духовного відродження нації. Партійне життя. ...