Необходимое условие локального экстремума функции одной переменной
Нахождение асимптот графиков функции
Теорема о среднем значении для определенного интеграла
Теорема о произвольной от интеграла с переменным верхним пределом
Интегралы с бесконечными пределами
Достаточные условия абсолютного экстермума функции двух переменных
Определенный интеграл. Определение. Геометрический смысл
Вычисление объема и площади поверхности тела вращения с помощью определенного интеграла
Системы линейных уравнений. Правило Крамера
Сложение векторов, умножение вектора на скаляр. Проекция вектора на ось. Коллиниарность и комплиментарность векторов
Смешанное произведение векторов. Его геометрический смысл
Условия || и ^ прямых на плоскости
Парабола
Навигация
Парабола
Шпоры по математическому анализу
56527
знаков
0
таблиц
0
изображений
19. Парабола.
Параболой называется геометрическое место точек плоскости, равноудаленных от данной прямой, называемой директрисой, и от данной точки, не принадлежащей директрисе, называемой фокусом. Обозначим расстояние между фокусом и директрисой через р. Канонической уравнение параболы имеет вид:
у2=2рх и получается, если фокус F поместить в точку (р¸2, 0), а в качестве директрисы взять прямую х = - р¸2. Число р называют параметром параболы, точку (0,0) - ее вершиной.
20. Плоскость в пространстве: общее уравнение, геометрический смысл коэфициентов, уравнение плоскости., проходящей через заданную точку пространства.
Общее уравнение плоскости: Ах+Ву+Сz +D=0, в котором хотя бы один из коэффициентов А,В,С отличен от 0. Эти коэффициенты имеют опред. Геом. смысл
Зададим положение плоскости с помощью некоторой точки М0(х0,у0,z0) и ненулевого вектора N(А,В,С), перпендекулярного плоскости. По этим данным плоскость определяется однозначно. Пусть М(х,у,z) - текущая точка плоскости. Векторы N(А,В,С) и М0М(х-х0,у-у0,z-z0) ортогональны, поэтому их скалярное произведение равно )
А(х-х0)+В(у-у0)+С(z-z0)=0 (1)
После преобразований получаем уравнение:
Ах+Ву+Сz+D=0, где D = -Ах0-В0-Сz0
Следовательно, А,В,С - координаты вектора, перпендекулярного плоскости, заданной общим уравнением.
Множество плоскостей, описываемых уравнением (1), при фиксированной точке (х0,у0,z0) и переменных коэфициентах А,В,С называются связкой плоскостей. Когда среди условий, задающих искомую плоскость, значится ее точка М0(х0,у0,z0), можно начинать решение задачи с применения уравнения (1). Плоскость так же называют поверностью первого порядка.
23. Сфера,
Сфера. Уравнение сферы, центр которой находится в начале координат: х2+у2+z2=R2. Пусть теперь центр расположен в точке М0(х0,у0,z0)
Текущая точка М(х,у,z) сферы находится на расстоянии R от т. М.
Из равенства ММ02=R2 получаем: (х-х0)2+(у-у0)2+(z-z0)2=R2
Эллипсоид канонич. уравнение:
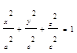- а,в,с - полуоси эллипсоида. При а=в получается эллипсоид вращения. Такую форму имеет поверхность нашей планеты. При а=в=с эллипсоид превращается в сферы радиуса R=а
Параболоид вращения
В плоскости уОz рассмотрим параболу у2=2рz. Поверхность, образованная вращением этой параболы вокруг оси Oz называется параболоидом вращения.
Пусть М(х,у,z) - произвольная точка поверхности, а М0 - точка с той же аппликатой z, лежащая на параболе у2=2рz. Т.к. О'М=О' М0, то у2 для точки М0 можно заменить в уравнении на х2+у2 для точки М: х2+у2=2рz - уравнение параболоида вращения
21. Уравнение прямой линии в пространстве.
Прямую линию в пространстве можно задать как линию пересечения двух непараллельных плоскостей А1х+В1у+С1 z +D1=0 и А2х+В2у+С2 z +D2=0. Рассмотрим случай, когда прямая задана своей точкой М0(х0,у0,z0) и направлением р=(l,m,n). Пусть М(х,у,z) - текущая точка прямой, векторы М0Ми р должны быть коллиниарны, поэтому:
х-х0¸l=у-у0¸m=z-z0¸n (1)
получили каноническое уравнение прямой. Разрешается одной и даже двум величинам в знаминателе обращаться в 0.В этом случае используют свойства пропорции.
х-х0¸l=у-у0¸m=z-z0¸n=t
приравнивая величине t каждое из отношений по отдельности, выразим х, у, z: х= х0+lt, y= у0+mt, z= z0+nt. Получили параметрические уравнения той же прямой.
С помощью (1) можно написать уравнение прямой, проходящей через 2 заданные точки М1(х1,у1,z1) и М2(х2,у2,z2). Одну из этих точек, например М1 можно принять за М0, что даст возможность написать числители в (1). Осталось определить направление прямой. Для этого используют вектор М1М2(х1-х2,у1-у2,z1-z2) его координаты принимают за числа l,m,n В результате приходим к уравнениям:
х-х0¸ х1-х2 =у-у0¸у1-у2=z-z0¸ z1-z2
22. Условия || и ^ прямых на плоскости.
Пусть даны две прямые х-х1¸l1=у-у1¸m1 =z-z1¸n1 и х-х2¸l2=у-у2¸m2 =z-z2¸n2 и две плоскости А1х+В1у+С1z+D1=0 и А2х+В2у+С2z +D2=0. Вспомним, что векторы р1={l1,m1,n1} и р2={l2,m2,n2} имеют направления прямых, а векторы N1{А1,В1,С1} и N2{А2,В2,С2}ортоганальны соответствующим плоскостям. Кроме того, воспользуемся условиями коллиниарности и ортоганальности двух векторов:
1.Условие параллельности прямых.
l1¸l2 =m1¸m2 =n1¸n2
2. Условие параллельности плоскостей
А1¸А2 =В1¸В2 =С1¸С2
3. условие перпендекулярности прямых(скалярное произведение и р1и р2=0)
l1+l2 =m1+m2 =n1+n2=0
4. условие перпендекулярности плоскостей
А1+А2 =В1+В2 =С1+С2=0
4. условие перпендекулярности прямойи плоскости( коллиниарность векторов р1и N1)
l1¸А1 =m1¸В1 =n1¸С1
5. Условие параллельности прямой и плоскости ( ортогонтальность векторов р1и N1)
l1+А1 =m1+В1 =n1+С1=0
Похожие работы
... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...
... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...
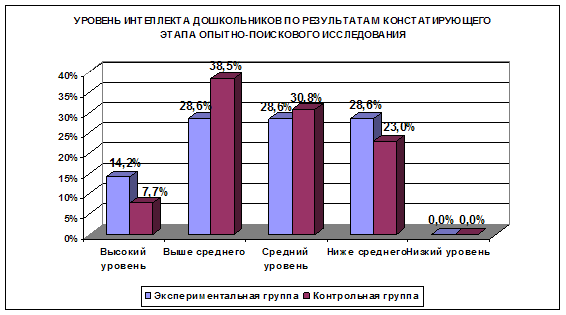
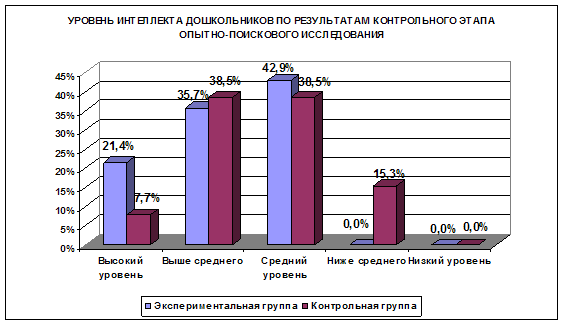
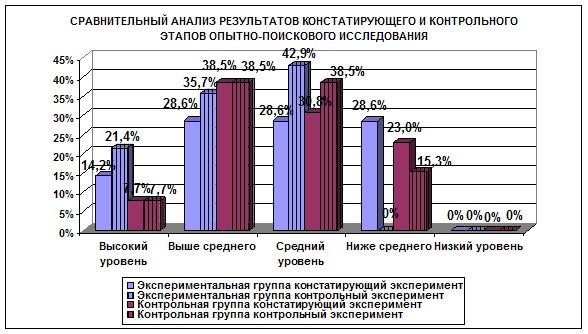
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...
... руководителя. Большое внимание следует уделять мотивации управленческого труда. 56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...
0 комментариев