Сложение векторов, умножение вектора на скаляр. Проекция вектора на ось. Коллиниарность и комплиментарность векторов

7. Сложение векторов, умножение вектора на скаляр. Проекция вектора на ось. Коллиниарность и комплиментарность векторов.

Вектором называется величина, которая характеризуется не только численным значением, но и направлением в пространстве. Модулем |ā| или длиной вектора а наз его числ. зн-ие. Если |ā|=0, вектор называют нулевым..

Проекция вектора на ось.

Пусть в пространстве даны вектор ĀВ и ось Ох. Опустим ^ на ось Ох и з точек А и В, т.е. спроектируем эти точки на ось Ох. Обозначим проекции через А' и В' Вектор A'B' называют компонентой вектора АВ по оси Ох. Проекцией вектора АВ на ось Ох называется длинна компоненты, взятая со знаком "+", если направление оси и компоненты совпадают, и со знаком "-" если направления противоположны.

Сложение и вычитание векторов

Сумма векторов ā и в определяется с помощью параллелограмма. Они выпускаются из одной точки и достраивается параллелограмм. Диагональ этого параллелограмма есть сумма векторов ā и в.

 Сумма векторов так же определяется по правилу многоугольника - к концу первого вектора подставляют начало другого и соединяется начало первого и конец второго.

Разность векторов

с=а-в в+с=а а с

в

Умножение вектора на скаляр.

λ-число (скаляр)

ā - вектор λā=с

Произведением λā называется вектор, длинна которого равна |ā|·|λ|, а направление такое же, как и у вектора ā если λ>0, и противоположное, если λ<0.

Векторы называются коллиниарными, если они лежат на совпадающих прямых.

Если векторы ā и в коллиниарны (ā¹0; в¹0), то они пропорциональны, т.е. существует такое положительное или отрицательное число l, что а=lв.

Три вектора называются компланарными, если их можно уложить на одну плоскость.

9. Скалярное произведение и его свойства.

Скалярным произведением векторов а и в называют произведение их длин и косинуса угла между ними.

(а,b)=|a|×|b|×cos(a,b)

Свойства:

1.     Коммуникативность. (а,в)=(в,а)

2.     Дистрибутивность. (а+в)×(с)=(а×с)+(в×с)

3.     (lа,в)=(а,lв) - скалярный множитель можно выносить за знак скалярного произведения.

4.     Скалярное произведение (а,в) равно 0 тогда и только тогда, когда они ^ или один из них=0

Док-во: cos 90 = 0

8. Длина и направляющие косинусы вектора, заданного координатами. Орты. Радиус-вектор точки.

Векторы единичной длины, направленные по осям координат называют ортами и обозначают i (по оси Ох) j (по оси Оу). В 3х-мерном пространстве берется еще k (по оси z) Проекции а_х  и а_у вектора а на оси х и у называют координатами вектора а. Углы вектора а с осями координат - a и b, тогда а_х =|a|×cosa - направляющие

а_у =|a|×cosb косинусы

a,b - задают направление.

Величины cosa и cosb называются направляющимикосинусами вектора а. Зная координаты а_х и а_у , можно вычислить модуль и направляющие косинусы: cosa= а_х¸|a|, cosb= а_у¸|a|

Очевидно, что |a| = Öа_х² +а_у²

Вектор ОМ, выходящий из (0;0) и оканчивающийся в т. М(х,у) называют радиус-вектором т.М. Координаты х и у т.М. так же являются координатами вектора r=ОМ. Поэтому r=хi+уj. Принято так же писать r ={х,у}

Длина вектора в 3х-мерном пространстве измеряется по формуле

|a|= Ö а_х² +а_у² +а_z²

Векторное произведение и его свойства.

Результатом векторного умножения вектров является вектор. Векторное произведение векторов а и в обозначается так: [а,в] или а´в.

Векторным произведением векторов а и в называется вектор с= [а,в], для кот.:

1.     длина численно равна площади параллелограмма, построенного на этих векторах, т.е. |c|= |a|×|b|×sin(ab)

2.     прямая, несущая вектор, ^ каждому из перемножаемых векторов,т.е. плоскости указанного параллелограмма

3.     направление на этой прямой выбирается так, что бы при взгляде с конца вектора с поворот первого множителя а на наименьший угол до совмещения со вторым множителем в производился бы против часовой стрелки ( такая тройка векторов а,в,с, называется правой)

 Если а и в коллиниарны, то с=0 и вопрос о направлении с отпалдает.

Свойства:

1.     в´а = - а´в, т.е. векторное умножение некоммуникативно

2.     [lа,в]=[а,lв]=l[а,в]

3.     (а+в)´с=а´с+с´в, т.е. векторное умножение дистрибутивно

i j k а_уа_z а_х а_z а_х а_у

а´в= а_ха_уа_z =i в_ув_z - j в_хв_z +k в_хв_у

в_хв_ув_z

Похожие работы

Шпора к канд. минимуму по философии

Скачать

369617

0

0

... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...

История западноевропейской философии

Скачать

161367

0

0

... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...

Развитие интеллектуальных способностей детей средствами математики

Скачать

196174

7

19

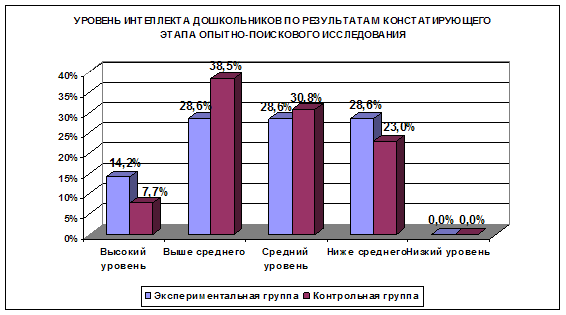
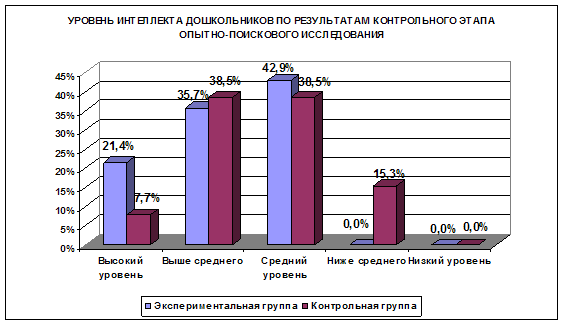
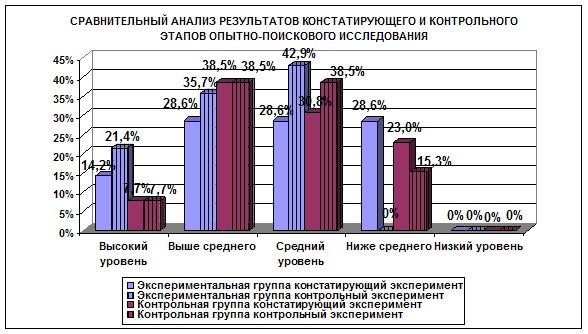
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...

Шпоры по Госам МСХА

Скачать

333055

3

8

... руководителя. Большое внимание следует уделять мотивации управленческого труда.    56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...