Смешанное произведение векторов. Его геометрический смысл

11. Смешанное произведение векторов. Его геометрический смысл.

Под смешанным произведением (векторно-скалярным) векторов а,в,с, понимают число авс=[а,в]×с

Выясним геометрический смысл смешанного произведения. Пусть S=[а,в]

|S|- площадь основания паралл-да

H -высота паралл-да

H= |c| ×|cosj|, где j - острый или тупой угол между векторами S и С.

авс=(s,c)=|s|×|c|×j= |s|×(±H)=±V - объем параллелепипеда.

Знак "+" получается, если тройка а,в,с правая и "-", если леваяÞАбсолютная величина смешанного произведения авс численно равна объему парал-да, построенного на векторах а,в,с.

Исходя из геом. Смысла, получаем необходимое и дополнительное условие компланарности векторов а,в,с, а именно авс=0

Координатная формула величины см. произведения векторов.

а={а_ха_уа_z}, в={в_хв_ув_z}, с={с_хс_ус_z}:

а_ха_уа_z

авс= в_хв_ув_z

с_хс_ус_z

12.Формулы расстояния между двумя точками и длина отрезка в заданном отношении.

Расстояние между точками М₁  и М₂вычисляется как модуль |М₁ М₂| вектора М₁ М_2.

М₁ М₂=| М₁ М₂|=√(х₂ -х₁)² + (у₂ -у₁)²

Нахождение координат точки, делящей отрезок М₁ М₂ в заданном отношении М₁N¸N М₂ = p(число р задано)

Известно ,что || прямые K₁М₁ ;

NL;K₂М₂ рассекают стороны угла M₂AK₂  на пропорциональные отрезки:

p=М₁N¸N М₂=K₁L¸LK₂ или х-х₁¸х₂-х₁=pÞх=х₁+pх₂¸1+p;y=у₁ +pу₂¸1+p

в частности координаты середины отрезка (p=1)

x= х₁ +х₂¸2

у= у₁ +у₂¸2

13. прямая линия на плоскости: общее уравнение, уравнение с угловым коэфициентом, уравнение в отрезках.

Общее уравнение прямой линии - Ах+Ву+С=0, где коэфициенты А, В, С - какие-либо числа, переменные х, у называют текущимикоординатами точки, лежащей на прямой. Некотоорые коэфициенты могут равняться 0, однако хотя бы одно из чисел А, В должно быть отлично от 0, т.е. А²+В²¹0, иначе в уравнении исчезнут обе текущие координаты

у=kх+в - уравнение прямой с угловым коэфициентом

k=tga, где a - меньший из неотрицательных углов, образуемых прямой с положительным направлением оси Ох (0<a<p;a¹p/2)

геом. смысл коэфицтентов

уравнение в отрезках

заданы ненулевые отрезки а и в, отсекаемые прямой на осях координат. По условию точки (а;0) и (0;в) лежат на прямой. Воспользуемся уравнением

х - х₁ у - у₁

^х2^-х1 ^у2^{- у}1

где х₁=а у₁=0

х₂=0 у₂=в

14. Уравнение прямой, проходящей через одну заданную точку, через 2 точки.

у - у₁=k(х - х₁)

уравнение прямой: у=kх+в

Если мы преобразуем первоначальное уравнение у - у₁=k(х - х₁), то получим у=kх+( у₁-kх₁) Оно удовлетворяет условия уравнения прямой : у=kх+в, т.к.

1.     его степень первая, а значит оно может быть прямой,

2.     прямая проходит через точку (х₁; у₁), т.к. координаты этой точки удовлетворяют уравнению : 0=0

3.     роль коэфициента в играет выражение у₁-kх₁

Прямая с уравнением у - у₁=k(х - х₁) проходит через 1 точку. Потребуем, что бы и вторая точка лежала на этой прямой, т.е. что бы выполнялось равенство у₂ - у₁=k(х₂ - х₁). Отсюда находим k= у₂ - у₁¸ х₂ - х₁ и подставим в уравнение:

у - у₁ = у₂ - у₁¸ х₂ - х₁×(х - х₁) или

х - х₁¸х₂ - х₁= у - у₁¸у₂ - у₁

15.Угол м/у прямыми на плоскости

Прямые: у=k₁х +в₁, у=k₂х +в₂

В тр-ке АВС сумма внутр. углов a₁+b равна внешнему углу a₂ поэтому b=a₂-a₁Очевидно, tga₁= k₁; tga₂= k₂.Проименяя формулу для tg разности 2х углов получим tgb=tg(a₂-a₁)= tga₂-tga₁¸1+ tga₂×tga₁

Окончательно имеем tgb= k₂- k₁¸1+k_2××k₁Вычислив тангенс можно найти и сам угол b.

Похожие работы

Шпора к канд. минимуму по философии

Скачать

369617

0

0

... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...

История западноевропейской философии

Скачать

161367

0

0

... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...

Развитие интеллектуальных способностей детей средствами математики

Скачать

196174

7

19

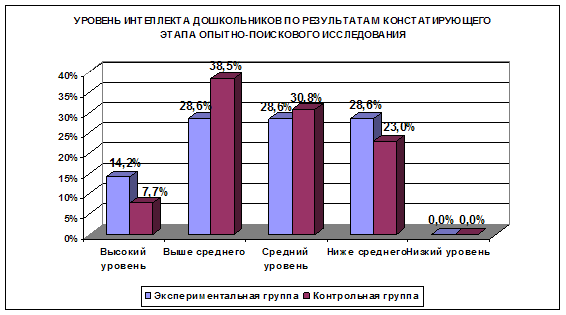
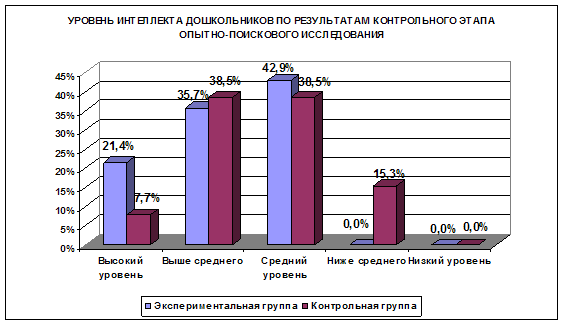
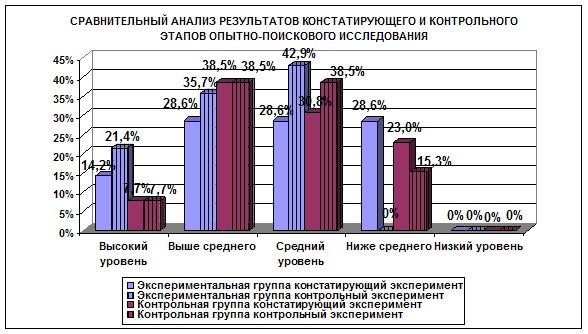
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...

Шпоры по Госам МСХА

Скачать

333055

3

8

... руководителя. Большое внимание следует уделять мотивации управленческого труда.    56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...