Навигация
Определенный интеграл. Определение. Геометрический смысл
19. Определенный интеграл. Определение. Геометрический смысл.
Определение: Пусть дана функция y=f(x), ограниченная на отрезке [a,b] (a<b). Сделаем разбиение R этого отрезка точками хi: а<х0< x1< x2<…< xn,=b. Обозначим
На каждом промежутке [xi, xi+1] выберем произвольную точку ξi. Величину
Называют интегральной суммой.
Если существует предел интегральной суммы sR при λR →0. Независящий от выбора разбиений R и выбора точек ξi, то он называется определенным интегралом от функции f(x) на отрезке [a,b] и обозначается (1)
![]()
Добавление к определению:
1. При a>b полагают
![]()
2. принимают
![]()
В интеграле (1) числа a и b называются соответственно нижними и верхними пределами интегрирования. Если функция f(x) ≥0 на отрезке [a,b], то геометрический смысл определенного интеграла - это площадь криволинейной трапеции. Пусть на промежутке [a,b] задана ограниченная функция y=f(x), будем считать ее положительной.(рис 1)
Фигура aABb, ограниченная графиком функции y=f(x), отрезком [a,b] оси х и перпендикулярами аА и bB к оси х, называется криволинейной трапецией. Измерить ее площадь непосредственно путем установления того, сколько раз в этой фигуре укладывается единица измерения площади (квадрат со стороной, равной единице), и доли этой единицы невозможно из-за криволинейной верхней границы.
Разобьем отрезок [a,b] на части (не обязательно равные) точками хi (i = 0,n): а=х0< x1< x2<…< xn=b. Это разбиение назовем R. Длину наибольшего отрезка назовем
На каждом из частичных отрезков [xi, xi+1] выберем произвольную точку
![]()
И построим прямоугольник с высотой f(ξi). В результате получится ступенчатая фигура, ограниченная сверху ломаной линией L. Ее площадь назовем sR. Если теперь увеличивать число делений разбиения R так, что бы λR →0, то ломаная L будет все теснее прижиматься к кривой АВ. Это дает возможность ввести следующее определние.
Определение: Площадью криволинейной трапеции aAАb называется предел, к которому стремится площадь sR ступенчатой фигуры когда число делений разбиения R не ограничено возрастает и λR →0 (Если этот предел существует и не зависит от способа получения разбиения R и выбора точек ξi).
28. Вычисление площади фигуры и длины дуги с помощью определенного интеграла.
![]()
f(x)≥0
Рассмотрим два случая.
1. площадь S заштрихованной фигуры на рис 1, а, где функция y=f(x) на отдельных промежутках принимает отрицательное значение, выражается формулой:
![]()
2. Площадь S фигуры ограничена графиками функции y=f(x) и y=g(x), а так же прямыми АВ и CD (рис 2) вычисляется по формуле:
Определение: Пусть дана дуга кривой АВ. Нанесем на нее произвольные точки Mi (i=0,n) и соединим их хордами (рис 3). Периметр полученной ломаной обозначим Pn. Будем увеличивать число точек Mi на дуге. Длиной дуги кривой АВ называется предел периметра Pn, когда длина наибольшей хорды стремится к нулю (если этот предел существует и не зависит от выбора вершин ломаной). Если дуга задана уравнением y=f(x) на промежутке [a,b] (ищем длину дуги l). Будем считать функцию f(x) непрерывно дифференцируемой. Положенеи произвольных точек Mi определим выбрав абциссы этих точек, т.е. сделав разбиение R отрезка [a,b] точками а=х0< x1< x2<…< xn=b. Длину хорды, соединяющей точки Mi и Mi+1 обозначим ∆li.Ее проекциями на оси координат будут ∆хi ∆уi. Очевидно,
![]()
Покажем, как нахождение предела периметра Pn сводится к вычислению интеграла. Представим ∆li в нужном виде:
По формуле конечных приращений Лагранжа
![]()
![]()
Поставив это выражение ∆уi в формулу ∆li, полуим
Таким образом (1),
Если составить интегральную сумму для функции
![]()
с полученными выше точками ξi, то придем к выражению (1), т.е.
кроме того стремление к нулю наибольшей хорда ∆li влечет за собой стремление к нулю
поэтому
(если этот предел существует).
![]()
Но по нашим предположениям функция f'(x), а следовательно и функция g(x) непрерывна. Непрерывная функция интегрируема, значит, упомянутый предел существует. Мы доказали, что
Подставляя выражение g(x), получаем формулу длины дуги:
Похожие работы
... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...
... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...
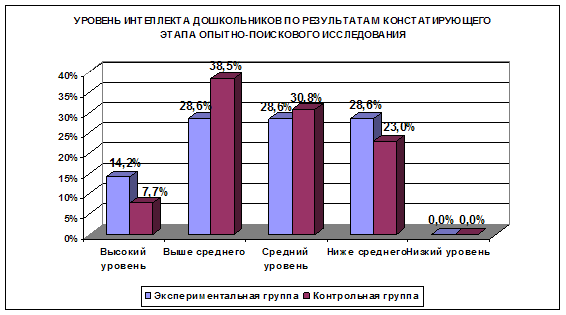
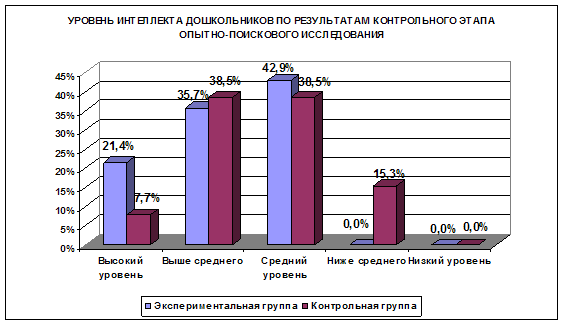
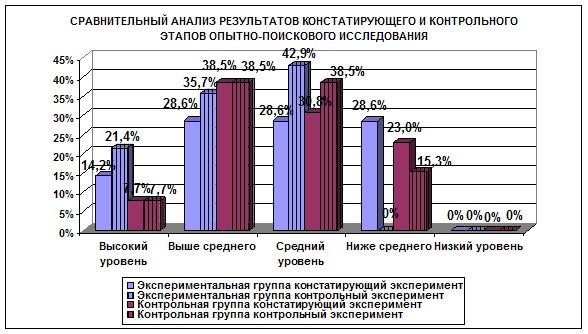
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...
... руководителя. Большое внимание следует уделять мотивации управленческого труда. 56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...



0 комментариев