Навигация
Теорема о среднем значении для определенного интеграла
21. Теорема о среднем значении для определенного интеграла.
Если функция y=f(x) непрерывна на отрезке [a,b], то найдется такая точка ξÎ(a,b), что справедливо равенство:
![]()
Теорема верна и при b<a.
Доказательство: Проведем его для случая a<b. Пусть m и M - наименьшее и наибольшее значение функции f(x) на отрезке [a,b] (для непревной функции они существуют по теореме Вейерштраса). По следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства: (на этом следствие из теоремы закончилось, но к нему относится ниже написанное неравенство))
![]()
можно записать
Поделив это неравенство на полжительное число b-a, получим:
![]()
Непрерывная функция f(x) принимает всякое значение промежуточное между наименьшим m и наибольшим M значениями. Поэтому существует такое число x(a<x<b), что
![]()
Чтд.
22. Классы интегрируемых функций. Функция Дирихле.
интегрируемость не является свойством, присущим всем функциям. В этом убеждает следующий пример. Рассмотрим функцию f(x), называемой функцией Дирихле:
![]()
Сделаем произвольное разбиение R отрезка [a,b]. На любом частичном отрезке [xi, xi+1] найдетсяи как рациональная точка xi. Так, и иррациональная точка hi.Составим две интегральные суммы:sR и
![]()
Пусть
При lR →0 предел интегральных сумм вида :sR равен b-a, в то время, как для
равен нулю. Итак, для интегральных сумм разного вида пределы получаются различные, зависящие от выбора точек на отрезках [xi, xi+1]. Это означает, что функция Дирихле не интегрируемая.
З класса функции:
1. Функции непрерывные на отрезке [a,b].
2. Функции имеющие не более конечного числа разрывов 1-го рода на отрезке [a,b]. (их называют кусочно-непрерывными)
3. Функции монотонные на отрезке [a,b] (у функции этого класса число разрывов может быть бесконечным).
23. Интеграл с переменным верхним пределом. Теорема о его непрерывности.
Теорма: Если функция f(x) интегрируема на отрезке [a,b], то функция
![]()
непрерывна на этом отрезке.
Доказательство: Дадим числу х приращение ∆х так, чтобы х+∆хÎ[a,b]. Для наглядности изобразим на числовой оси один из возможных вариантов расположения точек:
![]()
a x0 x х+∆х b
![]()
Получим:
По теореме (Если функция y=f(x) интегрируема на отрезке, то интегрируема и абсолютная величина |f(x)|, причем
…(на этом теорема закончилась, но неравенство относится к ней.) и следствию из теоремы (Если на отрезке [a,b] функция f(x) интегрируема и удовлетворяет неравенству m£f(x)£M. То выполняются неравенства:
(на этом следствие из теоремы закончилось)
получаем:
![]()
Отсюда следует, что при ∆х→0 будет ∆F→0. Это доказывает непрерывность функции F(x). Отметим, что для подынтегральной функции f(x) точка х может быть точкой разрыва.
Похожие работы
... нельзя быть аморальным политиком. Средство борьбы против этого --- гласность. Ход исторического процесса --- антагонизм. b 10---------- 1. Теоретическое и обыденное сознание. Знание и мнение в древнегреческой философии. Акцент делать на этом вопросе. Общественное сознание - духовная, идеологическая жизнь общества, его мировозрение. Общественное сознание формируется и развивается вместе ...
... . — С 73-77. Лосев А. Ф. Типы античного мышления // Античность как тип культуры. — М., 1988. — С. 78-104. Луканин Р. К. Из истории античного опыта и эксперимента // Филос. науки. — 1991. — № 11. — С. 23-36. Луканин Р. К. Категории Аристотеля в истолковании западноевропейских философов // Путем Октября. — Махачкала, 1990. — С. 84-103. Луканин Р. К. "Среднее"— специфическое понятие аттической ...
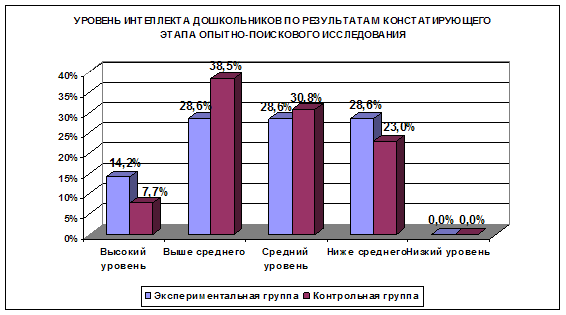
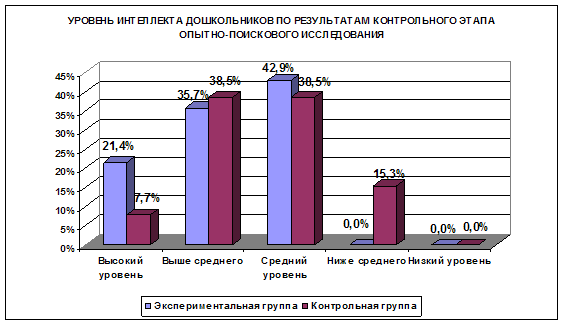
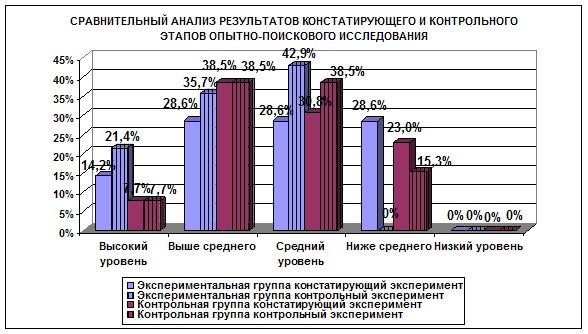
... то целесообразно разработать комплекс заданий по развитию интеллектуальных способностей дошкольников и внедрить его в математический блок программы «Радуга». 2.2 Опытно-поисковые исследования по развитию интеллектуальных способностей средствами математики Для проверки выдвинутой гипотезы провели опытно-поисковые исследования. Опытно-поисковые исследования состояли из трех этапов. На первом ...
... руководителя. Большое внимание следует уделять мотивации управленческого труда. 56. Организационно-распорядительные методы управления (Или административные). С их помощью осуществляются регулирующие функции гос-ва. Основаны на исполнении обязательных предписаний и рекомендаций, позволяют оперативно воздействовать на ход событий в процессе упр-я, ср-во волевого и конкретного воздействия ( ...



0 комментариев