Навигация
Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения
3.2.2. Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения
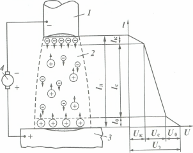
Математическая модель термодеформационного равновесия процесса контактной точечной сварки с обжатием периферийной зоны соединения [210...212], от модели термодеформационного равновесия при традиционных способах КТС, описанной выше, отличается в основном математическим описанием деформационных процессов, протекающих вне контура уплотняющего пояска. Особенности этих процессов, в частности, возможность разделения в процессе формирования соединения контакта деталь–деталь на два отдельных, установлены экспериментально (рис 3.3).

Причиной разделения контакта деталь–деталь являются прогибы ω1 и ω2 свариваемых деталей 3, вследствие увеличения высоты hП уплотняющего пояска между ними в процессе КТС с обжатием периферийной зоны соединения, которое происходит вследствие дилатации и объемных пластических деформаций металла в зоне сварки. В результате из общего контакта деталь–деталь, который формируется при сжатии холодных деталей, образуются два раздельных: свариваемый контакт, который формируется как и при традиционных способах КТС в площади уплотняющего пояска, ограниченного наружным контуром L1t, и замкнутый кольцевой контакт в области сжатия деталей обжимными втулками (с внутренним L2t и наружным L3t контурами). Это возможно в том случае, если внутренний контур обжимных втулок L4 больше контура уплотняющего пояскаL1t, т. е. в том случае, если обжатие осуществляется вне контура уплотняющего пояска.
В рассматриваемой модели процесса формирования соединения, в любой момент времени t, внутри изменяющегося контура уплотняющего пояска L1t протекают те же процессы, что и при традиционных способах КТС. Поэтому напряжения и силы, действующие в зоне формирования соединения и нормальные относительно плоскости свариваемого контакта, обозначим теми же функциями, что и в модели традиционных способов контактной точечной сварки без обжатия периферийной зоны соединений (см. зависимости (3.1)…(3.5)):
- ![]() — напряжения в площади SЭt контакта электрод–деталь;
— напряжения в площади SЭt контакта электрод–деталь;
- ![]() — напряжения в площади SПt свариваемого контакта деталь–деталь;
— напряжения в площади SПt свариваемого контакта деталь–деталь;
- ![]() — распределение электродинамических сил по площади Sjt растекания тока, которые приведены к плоскости контакта и нормальны к ней;
— распределение электродинамических сил по площади Sjt растекания тока, которые приведены к плоскости контакта и нормальны к ней;
- ![]() — распределение давления по площади SЯt ядра в плоскости свариваемого контакта;
— распределение давления по площади SЯt ядра в плоскости свариваемого контакта;
- ![]() — напряжения, возникающее из-за упругой деформации деталей при их сближении до соприкосновения, которые распределены так же по цилиндрической поверхности, но отличающейся тем, что ее направляющей является не контур уплотняющего пояска L1t, а внешний контур L3t кольцевого контакта.
— напряжения, возникающее из-за упругой деформации деталей при их сближении до соприкосновения, которые распределены так же по цилиндрической поверхности, но отличающейся тем, что ее направляющей является не контур уплотняющего пояска L1t, а внешний контур L3t кольцевого контакта.
Применительно к данной модели, пусть распределение нормальных напряжений σ4, относительно плоскости свариваемого контакта, в площади SВt кольцевого контакта обжимная втулка–деталь описывается функцией:
![]() ,
(3.12)
,
(3.12)
а в площади SКt кольцевого контакта деталь–деталь функцией:
![]() .
(3.13)
.
(3.13)
Тогда равновесие элемента замкнутой силовой системы электрод–детали–электрод (одной детали), имеющей при сварке одну степень свободы — перемещение по координате z (ось электродов), в цилиндрической системе координат, аналогично уравнению (3.7), с учетом функций (3.12) и (3.13), описывается следующим интегральным уравнением:
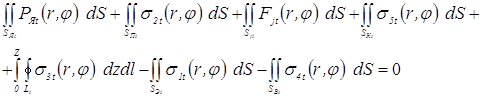 (3.14)
(3.14)
В данной модели параметры термодеформационных процессов внутри контура L1t уплотняющего пояска и вне внешнего контура L3t кольцевого контакта деталь–деталь аналогичны параметрам при традиционном способе сварки. Поэтому 1-ый, 2-ой, 5-ый и 6-ой интегралы в уравнении (3.14) с такими же допущениями, как и в уравнении (3.8): зона сварки осесимметрична, давление расплавленного металла в ядре постоянно по всему объему, вычисляют так же, как и для традиционных способов КТС. Поскольку электродинамические силы отталкивания деталей, как и при обычных условиях КТС незначительны по сравнению с усилием сжатия в свариваемом контакте, то 3-ий интеграл в уравнении (3.14), как и в уравнении (3.8), можно принять равным нулю. Очевидно, что значения 7-го и 4-го интегралов равны усилиям сжатия, распределенным по площадям кольцевых контактов втулка–деталь FОt и деталь–деталь FКt:
![]() , (3.15)
, (3.15)
![]() . (3.16)
. (3.16)
Тогда с учетом сказанного и зависимостей (3.9), (3.10), (3.15) и (3.16) уравнение (3.14) можно преобразовать к форме, аналогичной уравнению (3.11) и удобной для практических расчетов:
![]() . (3.17)
. (3.17)
Здесь, для момента времени t, dЯt и dПt — диаметры, соответственно, ядра расплавленного металла и уплотняющего пояска; PЯt — давление расплавленного металла в ядре; σСРt — среднее значение нормальных напряжении в площади уплотняющего пояска; FДt — усилие, необходимое для сближения свариваемых деталей до соприкосновения их поверхностей; FКt — усилие сжатия деталей в кольцевом контакте; FЭt — усилие сжатия деталей токопроводящими электродами; FОt — усилие обжатия деталей втулками.
Наибольшую практическую ценность представляют решения уравнения (3.17) относительно FЭt и FОt (расчет режимов) при заданных значениях dПt и dВВ, либо относительно dПt (анализ процесса) при заданных значениях FЭt, FОt и dВВ. При этом значения РЯt, dЯt, σСРt и FДt могут быть рассчитаны по тем же методикам, что и в уравнении (3.11).
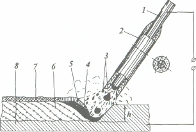
При практических расчетах по уравнению (3.17) усилие FКt, распределенное по площади кольцевого контакта втулка–деталь всегда равно усилию обжатия FОt, которое либо задается, либо рассчитывается как параметр режима сварки. Усилие же, распределенное по площади кольцевого контакта деталь–деталь FКt можно определить из условия равновесия кольцевого элемента детали (рис. 3.4), ограниченного контурами L1t и L3t, которое в интегральной форме можно записать следующим образом:
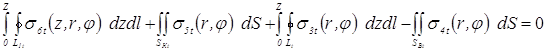 , (3.18)
, (3.18)
где ![]() – распределение напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является контур L1t.
– распределение напряжений по цилиндрической поверхности, образующая которой параллельна оси электродов, а направляющей является контур L1t.

Очевидно, что в уравнении (3.18) 2-ой, 3-ый и 4-ый интегралы при тех же допущениях, аналогичны соответствующим интегралам уравнения (3.14) и равны, как и в (3.17), соответственно, FКt, FДt и FОt.
Точно вычислить 1-ый интеграл в уравнении (3.18) для определения FКt в уравнении (3.17), то есть решить дифференциальное уравнение
С. Жермен-Лагранжа, в настоящее время затруднительно по причинам, описанным в п. 2.1.2. Но если учесть, что температура по ширине уплотняющего пояска изменяется от температуры плавления ТПЛ металла (на границе ядра) до температуры, равной примерно 0,2ТПЛ (на внешнем его контуре), то решение можно упростить. В этом случае можно допустить (поскольку модуль упругости Е → 0), что при упругом прогибе деталей между контурами L1t, и L2t, который происходит вследствие увеличения высоты уплотняющего пояска hПt, металл в области уплотняющего пояска работает как пластический шарнир. Тогда, учитывая изложенное выше и схему воздействия сил на детали, их прогиб между контурами L1t, и L2t приближенно можно рассчитать как деформацию круглой пластинки с отверстием, за которое принимается область внутри контура L1t, жестко закрепленной по внутреннему контуру обжимной втулки L2t, силами σ6t, распределенными по цилиндрической поверхности, направляющей которой является контур L1t. Применяя известное решение этой задачи [213] 1-ый интеграл в уравнении (3.18) определяется следующим выражением:
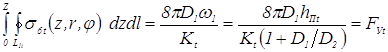 , (3.19)
, (3.19)
где D1 и D2 — цилиндрическая жесткость свариваемых деталей равная:
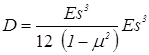 ,
,
причем D1 — меньшая; hПt — высота уплотняющего пояска; Е — модуль упругости; s — толщина детали; μ — коэффициент Пуассона; FУt — сила упругого сопротивления деталей прогибу ![]() ; Kt — коэффициент, равный:
; Kt — коэффициент, равный:
![]()
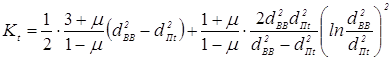 ;
;
dВВ — внутренний диаметр втулки; dПt — диаметр уплотняющего пояска.
Тогда уравнение (3.18) с учетом (3.19) можно преобразовать к виду, удобному для практических расчетов,
![]() . (3.20)
. (3.20)
Относительно диаметра уплотняющего пояска dПt при заданных значениях усилий FЭt и FОt, а также заданном внутреннем диаметре обжимной втулки dВВ, уравнение (3.17), как и уравнение (3.11), решается однозначно. При решении задач по выбору параметров режима (расчет по уравнению (3.17) значений усилий FЭt и FОt и, в случае необходимости, диаметра обжимной втулки dВВ при заданных значениях диаметров уплотняющего пояска dПt) одно и то же усилие в площади свариваемого контакта FCt (в контуре L1t), равное
![]() . (3.21)
. (3.21)
где FЯt и FПt — усилия сжатия в площадях ядра и уплотняющего пояска (см. зависимости (3.9) и (3.10)); может быть получено при различных сочетаниях FЭt и FОt в пределах, обусловленных упругостью деталей (максимальной величины FУt = FУt МАХ). Эта неопределенность устраняется наложением на уравнение (3.17) дополнительных технологических условий, определенных при экспериментальных исследованиях известных способов контактной точечной сварки с обжатием периферийной зоны соединения. Их можно сформулировать следующим образом:
- наиболее оптимальные условия формирования соединения создаются в том случае, если в конце процесса, т. е. при t = tСВ, упругостью деталей FУt, передается в контур уплотняющего пояска L1t 50...100 %, от требуемого условием отсутствия выплеска усилия сжатия в площади уплотняющего пояска FПt;
- величину усилия сжатия в площади кольцевого контакта FКt целесообразно ограничить пределами возможных отклонений усилия в приводах машин для точечной сварки (они не должны превышать 5...10 % от усилия сжатия в контуре уплотняющего пояска FСt [9…11, 14…16, 17...19]), поскольку при FКt > 0 (при соприкосновении деталей в области обжимной втулки) FУt = FУt МАХ, и увеличение усилия обжатия FОt приводит только к увеличению усилия в кольцевом контакте FКt (зависимость (3.20)), без увеличения усилия в контуре уплотняющего пояска FСt.
Оговоренные выше технологические условия, приняв обозначения такими же, как и в уравнениях (3.8) и (3.14), можно выразить следующими зависимостями, в которых отсутствие индекса t указывает на их справедливость только для момента окончания процесса сварки (при t = tСВ):
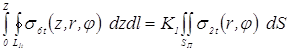 ,
,
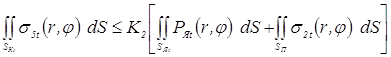 .
.
Эти интегральные выражения после вычисления интегралов с допущениями и граничными условиями, аналогичными уравнению (3.17), можно преобразовать к следующему виду:
![]() или
или ![]() , (3.22)
, (3.22)
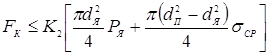 или
или ![]() , (3.23)
, (3.23)
где для момента t = tСВ, FУ – усилие, передаваемое упругостью деталей в контур уплотняющего пояска при t = tСВ; FК – усилие сжатия в площади кольцевого контакта; FС — усилие сжатия деталей в площади свариваемого контакта; К1, К2 — коэффициенты, равные: К1 = 0,5…1, К2 = 0,05…0,1; dЯ, dП, PЯ и σСР — значения dЯt, dПt, PЯt и σСРt при t = tСВ.
Очевидно, что при выполнении условия (3.22) и большой жесткости деталей, либо при уменьшении расстояния между контурами L1t и L2
(dВВ – dПt → 0) наличие кольцевого контакта не является обязательным условием процесса сварки (FКt → 0). В этом случае соприкосновение деталей вне контура уплотняющего пояска может отсутствовать (при FУt МАХ > FОt значение FКt = 0). При этом ![]() (из зависимости (3.20)).
(из зависимости (3.20)).
Из сказанного выше следует, что уравнения (3.8) и (3.11) для традиционных способов сварки являются частным случаем уравнений равновесия (3.14) и (3.17) для КТС с обжатием периферийной зоны соединения, поскольку при dВВ ≤ dПt значение FКt = 0 и если (FЭt + FОt) считать одним усилием, то уравнения (3.14) и (3.17) превращаются, соответственно, в уравнения (3.8) и (3.11). Следовательно, по уравнению (3.17) можно рассчитывать параметры усилия и для обычных условий формирования соединения при традиционных способах КТС. Это позволяет использовать одну и ту же компьютерную программу при расчетах параметров усилия для любых известных способов точечной сварки.
Для практических расчетов по уравнениям термодеформационного равновесия процесса точечной сварки (3.11) или (3.17) необходимо иметь методики определения значений всех их составляющих для любого момента процесса формирования соединения.
Похожие работы
... вредных примесей металла. В заключение раздела отметим, что дуговой разряд, открытый В.Б. Петровым в 1802 г., не исчерпал еще всех своих возможностей и областей применения, включая и область сварочного производства. 3.2 Электрошлаковая сварка Разработка этого принципиально нового процесса была осуществлена в начале 50-х годов прошлого века сотрудниками ИЭС им. Е.О. Патона АН УССР во главе ...
... измерения энергии должна находится в пределах ±(0,1-2,5)%. 4.4 Зависимость погрешности дозирования от состава технических средств комплексов дозирования Поскольку в электротехнические комплексы дозирования помимо рассмотренных выше устройств цифрового дозирования количества электричества и электрической энергии входят также устройства коммутации и датчики тока и напряжения, то необходимо ...
... ? 25. В чем сущность биохимических, фотохимических, радиационно-химических, плазмохимических процессов? Указать области их применения. 26. Какие основные группы физических процессов используют в системах технологий? 27. Дать определение машиностроению как комплексной области. Какова структура машиностроительного предприятия? 28. Раскрыть сущность понятий «изделие», «деталь», «сборочная единица ...
... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...






0 комментариев