Методики определения параметров термодеформационных процессов в условиях формирования точечного сварного соединения

3.5. Методики определения параметров термодеформационных процессов в условиях формирования точечного сварного соединения

Количественное определение сопротивления пластической деформации (СПД) металла в зоне сварки σ_Дt, по-видимому, является наиболее ответственным, так как в основном определяет точность расчётов σ_СРt и Р_Яt по зависимостям (3.51) и (3.59), и сложным элементом при решении технологических задач по уравнениям (3.11) и (3.17) термодеформационного равновесия процессов КТС. В то же время это понятие применительно к условиям точечной сварки в теории КТС является весьма неопределенным. Так, предложенное в работах [3, 80] понятие «условного сопротивления пластической деформации», определяемое как отношение усилия сжатия электродов F_Э к площади контакта деталь–деталь , по сути представляет собой, описанное выше, среднее давление  в свариваемом контакте. Причем определяется оно только экспериментально и не может быть использовано в расчетных методиках

Ниже изложена методика количественного определения сопротивления пластической деформации металла в зоне формирования точечного сварного соединения, которая адаптирована к условиям КТС и позволяет рассчитать его количественные значения в любой момент процесса сварки на стадии нагрева [203, 206, 210, 215… 217].

3.5.1. Сопротивление пластической деформации металла в условиях деформирования при повышенных температурах

Под сопротивлением пластической деформации металла понимается интенсивность напряжений, достаточная для осуществления в теле или его части пластической деформации (ПД) при заданных термомеханических условиях деформирования [221, 226…230].

На величину СПД металла при пластическом деформировании его при высоких температурах, что, в частности, является характерным и для КТС на стадии нагрева, одновременно влияют несколько технологических факторов: температура деформируемого материала, а также степень и скорость деформации. Это обусловлено тем, что в деформируемом металле при температуре выше температуры рекристаллизации Т_РЕКР, которую ориентировочно принимают равной Т_РЕКР ≈ 0,4Т_ПЛ [231], одновременно протекают два противоположных процесса: упрочнение — из-за наклепа зерен, и разупрочнение — из-за их рекристаллизации. Конечный результат зависит от соотношения между скоростью деформации и скоростью рекристаллизации металла [221]. С увеличением температуры СПД металла уменьшается, а пластичность, характеризующая возможную степень ПД без нарушения его сплошности, увеличивается [219, 220].

Упрочнение металла в процессе пластической деформации объясняется увеличением числа дефектов кристаллического строения (дислокаций, вакансий, междоузельных атомов). В частности, связь между пределом текучести σ_Т и плотностью дислокации ρ выражается формулой [232]:

,

где σ₀ — напряжение сдвига при пластической деформации; b — вектор Бюргерса; α — коэффициент, зависящий от типа решетки и состава сплава.

Так, Тейлор и Илом установили, что упрочнение при деформации монокристалла алюминия происходит по параболическому закону [233]:

,

где τ — касательное напряжение в плоскости скольжения; γ — сдвиг.

При увеличении скорости пластической деформации напряжение текучести возрастает, а пластичность падает. С увеличением скорости ПД резко падает пластичность некоторых магниевых сплавов, высоколегированной стали и медных сплавов некоторых марок. Значительно менее чувствительны к скорости деформации большинство алюминиевых сплавов, низколегированные и углеродистые стали [221, 234, 235].

Из определения понятия «сопротивление пластической деформации», общепринятого в теориях пластичности и обработки металлов давлением следует, что оно является характеристикой деформируемого металла, которая зависит от термомеханических условий пластической деформации, а именно: степени ε и скорости u деформации, а так же от температуры деформируемого объема Т_Д [236]. Поэтому оценивать величину СПД в условиях точечной сварки рациональнее не измерением его в ходе процесса КТС, так как осуществить это технически сложно, практически невозможно, а расчетом — с использованием данных и опыта теории и технологии обработки металлов давлением.

Известны ряд эмпирических формул для расчета величины СПД в зависимости от изменения технологических факторов, характеризующих термомеханические условия процесса пластической деформации.

Для определения изменения прочностных характеристик с изменением температуры Т известен ряд зависимостей, в частности, С. И. Губкина [226] для определения временного сопротивления металла σ_В в области температур, составляющих 0,7...1,0 Т_ПЛ:

,

где  — временное сопротивление при температуре 0,95Т_ПЛ и скорости растяжения 40...50 мм/мин; Т_ПЛ — температура плавления сплава (^оС);
α_Т — температурный коэффициент, и зависимость Н. С. Курнакова [237]:

,

где  — значения прочностной характеристики при температуре, соответственно, Т₁ и Т₂; α_Т — температурный коэффициент, постоянный для данного сплава, если в этом интервале температур в нем отсутствуют физико-химические превращения.

Для оценки деформационного упрочнения в процессе пластической деформации известна зависимость [123]:

,

где σ_ист и ε_ист — истинное напряжение и истинная деформация;
А, В и п — постоянные, определяемые экспериментально.

Известен ряд формул, отражающих зависимость деформационных характеристик металла от скорости u его деформирования, в частности, следующие [221, 238]:

П. Людвика — ,

А. Рейто — ,

Е. Зибеля и А. Помпа — ,

А. Надаи — ,

где σ_Д — сопротивление деформации металла; σ_Т — предел текучести при статической деформации; b и т — постоянные коэффициенты, зависящие от материала; σ_S и σ_S0 — напряжения текучести, соответственно, при скоростях деформирования u и u₀; т и п — константы.

Более комплексно реальные процессы упрочнения и релаксации при пластической деформации металла отражены в зависимости, предложенной А. И. Целиковым и В. А. Персианцевым [239], для определения сопротивления деформации σ_Д:

,

где D_У – модуль упрочнения; a_Р – коэффициент, представляющий собой скорость релаксации (c^-1); σ_Т – предел текучести при статической деформации; ε – степень деформации; u – средняя скорость деформации.

Выше приведены лишь наиболее известные решения задачи по определению характеристик металла при их пластическом деформировании. Однако использовать эти формулы применительно к процессу точечной сварки не представляется возможным, поскольку ни одна из них не учитывает одновременного влияния на величину сопротивления пластической деформации основных факторов — температуры, степени и скорости ПД металла, как это имеет место в процессе КТС. Кроме того, для большинства из этих зависимостей не определены значения коэффициентов.

На основании анализа известных методик для определения сопротивления пластической деформации металла и проведенных исследований сделан вывод о том, что для решения поставленной задачи при КТС рационально использовать приближенные, расчетно-экспериментальные методы. В частности, был сделан вывод о том [203, 206, 240], что для определения сопротивления пластической деформации металла в условиях формирования точечного сварного соединения наиболее приемлем метод, предложенный В. И. Зюзиным [241], так называемый «метод термомеханических коэффициентов». По этому методу изменение сопротивления деформации выражается в относительных единицах (коэффициентах) в зависимости от каждого параметра (температуры деформируемого объема Т_Дt, степени ε_t и скорости u_t пластической деформации) в отдельности. Применительно к условиям КТС расчетное значение сопротивления деформации металла σ_Дt определяется по следующей зависимости [203, 206]:

, (3.60)

где σ_0Д — базисное значение сопротивления пластической деформации, при определенных условиях испытаний; к_Тt, к_εt и к_Ut — соответственно, температурный, степенной и скоростной термомеханические коэффициенты в момент времени t.

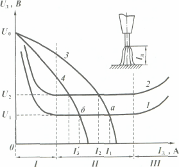
При практическом использовании данного метода определения СПД металла используют значения базисного сопротивления пластической деформации σ_0Д, а также термомеханических коэффициентов: температурного к_Т, степенного к_ε и скоростного к_U, которые определяют экспериментально для разных условий деформирования металла. Их значения представлены в справочной литературе по обработке металлов давлением в виде табличных данных, графиков или аппроксимированных по ним функций. Типичное изменение коэффициентов к_Т, к_ε и к_U в зависимости от изменения соответствующих факторов показан на рис. 3.26.

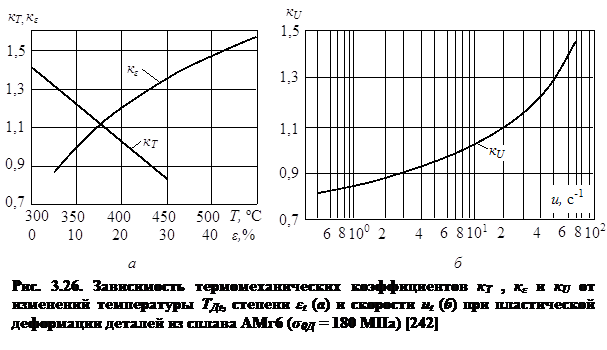
Таким образом, из существующих методов расчетного определения сопротивления пластической деформации металлов, экспериментально-расчетный метод термомеханических коэффициентов является наиболее приемлемым для условий ПД при точечной сварке. Он позволяет учитывать одновременное и комплексное влияние на величину СПД основных факторов процесса пластической деформации металла — температуры, степени и скорости , как это и имеет место в процессе КТС. Кроме того, для наиболее используемых в машиностроении сталей и сплавов определены базисные значения СПД σ_0Д и значения коэффициентов к_Т, к_ε и к_U, которые приведены, например, в работе [242].

Для практических расчетов сопротивления пластической деформации металла по формуле (3.60) в условиях КТС необходимо в любой момент процесса формирования точечного сварного соединения количественно определить степень и скорость деформации, а также температуру деформируемого металла в зоне сварки.

3.5.2 Определение степени и скорости пластической деформации
металла в зоне точечной сварки

По-видимому, в теории точечной сварки понятия степени и скорости пластической деформации металла в зоне формирования соединения определяются не совсем корректно (см. п. 2.5) и математические зависимости для расчёта их параметров не в полной мере отражают сущность этих процессов при КТС и не пригодны для решения практических задач. Ниже описана методика определения степени и скорости деформации в процессе формирования соединения [203, 215, 240], разработанная для условий КТС и вполне приемлемая для решения технологических задач.

В теориях пластичности и обработки металлов давлением, деформацией называют изменение размеров и формы рабочего тела без изменения его массы и объема. При этом, понятие «деформация» относят как к изменению размеров и формы элементарных объемов тела, так и к изменению макроскопических параметров формы и размеров. Количественное определение абсолютной, относительной либо логарифмической (истинной) деформации неизбежно связано с измерением расстояний между точками тела, в том числе и внутри его, поскольку пластическая деформация представляет собой перемещение элементарных объемов тела (точек) относительно друг друга [220, 221, 225, 226]. Однако в условиях точечной сварки сделать это экспериментально с достаточной степенью точности, используя существующие методики (см. п. 2.5.1), не представляется возможным.

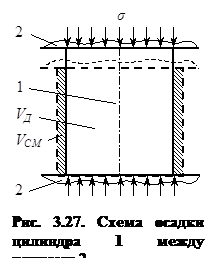
Вместе с тем, в теории обработки металлов давлением известен так называемый «метод определения степени пластической деформации по смещенному объёму». Так, при деформации (осадке) цилиндра объёмом V_Д силами σ (рис. 3.27), которые распределены по его торцевым поверхностям, степень деформации ε, определяемая по смещенному объему V_СМ (заштрихован), равна [221]:

.

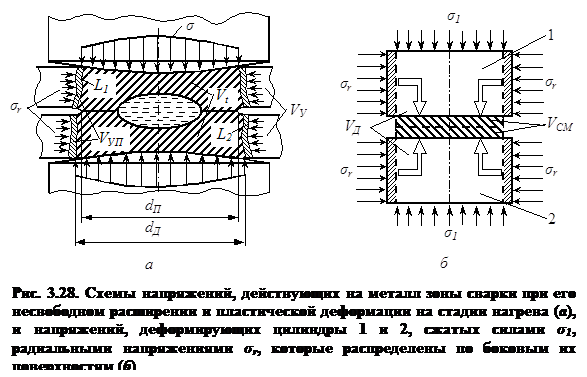
На основании физической модели процессов макропластических деформаций при формировании точечных сварных соединений, которая была сформулирована выше в п. 2.5.2, процесс пластической деформации металла зоны сварки на стадии нагрева может быть уподоблен описанному выше процессу деформации цилиндра при его осадке (рис. 3.28). Это можно сделать на основании результатов экспериментальных исследований пластических деформаций металла в зоне сварки, в частности приведенных в разделе 2.5.2 и в работе [204], если физическую модель (см. рис. 2.32) несколько идеализировать, сделав следующие допущения (рис. 3.28, а):

-    пластические деформации металла при КТС локализованы в объеме металла зоны сварки V_t, ограниченном наружными поверхностями свариваемых деталей и цилиндрической поверхностью, образующей которой является контур L₁, а направляющей — линия, на 10...18 % выходящая за контур уплотняющего пояска:  (см. зависимость (3.58))

-    зона пластических деформаций V_t вне контура L₁ окружена жесткой оболочкой, так как радиальные деформации металла в относительно узком (вследствие большого градиента температуры) поясе V_УП между контурами L₁ и L₂, находящегося в упругопластическом состоянии, а также окружающего холодного металла V_У вне контурами L₁ и L₂, который деформируется только упруго, незначительны и ими можно пренебречь;

-   
осевое пластическое течение (выдавливание) металла, формирующее уплотняющий поясок и являющееся причиной образования вмятин на поверхности электродов, вне контуров контактов деталь–деталь и электрод–деталь отсутствует.

В любой дискретный момент времени t процесса формирования соединения при КТС на цилиндрический пластически деформируемый объем V_t металла зоны сварки, со стороны жесткого кольца V_У холодного металла, который деформируется только упруго, через относительно узкий пояс металла V_УП, находящегося в упругопластическом состоянии, действуют радиальные напряжения σ_r. В результате этого при КТС пластическое течение металла возможно в основном лишь в осевом направлении. Перемещение основного объема деформируемого металла, вследствие наличия осевого градиента температуры, происходит в направлении свариваемого контакта (см. п. 2.5.2). При этом элементарные объемы металла при его пластическом течении в зоне сварки перемещаются так же, как при деформации цилиндров 1 и 2, сжатых силами σ₁, радиальными напряжениями σ_r, которые распределены по боковым их поверхностям (рис. 3.28, б). Таким образом, пластическое течение элементарных объемов металла в зоне сварки при КТС и при деформации цилиндров, напряжениями σ_r, распределенными по боковым их поверхностям, происходит так же, как при описанной выше пластической деформации цилиндра при его осадке (см.
рис. 3.27), но только в обратном направлении.

Степень деформации металла в зоне сварки ε_t, в любой момент времени t процесса формирования соединения при при контактной точечной сварке, на основании сказанного выше (см. рис. 3.28, б) можно определить по зависимости (рис. 3.29):

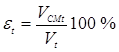, (3.61)

где V_СМt и V_t — смещенный и деформируемый объемы в момент времени t.

Физическая модель процессов макропластических деформаций при формировании точечных сварных соединений (см. п. 2.5.2) и сделанные выше допущения, позволяют определить смещенный объем металла при КТС  (рис. 3.29). В любой момент t процесса формирования точечного сварного соединения смещенный объем металла  равен сумме приращения  деформируемого объема V_t вследствие температурного расширения, включая и нагрев выше температуры плавления в объеме ядра V_Яt, увеличения  объема металла ядра V_Яt при его плавлении, а также объемов металла  и , вытесняемых при вдавливании электродов в детали на глубину c_1t и c_2t:

. (3.62)

Элементарные объемы dV в разных областях зоны сварки, ограниченной контуром L₁, испытывают различное тепловое воздействие, а также претерпевают разные агрегатные превращения. С учетом этого в любой момент t процесса КТС на стадии нагрева приращение  смещенного объема  из-за температурного расширения металла деформируемого объема V_t, и приращение  смещенного объема  из-за увеличения объема металла ядра V_Яt при его плавлении могут быть определены по следующим интегральным зависимостям:

, (3.63)

, (3.64)

где для момента времени t, β_T(Т) — температурный коэффициент объемного расширения; Т(z,r,φ,t) — функция, описывающая изменение температуры в зоне сварки; β^* – коэффициент объемного расширения при плавлении металла, примеры значений которого показаны в табл. 3.3.

Приращения смещенного объема  из-за объемов металла  и , смещаемых при вдавливании электродов в детали, для момента времени t могут быть определены как объемы геометрических фигур по следующим интегральным зависимостям:

, (3.65)

, (3.66)

где для момента времени t,  и  — функции, описывающие геометрию рабочих поверхностей электродов и их положение относительно поверхностей свариваемых деталей; с_1t и с_2t – глубины вдавливания электродов в поверхности деталей; S_1Эt и S_2Эt — площади соответствующих контактов электрод–деталь.

Подставив зависимости (3.63…3.66) в (3.62) получаем интегральное выражение, которое позволяет определить смещенный объем металла V_СМt в любой момент процесса точечной сварки:

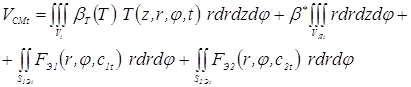. (3.67)

Выразив деформируемый объём V_t интегральной зависимостью

и подставив ее совместно с (3.67) в формулу (3.61), получаем интегральное выражение, которое позволяет определить степень пластической деформации металла в зоне формирования точечного сварного соединения, в любой момент времени t на стадии нагрева [203, 240]:

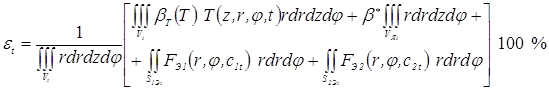. (3.68)

Для точных расчетов степени деформации при конкретных условиях точечной сварки необходимо в интегральную зависимость (3.68) подставить подынтегральные функции. А именно, функции, которые описывали бы изменение в процессе КТС: объема деформируемого металла; изменения в нем температуры; объема расплавленного металла; объема металла, вытесняемого электродами; зависимость температурного коэффициента объёмного расширения от изменения температуры. Кроме того, пределы интегрирования необходимо выразить через функции, которые описывали бы поверхности объема деформируемого металла V_t и объема ядра расплавленного металла V_Яt, а также функции и , описывающие геометрию рабочих поверхностей электродов и их положение в момент времени t относительно поверхностей свариваемых деталей. Учитывая, что вышеназванные функции весьма сложны, а некоторые вообще не определены, то точные аналитические расчеты значений степени пластической деформации по зависимости (3.68) затруднительны, а для решения приближенных технологических задач точечной сварки может быть и не рациональны.

Приближенные технологические расчеты по зависимости (3.68) можно упростить, если кроме допущений, описанных выше, принять и следующие:

-    зона сварки осесимметрична;

-    детали имеют одинаковые теплофизические свойства и одинаковую толщину, т. е. зона сварки симметрична относительно плоскости свариваемого контакта;

-    температурный коэффициент объемного расширения металла β_T не зависит от градиента температуры по координатам и принимается по ее усредненной величине, т. е. ;

-    электроды имеют одинаковую геометрию рабочих поверхностей и вдавливаются в поверхности деталей на одинаковую глубину, т. е.:

,  и .

Тогда, приняв допущения, что зона интенсивных пластических деформаций при КТС ограничена поверхностями деталей в контактах электрод–деталь и цилиндрической поверхностью, образующая которой параллельна оси электродов, а направляющей является контур контакта деталь–деталь, интеграл в зависимости (3.68), который определяет объем деформируемого металла V_t, при толщине деталей s и диаметре уплотняющего пояска d_Пt будет равен:

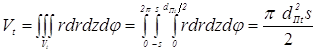. (3.69)

Сделанные допущения, в частности, о том, что температурный коэффициент объемного расширения металла β_T не зависит от температуры, т. е. β_T = const, позволяют упростить вычисление первого тройного интеграла (в квадратных скобках) в зависимости (3.68), который определяет приращения  деформируемого объема металла V_t, вследствие его температурного расширения (зависимость 3.63). Тогда, учитывая, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r и симметрична относительно плоскости свариваемого контакта по координате z, этот интеграл можно преобразовать к следующему виду:

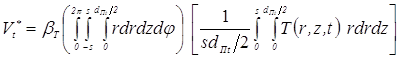. (3.70)

Очевидно, что тройной интеграл в круглых скобках аналогичен зависимости (3.69), а выражение с двойным интегралом в квадратных скобках аналогично зависимости (3.44), если в нее подставить следующие пределы интегрирования: z₁ = 0, z₂ = s, r₁ = 0, r₂ = d_Пt/2. Тогда, с учетом (3.44) и (3.69), а также того, что температурный коэффициент объемного расширения β_T и температурный коэффициент линейного расширения α_T связаны между собой следующим соотношением: β_T = 3α_T [123], зависимость (3.70) можно преобразовать к следующему виду:

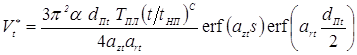.  (3.71)

Допущение об осесимметричности зоны сварки значительно упрощает вычисление и второго тройного интеграла (в квадратных скобках) в зависимости (3.68), который определяет приращение  объема металла ядра при его плавлении. В этом случае объем ядра в любой момент его формирования можно рассчитать как объем тела вращения. Объем ядра V_Яt (рис. 3.30) можно представить как объем тела, ограниченного изотермой температуры плавления, выраженной функцией , при вращении ее вокруг координаты z. Тогда тройной интеграл в зависимостях (3.64) и (3.68) можно преобразовать следующим образом [208]:

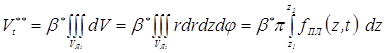, (3.72)

где z₁ и z₂ — координаты точек, в которых изотермы температуры плавления пересекают ось электродов.

Функцию, выражающую зависимость координаты r от координаты z в уравнении изотермы температуры плавления: , можно получить из выражения (3.39). После преобразований эта функция может быть записана в следующем виде:

.

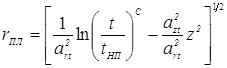Подставив ее в зависимость (3.72) и вычислив интеграл при переменных пределах интегрирования  и , в которых значение высоты ядра h_Яt выражено формулой (3.40), получаем:

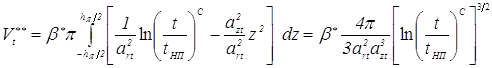. (3.73)

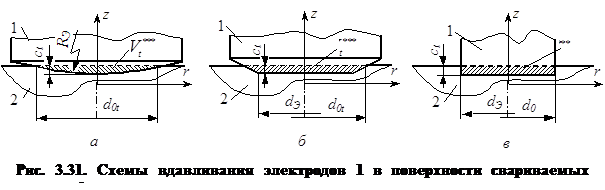
В практике точечной сварки наиболее распространены электроды (рис. 3.31) со сферической рабочей поверхностью (рис. 3.31, а), а также конические (рис. 3.31, б) и цилиндрические (рис. 3.31, в) электродами с плоскими рабочими поверхностями.

Все они являются телами вращения, а потому объемы , вытесняемые электродами при их вдавливании в поверхности деталей, могут быть определены не только по зависимостям (3.65) или (3.66), но и гораздо проще по зависимости (3.72). Однако и в этом нет необходимости, так как общеизвестны формулы, согласно которым вытесняемые объемы равны:

-    при сферической рабочей поверхности электрода

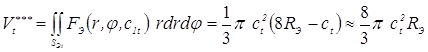, (3.74)

-    при конической форме электрода

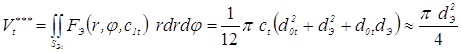 , (3.75)

-    при цилиндрической форме электрода

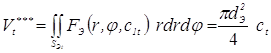, (3.76)

где c_t — глубина вдавливания электродов в момент времени t; R_Э — радиус сферической рабочей поверхности электрода; d_Э — диаметр плоской рабочей поверхности электрода; d_Ot — диаметр отпечатка (контакта) электрод-деталь в момент времени t.

Вторым слагаемым в зависимости (3.74) можно пренебречь потому, что глубина вдавливания электродов при КТС обычно не превышает 10...20 % от толщины s свариваемых деталей, т. е. , а радиусы электродов со сферической рабочей поверхностью , при которых  и практически не влияет на результат расчета объема . По этой же причине можно пренебречь разностью между d_Э и d_Ot в зависимости (3.75), так как при  и , т. е. при , и определять объем  по зависимости (3.76) как при цилиндрическом, так и коническом электродах.

Наиболее сложной задачей при расчетах вытесненного электродами объема  по зависимостям (3.74) и (3.76) является определение глубины вдавливания электродов c_t в процессе формирования соединения. В настоящее время можно прогнозировать лишь качественный характер изменения этого параметра. Определить же значения c_t расчетным путем в процессе КТС с учетом напряженно-деформированного состояния металла области зоны сварки, прилегающей к электроду, пока не удается из-за сложности протекающих там термодеформационных процессов. Поэтому в данной методике значения c_t приближенно определяются через диаметр контакта электрод–деталь. С точностью до 0,01 % значения c_t можно выразить через диаметр отпечатка d_о (контакта электрод–деталь) при сварке электродами со сферическими рабочими поверхностями [84]: .

Экспериментальные исследования показали, что диаметр d_Эt контакта электрод–деталь при точечной сварке изменяется подобно изменению диаметра d_Пt контакта деталь–деталь (рис.3.32). При этом установлено, что в начале процесса КТС d_Эt, на 5...15 % больше d_Пt, а в конце процесса — наоборот, d_Пt примерно на столько же больше, чем d_Эt. Поэтому, для приближенных расчетов можно принять, что d_Эt и d_Пt изменяются при сварке одинаково. Тогда изменение значений глубины вмятин от электродов в поверхностях деталей c_t в процессе сварки электродами со сферической рабочей поверхностью при расчетах вытесняемого ими объема металла  по зависимости (3.74) можно выразить через изменение диаметра уплотняющего пояска следующим образом:

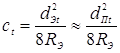. (3.77)

Практика сварки электродами со сферической и плоской рабочими поверхностями показывает, что при сварке на режимах близких к оптимальным, например, рекомендованных в работах [3, 9, 11, 15...17], глубина их вдавливания в поверхности деталей в процессе формирования соединения изменяется примерно одинаково. Поэтому, при приближенных технологических расчетах значений  по зависимости (3.76) величину c_t можно определять по зависимости (3.77) и для условий сварки электродами с плоской рабочей поверхностью, если подставить фиктивное значение R_Э, рекомендованное для этой же толщины деталей, например, в работах [3, 11, 16].

Тогда зависимость (3.68) для расчета степени пластической деформации металла в зоне сварки ε_t в любой момент t процесса формирования соединения на стадии нагрева с учетом сказанного выше и зависимостей (3.71), (3.73) и (3.77) можно преобразовать к следующему окончательному виду, удобному для практических расчетов [210, 217]:

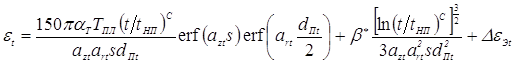 (%), (3.78)

где для момента времени t, α_Т — температурный коэффициент линейного расширения; a_zt, a_rt и с — коэффициенты (см. зависимость 3.36); t_НП — время начала плавления металла (см. зависимость 3.37);  — функция ошибок (см. зависимость (3.42)... (3.44)); s — толщина деталей; d_Пt — диаметр уплотняющего пояска; β^* — коэффициент увеличения объема металла ядра при его плавлении;  — приращение степени пластической деформации ε_t металла зоны сварки при вдавливании электродов, равное:

при сферической рабочей поверхности электрода

,

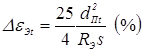при конической и цилиндрической форме электрода

;

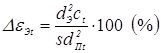R_Э и d_Э – радиус (при сферической) и диаметр (при плоской) рабочих поверхностей электродов; с_t — глубина вдавливания электродов в поверхности деталей (см. зависимость 3.77).

Таким образом, зависимость (3.78) позволяет при технологических расчетах приближенно определить степень пластической деформации ε_t металла в процессе формирования точечного сварного соединения в любой его момент t на стадии нагрева.

Скорость деформации, как это общепринято в теориях пластичности и обработки металлов давлением — это изменение степени деформации ε_t в единицу времени [220, 221, 227,228], т. е.:

. (3.79)

Размерность скорости деформации зависит от размерности ее степени и может быть  или : .

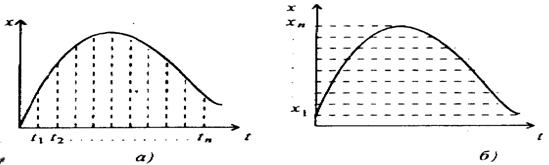
В соответствии с выражением (3.79) скорость деформации можно определить как производную от функции, описывающей изменение по времени степени пластической деформации металла зоны сварки, т. е. производную от зависимости (3.78). Однако в связи с тем, что она содержит не дифференцируемую аналитически erf – функцию, то точное аналитическое определение скорости деформации по (3.79) невозможно. Даже при приближенном дифференцировании функции  [216] получается очень громоздкая и неудобная для практических расчетов зависимость скорости деформации от времени. Поэтому скорость деформации u_t для любого момента t процесса сварки рациональнее определять численным дифференцированием зависимости (3.78) , т. е. [210, 217]:

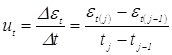, (3.80)

где Δε_t — приращение степени деформации за отрезок времени между текущим и предыдущим  моментами расчета скорости деформации .

3.5.3. Определение температуры металла в зоне пластических
деформаций

Методика, по которой рассчитывается изменение сопротивления пластической деформации металла при КТС, предопределяет осреднение температуры в объеме металла зоны интенсивных пластических деформаций. Рассчитать среднюю температуру металла пластически деформируемого в зоне сварки можно по зависимости (3.44).

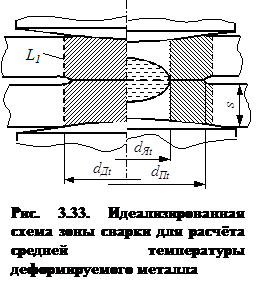
В разделе 2.5.2 экспериментально определено, что пластические деформации металла зоны сварки на стадии нагрева в основном локализованы в области, ограниченной контуром L₁, диаметр которого d_Дt на 5...15 % больше диаметра d_Пt уплотняющего пояска, т. е.  
(рис. 3.33). При расчете же давления в ядре радиус внешней границы металла, находящегося в пластическом состоянии, определен и теоретически. Из зависимостей (3.58) и (3.59) получаем: . Поскольку эти результаты приближенно равны, при расчете средней температуры внешней границей зоны интенсивных пластических деформаций рационально принять окружность диаметром . Внутренней же границей пластических деформаций до начала плавления металла является ось электродов (рис. 3.33, слева), а после появления ядра расплавленного металла (рис. 3.33, справа) — окружность с диаметром d_Яt. Поскольку приняты допущения, что зона интенсивных пластических деформаций при КТС осесимметрична по координате r и симметрична относительно плоскости свариваемого контакта по координате z, то среднюю температуру деформируемого металла можно определять только в одной четверти зоны точечной сварки. Следовательно, для определения Т_Дt по зависимости (3.44) в нее следует подставить следующие пределы интегрирования: , , , .

После подстановки этих пределов интегрирования, вычисления интегралов и преобразований по зависимости (3.44) получаем формулу для расчета средней температуры деформируемого в зоне сварки металла Т_Дt в любой момент t процесса формирования точечного сварного соединения при  [210, 217]:

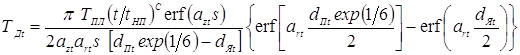, (3.81)

где для момента времени t, Т_ПЛ — температура плавления свариваемого металла; t_НП — время начала плавления металла (см. зависимость 3.37);
a_zt, a_rt и с — коэффициенты (см. зависимость 3.36);  — функция ошибок (см. зависимость (3.42)... (3.44)); s — толщина деталей; d_Яt и d_Пt — диаметры ядра и уплотняющего пояска соответственно.

3.5.4. Определение высоты уплотняющего пояска в свариваемом
контакте

Для решения технологических задач точечной сварки с обжатием периферийной зоны соединений по уравнению (3.17) в любой момент процесса формирования соединения необходимо определять высоту уплотняющего пояска h_Пt (рис. 3.34), которая входит в зависимость (3.19).

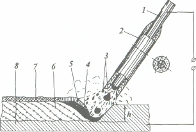
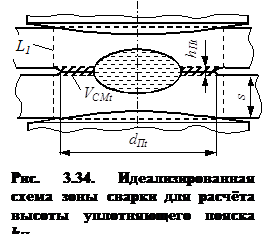В процессе формирования точечного сварного соединения происходит пластическое течение металла в зоне сварки к контакту деталь – деталь вследствие его температурного расширения, увеличения объема при расплавлении в ядре, неравномерного нагрева и сложного объемного напряженного состояния (см. п. 2.5.2). Как показано выше в п. 3.5.2, при пластической деформации металла в зоне сварки к контакту между деталями смещается объём V_СМt в результате чего между свариваемыми деталями образуется рельеф (уплотняющий поясок) высотой h_Пt. Поскольку считается, что металл при пластической деформации не сжимается [200, 219...221, 224...230], высоту уплотняющего пояска h_Пt в любой момент t процесса формирования соединения можно определить следующим образом:

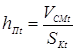,  (3.82)

где в момент времени t, V_СМt — объем металла зоны сварки, смещенный к свариваемому контакту; S_Кt — площадь контакта деталь–деталь.

Изменение смещённого объёма V_СМt в процессе точечной сварки описывается интегральным выражением (3.67). Тогда, выразив площадь контакта деталь–деталь S_Кt интегральной зависимостью

(3.83)

и подставив ее совместно с зависимостью (3.67) в формулу (3.82) получаем интегральное выражение, которое позволяет в любой момент времени t на стадии нагрева определить высоту уплотняющего пояска h_Пt, [204, 210]:

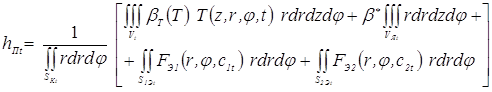, (3.84)

где обозначения полностью соответствуют зависимости (3.67).

Точные аналитические расчеты по зависимости (3.84) затруднительны, а для решения технологических задач может быть и не рациональны, по тем же причинам, что и зависимости (3.68). При допущениях же, которые были сделаны для зависимости (3.68), в частности, об осесимметричности зоны сварки и о ее симметричности относительно плоскости свариваемого контакта, по зависимости (3.82) можно производить приближённые технологические расчёты. В этом случае, вычислив интеграл в (3.83)

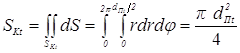(3.85)

и подставив его, совместно с зависимостями (3.70)…(3.77), в выражение (3.84) после преобразований получаем формулу для расчетов высоты уплотняющего пояска в любой момент t процесса формирования соединения при сварке деталей одинаковой толщины [204, 243]:

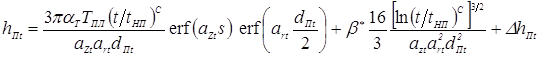, (3.84)

где для момента времени t, α_Т — температурный коэффициент линейного расширения; Т_ПЛ — температура плавления свариваемого металла;
t_НП — время начала плавления металла (см. зависимость 3.37); a_zt, a_rt и с — коэффициенты (см. зависимость 3.36);  — функция ошибок (см. зависимость (3.42)...(3.44)); s — толщина деталей; d_Пt — диаметр уплотняющего пояска; β^* — коэффициент увеличения объема металла ядра при его плавлении;  — приращение высоты уплотняющего пояска h_Пt за счет вдавливания электродов, равное:

при сферической рабочей поверхности электрода

,

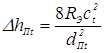при конической и цилиндрической форме электрода

;

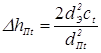R_Э и d_Э – радиус (при сферической) и диаметр (при плоской) рабочих поверхностей электродов; с_t — глубина вдавливания электродов в поверхности деталей (см. зависимость 3.77).

Таким образом, описанные выше методики расчетного определения степени и скорости пластической деформации, температуры металла в зоне сварки, сопротивления его пластической деформации, а также изменения высоты уплотняющего пояска при формировании сварного соединения, позволяют проводить практические расчёты по уравнениям термодеформационного равновесия процессов сварки (3.11) и (3.17), как для традиционных способов сварки, так и для способов сварки с обжатием периферийной зоны соединений.

4. Математическое моделирование процессов
формирования точечных сварных соединений

Общеизвестно то, что величина (степень) объемной пластической деформации в зоне сварки значимо влияет на процесс нагрева, так как определяет плотность тока через площади ее сечений в плоскостях контактов деталь–деталь и электрод–деталь. Вместе с тем, общеизвестно и то, что нагрев металла в зоне формирования соединения, в свою очередь, тоже оказывает влияние на его пластическую деформацию, поскольку влияет на изменение его сопротивления пластической деформации. Таким образом осуществляется как бы саморегулирование процесса точечной сварки. Это предполагает, что при устойчивом процессе формирования соединения в зоне сварки должно существовать определенное соответствие между нагревом в ней металла и пластической его деформацией [3, 165, 185… 187], которое количественно характеризуется критерием жесткости режимов контактной точечной сварки [3, 15].

Однако указанные выше известные гипотезы и предположения лишь качественно определяют возможные взаимосвязи между основными термодеформационными процессами точечной сварки. Описанные же выше математические модели основных термодеформационных процессов, протекающих при КТС, позволяют количественно определить параметры основных термодеформационных процессов в зоне сварки и закономерности их изменений. Это, в частности, можно сделать при решении интегральных уравнений термодеформационного равновесия процессов контактной точечной сварки относительно диаметра уплотняющего пояска. Кроме того, решение этой задачи предопределяет необходимость расчетного определения параметров всех основных термодеформационных процессов, протекающих в зоне сварки.

Таким образом, решение уравнений (3.11) или (3.17) термодеформационного равновесия процесса контактной точечной сварки относительно диаметра уплотняющего пояска фактически позволяют моделировать процесс КТС. Возможность же варьировать при этом параметры режимов сварки фактически предопределяет возможность проведения численных экспериментов.

Похожие работы

История и развитие сварочного производства

Скачать

145500

0

19

... вредных примесей металла. В заключение раздела отметим, что дуговой разряд, открытый В.Б. Петровым в 1802 г., не исчерпал еще всех своих возможностей и областей применения, включая и область сварочного производства. 3.2 Электрошлаковая сварка Разработка этого принципиально нового процесса была осуществлена в начале 50-х годов прошлого века сотрудниками ИЭС им. Е.О. Патона АН УССР во главе ...

Средства учета количества электричества и электрической энергии

Скачать

145927

16

16

... измерения энергии должна находится в пределах ±(0,1-2,5)%. 4.4 Зависимость погрешности дозирования от состава технических средств комплексов дозирования Поскольку в электротехнические комплексы дозирования помимо рассмотренных выше устройств цифрового дозирования количества электричества и электрической энергии входят также устройства коммутации и датчики тока и напряжения, то необходимо ...

Системы технологий

Скачать

259162

24

61

... ? 25. В чем сущность биохимических, фотохимических, радиационно-химических, плазмохимических процессов? Указать области их применения. 26. Какие основные группы физических процессов используют в системах технологий? 27. Дать определение машиностроению как комплексной области. Какова структура машиностроительного предприятия? 28. Раскрыть сущность понятий «изделие», «деталь», «сборочная единица ...

Технология обработки конструкционных материалов

Скачать

305550

1

104

... - дальнейшее развитие, совершенствование и разработка новых технологических методов обработки заготовок деталей машин, применение новых конструкционных материалов и повышение качества обработки деталей машин. Наряду с обработкой резанием применяют методы обработки пластическим деформированием, с использованием химической, электрической, световой, лучевой и других видов энергии. Классификация ...